Analog-to-digital convertor (ADC) as an important part of communication system needs to satisfy the requirements of the rapid development of ultra-wide-band applications such as advanced Radar communication system, high speed optical communication, etc.^{[1– 4]} The electrical ADC whose sample rate and art resolution are several giga-samples per second (GSa/s) and 10-bit respectively cannot meet the requirements of ultra-wide-band applications, because of its inherent electrical bottle-neck such as clock jitter and sampling aperture, etc.^{[1– 5]} All-optical ADC has attracted much attention because it can cope with the problems in electrical field, meanwhile achieve appropriate resolution and sample rate. For instance, Kang et al. realized effective-number-of-bits of 4.22 bit by using cascade optical quantization scheme, ^[6] Satoh et al.^[7] and Konishi et al.^[8] realized the state of art 5- and 6-bit resolutions by soliton self-frequency shift (SSFS) and spectral compression techniques. Kang et al.^[2] realized 6-bit quantization resolution by using a 10m-long high-nonlinear fiber and 10m-long dispersion increasing fiber (DIF).^[2] However, the fiber with a length of more than 100m was used to realize all-optical quantization, which is disadvantageous for photonics integration.

In this paper, we optimize a proposed all-optical ADC by utilizing a 10m-long high-nonlinear photonic crystal fiber (PCF) as a large scale SSFS module and a 10m-long hybrid cladding hexagonal-octagonal PCF (6/8-PCF) instead of 100m-long DIF as a spectral compression module. The simulation results show the frequency shift effect and the spectral compression efficiency, and verify the feasibility of our optimized scheme.

In our proposed all-optical ADC, SSFS and spectral compression as key techniques are utilized to realize all-optical quantization due to temporal power dependence property of frequency shift and further enhance quantization resolution.

The pulse propagation in a high-nonlinear fiber can be described by higher-order nonlinear Schrö dinger equation.^[9] When the optical pulse width is narrower than 5 ps or femtosecond scale, Raman scattering cannot be ignored, which can induce the frequency shifting. The higher-order nonlinear Schrö dinger equation is expressed as follows:

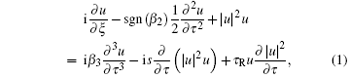
where u is the normalized amplitude envelope; ξ is the normalized transmission distance; τ is the normalized delay time; β ₂, β ₃, s, and τ _R are the second-order and the third-order dispersion parameter, self-steeping, and Raman scattering coefficient, respectively. SSFS^{[10– 16]} is mainly contributed by self-steeping and Raman effects on the right-hand side of Eq.  (1). High frequency of optical pulse will amplify low frequency through Raman scattering effect within optical pulse. With the increase of the transmission distance, the energy transfer shifts toward the red region of the optical spectrum. The frequency shifting is caused by pulse self-steeping and third-order dispersion effects. When ultra-short optical pulse propagates through a fiber, the peak of optical pulse will shift to its back. The group velocity relating to the power of the optical pulse induces an optical pulse self-steeping effect. The third-order dispersion effect cannot be ignored when the central wavelength of optical pulse is near the zero-dispersion wavelength. If β ₃ > 0, the third-order dispersion effect causes the soliton frequency to shift away from the zero-dispersion wavelength, and vice versa, then shift to the zero-dispersion wavelength.

Spectral compression^{[17– 20]} is attributed to self-phase modulation (SPM) term on the right side of Eq.  (1). The SPM effect could broaden and also compress optical spectrum, depending on the chirp of input pulse. Even if the initial chirp is zero, the optical pulse will become chirped pulse in fiber. The spectral compression ratio is limited by fiber dispersion. The high nonlinearity and low dispersion are expected to produce high-efficiency spectral compression of chirped optical pulse. For the hyperbolic secant optical pulse, by solving GNLSE and making simplification, we can obtain two significant parameters as follows:

where T₀ and C are width and chirp of input optical pulse respectively, and s = sgn(β ₂) = ± 1. From Eq.  (2), we can obtain compression ratio F_c

From Eq.  (3), when sC < 0, optical pulse can be compressed (F_c > 1). In other words, it is satisfied that β ₂C < 0 to compress pulse. The positive chirped pulse needs the negative group velocity dispersion (GVD) to realize spectrum compression, while the negative chirped pulse requires the positive GVD to achieve spectrum compression. Pulse compression is a summation process of two opposite components in fiber, so that the variation of T₁ cannot be judged easily.

According to the above theoretical analysis and the proposed optical quantization scheme, we optimize the 6-bit all-optical quantization approach by using high-nonlinear PCF and hybrid cladding 6/8-PCF as the nonlinear transmission medium. The optimized schematic diagram is shown in Fig.  1. Employing the optical parametric process or an optical attenuator, the initial analog signal sampling is first realized. Then, the sampled discrete optical pulses with different values of power are delivered into the first segment of PCF, which has a 1.7-μ m-diameter core with 2% Ge and 80% air, ^[2] to realize all-optical quantization with SSFS effect. Quantized pulses are subsequently fed into the second segment of hybrid cladding 6/8-PCF to achieve the spectrum compression. Finally, an arrayed waveguide grating (AWG) separates the compressed quantized optical signals from each other.

In our optimized simulation scheme, a hyperbolic secant optical source is still utilized with 200-fs full width at half maximum (FWHM), 40-GHz repetition frequency, and 1550-nm central wavelength to compare with the proposed scheme under the same quantization resolution condition. In the SSFS module, the structure of hybrid cladding 6/8-PCF^{[2, 3]} whose air-holes of the first and the second innermost rings around the core are of hexagonal structure and the other rings are of octagonal structure is shown in Fig.  2. By including hexagonal ring lattice structure in the cladding region of the conventional octagonal PCF and adjusting the sizes of air holes around the two innermost cladding structure, the hybrid cladding 6/8-PCF has low flattened dispersion and low confinement loss characteristics than conventional PCF. The hybrid cladding 6/8-PCF has an extra air-hole ring in the innermost ring with hexagonal lattices of relatively small diameters carefully inserted in the original core region on the first two rings compared with conventional PCF. As is well known, the mode field mismatching of the two kinds of PCFs is the main cause of the splicing loss. An intermediate fiber can be used to achieve the mode field matching based on conventional arc discharge welding technology and the total splicing loss can be reduced to < 1  dB.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Schematic diagram of optimizing the proposed optical quantization. SSFS: soliton self-frequency shifting, OPA: optical power attenuator, PCF: photonic crystal fiber, AWG: arrayed waveguide grating.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Structural diagram of the hybrid cladding 6/8-PCF.

Figure  3(a) shows the chromatic dispersion characteristic of the hybrid cladding 6/8-PCF. An ultra-flattened chromatic dispersion of 13.5± 1%  ps/nm· km is obtained in the band from 1430  nm to 1750  nm. In the inset of Fig.  3(a), the mode field distribution is almost circular and confined well within the inner ring. As shown in Fig.  3(b), the effective mode area is 12.3  μ m² and the confinement loss is 5 × 10^{− 5}  dB/km at 1550  nm, respectively. The confinement loss of the second order mode is found to be very small, the hybrid cladding 6/8-PCF can operate effectively as a single mode fiber (SMF) in the telecommunication window.

We record SSFS variation diagrams at several typical input optical power values as shown in Fig.  4(a). With increasing the input optical pulse peak power, the central frequency moves toward the lower frequency region. When the initial peak power is 370  W, the central frequency moves to 162  THz, 31.5-THz frequency shift is obtained in other words. Meanwhile, some high frequency components emerge in the spectrum as shown in the inset (solid line) in Fig.  4(a). With the increase of the initial peak power, the condition of the base-order soliton case (0.5 < N_S < 1.4) cannot hold. The high-order soliton fission takes place in high nonlinear PCF based on the self-steeping, Raman and high-order nonlinear effects, so some high frequency small pulses will emerge. Here, we complement the effects of different input pulse widths and fiber lengths on the frequency shift as shown in Figs.  4(b) and 4(c). All currents of the frequency shift are proportional to the input pulse width and fiber length. With the increase of input pulse peak power, the frequency shift increases. However, it does not mean that the larger frequency shift can be achieved through continually increasing fiber length. From the curve of P₀ = 370  W in Fig.  4(c), the slope of the curve becomes smaller with the increase of fiber length, and in the spectrum there appear some high frequency components after the length of 11  m.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Characteristic curves of hybrid cladding 6/8-PCF. (a) Curve of dispersion versus wavelength, with inset showing the fundamental mode distribution corresponding to 1550  nm. (b) Curves of effective mode area and confinement loss versus wavelength.

In order to enhance quantization resolution N that is expressed as follows:

where λ _shift is the wavelength shift in SSFS module and Δ λ _FWHM is spectral FWHM, a smaller Δ λ _FWHM should be obtained in spectral compression module based on achieving 31.5-THz frequency shift previously. In a spectral compression module a 10m-long hybrid cladding 6/8-PCF is utilized as a spectral compression medium instead of 100m-long DIF, meanwhile, we obtain the same quantization resolution.

The spectra of non-chirp optical pulse after the spectral compression module are recorded with different input peak powers of the module as shown in Fig.  5(a). The widths of output spectrum monotonically decrease with the increase of the peak power. Because optical pulse will become chirped pulse when it propagates in fiber, even if C = 0. When the peak power is 3  W, a 7-nm FWHM is obtained. The spectral compression ratio is 1.71. If we continue to increase the input peak power, the spectral width does not become narrower. Conversely, the oscillation of spectrum base is intensified. In

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Spectrum complementary analyses after SSFS module. (a) Variations of normalized intensity with frequency for different input peak powers. (b) Curves of frequency shift versus input pulse width for different input peak powers. (c) Curves of frequency shift versus fiber length for differen input peak powers.

order to reduce the output spectrum width and further enhance quantization resolution, a pre-chirp process is utilized before spectral compression module. The pre-chirp process is easily obtained through a small segment of fiber. The spectrum diagram with + 1 initial chirp is shown in Fig.  5(b). Obviously, the output spectral width is narrow compared with that in Fig.  5(a). When the peak power is 5.5  W, the spectrum compression ratio is 6.28. According to the previous simulation results, 6-bit quantization resolution is still obtained even through 100m DIF is replaced, meanwhile, the fiber length is shortened to 1/10 of the original. The plots of pre-chirp versus compression ratio for different input peak powers are shown in Fig.  5(c). The compression ratio first rises and then decreases in each case of input power, with the increase of pre-chirp. There appears a maximum compression ratio in any curve. Meanwhile, the compression ratio is improved with the increase of input peak power.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. Spectrum analyses after spectral compression module. Variations of normalized spectrum power with wavelength when (a) C = 0 and (b) C = + 1 for different input peak powers. (c) Curves of compression ratio versus pre-chirp for different input peak powers.

When input peak power of spectral compression module maintains 5.5  W, the spectra of non-chirp and + 1 initial chirp optical signal are recorded with different lengths of 6/8-PCF as shown in Figs.  6(a) and 6(b), respectively. The spectral width does not become narrow obviously with the increase of 6/8-PCF length compared with ones of 10m-long fiber. Because the effective fiber length exists to obtain maximum spectrum compression ratio^[10] as shown in Fig.  6(c). The maximum compression ratio is a fixed value at a fixed fiber length and determined by the input initial chirp. Spectrum of pre-chirp pulse will be compressed (1 + C²)^{− 1} times compared with one of non-chirp, so compression ratio has a maximum value.

Fig.  6.

	Figure Option ViewDownloadNew Window
	Fig.  6. (a) Variations of normalized spectrum power with wavelength with C = 0 (a), and C = + 1 (b), for different fiber lengths. (c) Variations of compression ratio with pre-chirp different fiber lengths.

In this work, we optimize a proposed optical quantization scheme for all-optical ADC by utilizing SSFS and spectral compression module based on PCF. On the premise of ensuring 6-bit quantization, a 10m-long hybrid cladding 6/8-PCF is utilized as a spectral compression medium instead of a 100m-long DIF. The effective compression is obtained when + 1 pre-chirp is added. By comparison with previous proposed approach, the total fiber length of the whole system is only 20  m so that the optimized scheme is a good approach in the sense of integration and miniaturization. Therefore, our optimized quantization approach for all-optical ADC can cater for implementing ultra-wide-band applications.