†Corresponding author. E-mail: zhaoyingwang@zju.edu.cn
‡Corresponding author. E-mail: qlin@zju.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 11174249 and 61475139), the National High-Technology Research and Development Program of China (Grant No. 2011AA060504), and the National Key Basic Research Program of China (Grant No. 2013CB329501).
Rb atom motion in a magneto–optical trap (MOT) consisting of a partially spatially coherent laser (PSCL) is investigated theoretically. The spatial coherence of the laser is controlled by the electro–optic crystal. The instantaneous spatial distribution of the dissipative force induced by the PSCL on an Rb atom is varying with time stochastically. The simulated results indicate that compared with a fully coherent laser, the spatial coherent laser has effects on the atomic trajectories; however, the capture velocity and the escape velocity are kept the same. The main reason is that the spatial coherence of the laser fluctuates temporally and spatially, but the average photon scattering rate varies little, which makes the total number of atoms and the atomic density distribution unchanged.
Because of the ability to slow, focus, and trap atoms, laser cooling is attracting more and more attention in practical applications, including atom lithography, [1] atom clocks, [2– 4] atom interferometer, [5– 7] precision measurements of fundamental constants, [8, 9] and atom optics.[10, 11] With the study going on, various ideas and experimental technologies for atom cooling are proposed and developed.[12, 13] These can make the temperature of an atomic cloud decrease to nanokelvin, meanwhile the coherence of an atom wave will be enhanced. So the reflection, focusing, interference, and diffraction of an atom beam can be realized.[14]
The basic principle of laser cooling is the momentum exchange between the atoms and the laser light, and the light should be at or near the resonance frequency of atomic transition.[14] In order to accomplish this process, there are some techniques, such as laser frequency sweeping, varying the atomic resonant frequency with a magnetic or electric field, varying the Doppler shift by diffuse light and broadband light. These techniques all focus on the temporal coherence of laser. However, due to the effect of randomness of the spontaneous emission inside the laser, all the amplitudes of electric field, frequency, and phase will be irregular-fluctuated.[15, 16] So the coherence will be disturbed by these fluctuations. So it is interesting to explore the interaction between the partially coherent laser and the atoms.[17] However, up to now, all studies about laser cooling have focused on the temporal coherence since the first achievement of laser cooling. Yet, the influence of the spatial coherence of the cooling laser on the atoms has been investigated little.
In this paper, the characteristics of dissipative force deduced from the spatially partially coherent laser, the capture, and escape of Rb atoms in the MOT are investigated theoretically. A semiclassical numerical model is established to simulate the atomic behavior in the MOT. In the simulations, an atom is represented as a two-level system, and the induced dipole electric forces and collision losses are ignored. The atom is considered as a point particle whose motion is described by Newton’ s laws. The simplified model results from the fact that the temperature in the MOT is not low enough to highlight the effects of an atomic de Broglie wave.[14] This model allows the calculation of the atomic trajectories and the understanding of the detailed dynamics of the atom cooled by PSCL.
In Ref. [17] the authors proposed a scheme to achieve the partially spatially coherent laser (PSCL) with the electro– optic phase modulation of LiNbO3 (LN) crystal. When a high ac voltage is applied to the crystal along the laser axis, the refractive index of the crystal will be changed. Thereafter, the laser beam can acquire an additional phase φ (written by Eq. (1)) that is proportional to the external electric field intensity. This dependents on both the spatial position and time, which are written by Eqs. (2) and Eq. (3), respectively.[17, 18]

where l is the length of the LN crystal, γ 22 and n0 are the electro– optic coefficient and refractive index of the LN crystal, respectively, and λ is the wavelength of the laser beam.

where t is the time.

where C is the cross-section electric capacity between the electrodes, U is instantaneous electric potential on the two electrodes, 2a is the distance between the two electrodes, b is the width of the electrode, and ε is the dielectric constant of the crystal.
The dissipative force is written as[14]

where Γ is the nature linewidth of a Rb atom, k is the wave vector, and ħ is the Planck constant divided by 2π . Here the saturation parameter s is given by

where I(r) is the laser intensity, r is the position vector, Is is the atom saturation intensity, and Δ is the effective detuning given by
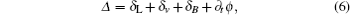
where δ L is the laser frequency detuning, δ v is the Doppler shift due to the atomic motion, δ B is the magnetic Zeeman shift, and ∂ tϕ is variable shift by the random phase.
For the magneto– optical trap, the total scattering force on the atoms is the sum of the six laser beams, and can be written as

With Eq. (7), we can calculate the scattering forces on the Rb atom under different physical conditions. Some calculated parameters are shown in Table 1. The unit 1 Gs = 10− 4 T.
| Table 1. Some calculated parameters. |
Considering the equivalence of the three mutually orthogonal counter-propagating laser beams, we only do the simulations in the x direction. In addition, here we use “ with modulation” and “ without modulation” to describe the “ PSCL” and “ coherent laser” , respectively.
Figures 1(a) and 1(b) show the instantaneous spatial distributions of the dissipative force within the plane of x = 0, with modulation and without modulation, respectively. The laser axis is perpendicular to the paper surface at the point (y, z) = (0, 0). Figure 1(c) shows the profiles of the force in the y direction, varying with interaction time. The curves in the direction of the arrow, from upper to lower are for different conditions: without modulation, and with modulations for instantaneous times of 5, 100, 0, 25, and 50 μ s, respectively. In these figures, the forces are in units of ħ kΓ , equal to 3.2306 × 10− 20 N for the 87Rb transition 52S1/2, F = 2 → 52P3/2, F′ = 3; the parameter x = 0; the atomic velocity is 1 m/s in all the three directions.
Figures 1(a) and 1(b) show clearly the differences in force distribution between the laser with modulation and the laser without modulation. It can be seen that close to the laser axis, in the case with modulation, (Fig. 1(a)), the distribution of the force features concentric circles, the same as the distribution of the force in the case without modulation shown in Fig. 1(b), but it has a higher force gradient. Moreover, off the laser axis, the concentric circles will be disturbed due to the modulation. The distributions between the y direction and the z direction are different, which are the directions parallel and perpendicular to the direction of the connection line between electrodes located on the LN crystal, respectively. From Fig. 1(c), we can see that for a fixed position, the force with modulation is varying with time stochastically; the absolute value with modulation is larger than that without modulation. This results from the ac modulation of LN.
According to the dissipative force, we can compute the equation of motion for each atom to obtain atomic trajectories under different conditions. The motion equation is written as

where j means one coordinate axis, x or y or z; d Pj is the atom momentum, and d Pj· recoil is the atom momentum due to the random nature of the absorption and spontaneous emission of the photons.
The motion equation (8) is integrated by employing an adaptive step size, fourth-order Runge– Kutta type algorithm by Matlab. The initial positions and velocities of each atom are chosen as shown in the following figures. The integrating time is set to be 50 ms. The curves of simulated atomic trajectories can show the variations of the velocity and position of a Rb atom in the MOT. Here we will focus on the capture and escape process of the atoms.
Figures 2(a) and 2(b) show the trajectories of atoms in the escape process under lasers with modulation and without modulation, respectively. For the curves in the direction of the arrow, from lower to upper, the initial velocities in the x direction are 18, 18.25, 18.5, 18.75, 19, and 19.25 m/s. The initial position of each atom is assumed to be in the trap’ s center and the velocities in y and z directions are both zero.
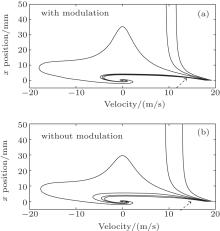 | Fig. 2. Trajectories of the atoms in the escape process in the cases (a) with and (b) without modulation. |
From Fig. 2, it can be seen that the atom trajectories trapped in the lasers with modulation are similar to those without modulation. The atoms with the initial velocity smaller than 18.75 m/s can be trapped to the center again. Figure 3 shows the detailed differences between trajectories of atoms with a velocity of 18.5 m/s. It indicates that the atom trajectory in the MOT with modulation is closer to the trap’ s center than that without modulation.
The phenomenon in Fig. 3 confirms the results in Ref. [14]. The escape velocity mainly depends on the collision between the cold atoms and the hot atoms. So it feels the unnoticeable effect of the modulation term ∂ tϕ . However, due to the phase modulation, the absolute value of instantaneous scattering force with modulation is bigger than that without modulation. So the atomic trajectory will twist more to the trap center for the beam with modulation.
 | Fig. 3. Trajectories of atoms with a velocity of 18.5 m/s in the escape process for the cases with and without modulation. |
Figure 4 shows the trajectories of the atoms in the capture process. For curves in the direction of the arrow, from lower to upper, the initial velocities in the x direction are 3, 3.25, 3.5, 3.75, and 4 m/s. The initial position of each atom is assumed to be at the trap’ s edge and the velocities in the y and z directions are both zero.
 | Fig. 4. Trajectories of the atoms in the capture process for the cases (a) with and (b) without modulation. |
From Fig. 4, it can be seen that the trajectories of the atoms in the MOT with modulation are similar to those without modulation. The atoms with the initial velocity smaller than 3.75 m/s will be trapped to the center again. Figure 5 shows the detailed differences in atom trajectory of an atom with a velocity of 3.5 m/s between the cases with and without modulation. It indicates that the trajectories of the atoms in the MOT with and without modulation are very close to each other. When moving, they can crossover or even overlap each other.
 | Fig. 5. Trajectories of an atom with a velocity of 3.5 m/s in the capture process in the cases with and without modulation. |
The phenomenon in Fig. 5 confirms the results in Ref. [17]. The capture velocity depends on the photon scattering rate, which is proportional to the scattering force, and dependent on the term ∂ tϕ . Because the average scattering rate does not vary with the phase modulation, the capture velocity has an unnoticeable change for the PSCL. Like the escape velocity, due to the phase modulation, the absolute value of instantaneous scattering force is larger than that without modulation. So the atom will be subjected to a larger force with modulation. Then its trajectory will twist more to the trap center.
The above simulations indicate that due to the modulation with the electro– optic crystal, the instantaneous spatial distribution of dissipative force induced by the PSCL on a Rb atom is varying with time stochastically. Although the PSCL can disturb the atomic trajectory in the MOT, it can still cool and trap the atoms in the MOT. Moreover, the capture velocity and the escape velocity remain the same for the fully spatially coherent and PSCL. As is well known, the capture velocity determines the number of MOT atoms, so it can be directly concluded that the spatial coherence of a laser has little influence on the total number of atoms, and the long enough loading time can ensure a constant number of atoms. In addition, the average photon scattering rate does not vary with the spatial coherence of the laser, and the atomic density is mainly limited by the photon scattering, so, the atomic density distribution changes little for the partially spatially coherent laser cooling. Further work will be done to produce a steady velocity distribution of the atoms and deduce the equilibrium temperature by calculating the root-mean-square velocity of the atoms.
| 1 |
|
| 2 | [Cited within:1] |
| 3 |
|
| 4 |
|
| 5 | [Cited within:1] |
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|



