As is well known, the behavior of atom or ion in an external field or surface is quite different from that in free space.^{[1– 5]} For instance a photodetachment cross section of an ion or molecule shows an oscillatory structure in the presence of a field and or wall in contrast to their smooth behavior in free space. Blumberg et al. in early 1979, observed oscillation behavior in the photodetachment cross section of a negative ion in a magnetic field.^[1] Bryant in 1987 observed a ripple-like structure in the photodetachment of H⁻ placed in an electric field.^[2] Later on, Rau and Wong pointed out that such a ripple structure resulted from the interference between the detached-electron waves going up and down the electric potential barrier.^[3] In many such cases, a semi-classical treatment has been found to be more fruitful than a quantum-mechanical treatment and the characteristics of the quantum spectra can be directly related to the family of classical orbits. A significant success in this regard was achieved by Du and Delos^[4] and Gao and Delos^[5] in developing a semi-classical theory called “ closed orbit theory” and successfully explaining the oscillation in the complicated spectrum for an atom or negative ion in an external field. They attributed oscillation in the cross section to the interference of the detached-electron wave reflected by the field and source of localized wave in the vicinity of the bound state of the atom or ion. Now closed orbit theory is also conveniently being used to study the photodetachment of a negative ion near surface. Another useful mathematical tool to investigate the problems of the photodetachment process of a negative ion near surface is the theoretical imaging method.^[6]

The interaction of an atom and/or ion with a surface has practical interest in various physical, biological, and chemical processes.^[7] The presence of a surface changes the dynamical property of the atom or ion.^[8] For instance, the presence of a surface modifies the photodetachment cross section and the resonance life time of an adsorbed ion due to a change in the barrier penetrability of the photodetached electron.^{[9, 10]} Recently, with the development of surface physics, the photodetachment process of a negative ion near a surface has been studied extensively so as to understand the interesting properties of the negative ion and surface. Since H⁻ has been considered to be used to investigate adsorbate state lifetime and charge transfer during backscattering, ^[11] the photodetachment of H⁻ near an interface has received much attention. In 2006, Yang et al.^[12] investigated the photodetachment cross section of H⁻ near an elastic wall with linear polarized laser light travelling along the z direction (z-polarized light) by closed orbit theory. They successfully explained the wall-induced oscillations in the total cross section. At about the same time, ^[13] they investigated photodetachment of H⁻ near an elastic wall in a static electric field both by closed orbit theory and by the quantum mechanics approach. Subsequently, Yang et al.^[14] investigated photodetachment of H⁻ near an inelastic surface by defining a reflection coefficient α such that α < 1. Afaq and Iftikhar^[15] have revisited the photodetachment of H⁻ near inelastic surfaces by using the closed orbit theory through introducing a new parameter called the reflection parameter to account for the inelastic behavior of the surfaces. Recently, a photodetachment cross section of H⁻ near a hard spherical surface has also been investigated by the theoretical imaging method.^{[16, 17]}

In the previous studies, the photodetachment cross section of H⁻ near interfaces has been investigated by focusing only on z-polarized laser light. Du^[18] firstly studied photodetachment of H⁻ in a static electric field with an arbitrary laser polarization direction. As to the photodetachment process of H⁻ near a hard wall with laser light travelling in an arbitrary polarization direction, no work has been reported. In this article we derive an analytical expression for the photodetachment cross section of H⁻ near a hard wall for an arbitrary laser polarization direction by the closed orbit theory.

We hope the results of this simple elastic wall model will be helpful in exploring the photodetachment processes of ions near interfaces, cavities, and ions traps. Throughout the article, the atomic units (a.u.) are used unless otherwise mentioned.

The closed orbit theory in our problem can be explained as follows: a photon is absorbed by the hydrogen negative ion and the electron is detached according to the laws of quantum mechanics. The detached-electron wave moves in all possible directions. Close to the nucleus (≤ 50  a.u., the unit a.u. is the atomic unit), the electron goes into a near-zero-energy outgoing wave where the external effects are negligible. Far from the nucleus (≥ 50  a.u.), the outgoing wave propagates according to the semiclassical mechanics and correlates with outgoing classical trajectories. Eventually, this classical wave is reflected by the hard wall and turns back to the vicinity of the nucleus. The interference between the returning, i.e., incoming classical wave and steadily produced outgoing wave leads to oscillations in the total photodetachment spectrum. Thus, closed orbit theory beautifully connects the phenomenon of quantum interference to classical orbits followed by the detached electron wave.

The rest of the paper is organized as follows. In Section  2, we describe the classical motion of the detached-electron from H⁻ near a hard wall and then obtain the analytical expression of total photodetachment cross section of this system based on closed orbit theory. In Section  3, we present key numerical results and the relevant discussion involving the physical explanation of oscillations in cross section. In Section  4, we give some conclusions of our work.

To analyze the photodetachment process of H⁻ near a hard wall, we place a hydrogen negative ion H⁻ at the origin and apply a beam of laser travelling in arbitrary polarization direction (θ _L, φ _L) to detach an electron from H⁻ . A hard wall is placed perpendicularly to the z axis at a distance d from the source as shown in the schematic diagram in Fig.  1.

After the photodetachment process, the loosely bound electron detaches and moves away from the source. The photo-detached electron wave function ψ _d satisfies the inhomogeneous Schrö dinger equation with source term given by^[19]

Here, E is the kinetic energy of the detached-electron, which is equal to the photon energy minus the binding energy of the hydrogen negative ion: E = E_ph− E_b. The Hamiltonian, H = p² / 2+ V_p(r), governs the motion of the detached-electron and ψ _i is the initial wave function of the bound state of H⁻ in configuration space, defined as Be^{− k_b} / r, where B is a normalization constant with a value of 0.31552, and k_b is the momentum with a magnitude of 0.2355882 and related to the binding energy of the bound state of H⁻ , which is approximately taken to be 0.754  eV. The dipole operator D is z or 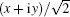, for linear or circular polarized laser photons, respectively.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Schematic diagram for photo-detachment of H− near a hard wall. The solid vertical line from the source to the wall represents a closed orbit. The trajectories of the detached electron emanating from the source are shown by the curved lines and they never turn back to the nucleus after reflection from the wall.

Initially, H⁻ is in S state; right after detachment near the nucleus the detached-electron produces a P wave by carrying one angular momentum due to selection rules. As the detached electron is out of the influence of the atomic core potential while being far from it, we can neglect the short-range potential V_p(r).

In order to solve Eq.  (1) near the nucleus, the photo-detached wave function ψ _d is decomposed into direct and returning parts: ψ _d(r) = (ψ _d)_dir(r) + (ψ _d)_ret(r) as done in Ref.  [19]. The direct part represents the steady outgoing detached-electron wave initially going out from the atomic core after photodetachment and never leaves the core. The returning part represents the outgoing detached-electron wave that propagates semiclassically far from the nucleus along the negative z axis and then turns back to the nucleus after being reflected from the hard wall, thus following a closed orbit. The interference between the returning wave and the steady outgoing wave in the vicinity of an atomic core produces oscillation in the photodetachment cross section. The wave function (ψ _d)_ret(r) is physically the continuation of (ψ _d)_dir(r) along the closed orbit.

The direct part of the outgoing detached electron wave satisfying Eq.  (1) in terms of outgoing spherical Hankel function ^[20] is given by

where the factor

describes the dependence of detached-electron wave function on the outgoing direction (θ , φ ).

In the absence of a hard wall, the smooth background oscillator strength density is given by the overlap integral of the direct part with the source

Using Eq.  (2) and ψ _i = Be^{− k_b}/r in Eq.  (4) and then evaluating the integral we obtain

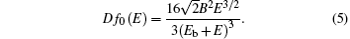
Now the background photodetachment cross section from the oscillator strength density is calculated as

or

To obtain the semi-classical approximation of the returning wave function along the closed orbit, we consider a sphere centered at the origin, with radius R = 10a₀ (a₀ is the Bohr’ s radius in atomic units). We take the size of the sphere to be large enough so that the asymptotic approximation of Hankel function 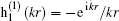is fairly valid at its surface, while the Coulomb interaction of the core is weak enough outside the sphere and can be neglected. The sphere is also small enough so that electron motion is not affected by the hard wall. The direct outgoing wave on the surface of the sphere is given by

When the outgoing wave moves out from the sphere, both its amplitude and phase are changed. After reflection from the wall, the semiclassical wave returns to the nucleus as a plane wave travelling in the z direction. Therefore,

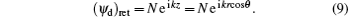
The resulting expression of N is a product of initial outgoing wave travelling along the negative z direction, amplitude A and a phase factor, i.e.,

Substituting Eq.  (8) into Eq.  (10) yields

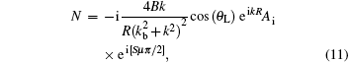
where S is the action integral ∫ pdq along the closed orbit from the surface back to the source, A is the amplitude for the detached electron wave, and μ is the Maslove index representing the geometrical features of the trajectory and its neighboring trajectories which is 1 in our case. Consequently, the new expression for N with the limit of small R will become

where the value of action integral , while the amplitude A along a closed orbit along the z axis is given by

Using the values of S and A in Eq.  (12) we obtain

Therefore, the returning semi-classical wave in Eq.  (9) becomes

Therefore, oscillator strength density in the presence of a hard wall is given by the overlap integral of the returning wave with the source term as

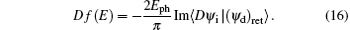
After evaluating the overlap integral, we obtain

The corresponding oscillatory photodetachment cross section is given by

or

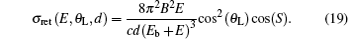
Now combining Eqs.  (7) and (19) we obtain the total photodetachment cross section

where c = 137.037. Therefore, the total photodetachment cross section of H⁻ for an arbitrary laser polarization direction near a hard wall is the sum of the smooth background term and the oscillatory term as given in Eq.  (20). The cross section evidently depends on laser polarizing angle θ _L, inter-source wall distance d, and photon energy, . The first smooth background term on the right-hand side of Eq.  (20) is the total detached outgoing electron flux in the absence of a hard wall. It is the same as what was obtained for the z-polarized laser light in Ref.  [12], but the oscillatory term acquires an additional angular factor cos²(θ _L). However, the phase of oscillations here remains the same as that in the z-polarized case. The oscillatory term is due to the quantum interference between the steady outgoing detached-electron wave and the classical returning electron wave. The phase accumulation factor S determines the sign of interference, and the angular factor cos²(θ _L) determines the influence of laser polarization direction on the oscillations in the cross section. The hotodetachment cross section for H⁻ obtained in Ref.  [12] given in Eq.  (19) is a special case of our formula at θ _L = 0.

In a more compact form, the total cross section in Eq.  (20) can be written as

where

is the smooth background term, and is the action integral.

Our analytical formula for the total photodetachment cross section of H⁻ near a hard wall given in Eqs.  (20) and (21) is similar to that in Ref.  [18] for the static electric field given in Eqs.  (14) and (15). The extra angular factor cos²(θ _L) evidently controls oscillation in total cross section. In a static electric field, the cross section at the threshold is non-zero (Fig.  1, Ref.  [18]) due to interference of the field potential with the core atom arising from the phenomenon of tunneling. However, in our case the total cross section at the threshold is zero because the wall has no effect on the core electron. The dependences of the photodetachment cross section given in Eq.  ( 20) on the laser polarization direction and inter-wall source distance are shown in Figs.  2 and 3, respectively. As shown in Fig.  2, the laser polarization direction θ _L with respect to the z axis has a considerable influence on the oscillation in total cross section. At θ _L = 0, i.e., when the laser polarization direction is perpendicular to the wall, the amplitude of oscillation in the cross section is maximum as represented by the dashed oscillatory thick curve in Fig.  2. It must be the case because in this situation photodetached-electron waves emanating from the antinode of the outgoing P wave in the direction of the negative z axis are reflected from the wall and return to the nucleus, thus forming a closed orbit which in turn contributes to oscillation in total cross section. While at θ _L = π /2, i.e., when the laser polarization direction is parallel to the hard wall, no more oscillation is seen in the total cross section as represented by the solid smooth curve in Fig.  2. It is because in this situation almost no photodetached-electron wave emanating from the antinode is reflected back to the source from the wall. Moreover, photodetached-elctron waves emitted from the node of the P wave are almost negligible. As a result, there is no detached-electron wave to be reflected back to the source and the formation of a closed orbit is not possible and we have no oscillation in the cross section. While at polarizing angle θ _L = π /4, the amplitude of oscillation is half of the maximum and minimum values at θ _L = 0, and θ _L = π /2, respectively. These results are very much consistent with our theoretical formula derived in Eq.  (20).

Fig.  2.

Figure Option ViewDownloadNew Window

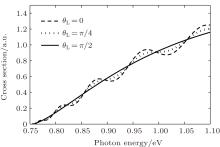Fig.  2. Dependences of photodetachment cross section given in Eq.  (20) on laser polarization direction θ L for a fixed source– wall distance d = 200  a.u. The amplitude of oscillation is maximum when the laser polarization direction is along the z axis, i.e., perpendicular to the wall at θ L = 0 as represented by the dashed oscillatory curve. Oscillation in cross section vanishes at θ L = π /2 when the laser polarization direction is parallel to the wall as represented by the smooth thick curve. At θ L = π /4, the amplitude of oscillation is half of the maximum and minimum values at θ L = 0, and θ L = π /2 respectively.

In Fig.  3, we show how the oscillation amplitude in the total cross section given in Eq.  (20) depends on the source– wall distance at a fixed laser polarization direction θ _L = 0 for a particular range of photon energy. When the hard wall is placed very close to a hydrogen negative ion at distance, d = 50  a.u, the amplitude of oscillation in cross section is maximum. When the wall is placed at a very large distance from the source, d = 5000  a.u., the situation becomes identical to the free space case and no more oscillation is seen in the cross section. Thus the amplitude of oscillation in total cross section decreases by increasing the distance of the wall from the source and vice versa.

Fig.  3.

Figure Option ViewDownloadNew Window

Fig.  3. Dependences of photodetachment cross section on the distance of the wall from the source for a fixed laser polarization direction θ L = 0, i.e., when laser travels along the z direction and is perpendicular to the wall. The amplitude of oscillation in total cross section varies with the wall– source distance. At wall– source distance d = 50  a.u., the amplitude of oscillation is maximum as represented by a dashed oscillatory curve. At large wall– source distance d = 5000  a.u., no more oscillation is seen in the cross section and we recover the free space case as represented by the smooth thick curve.

In this study, we derive a more general analytical expression for photodetachment of H⁻ near a hard wall with arbitrary laser polarization direction by using the closed orbit theory. It is found that the laser polarization direction θ _L considerably controls wall-induced oscillation in the cross section. However, it should be noted that the laser polarization direction influences only the oscillatory term in the total cross section while the smooth back ground term remains the same as what was obtained in the case of z-polarized laser light.^[12] The variation in amplitude of oscillation with laser polarization angle θ _L is explained with the shape of the detached-electron P wave. It is observed that different orientations of node and antinode of the detached-electron P wave depending on the laser polarization direction play an important role in forming single closed orbit which in turn controls oscillation in the cross section. At θ _L = 0, our general formula as given in Eq.  (20) evidently approaches to the one obtained for the z-polarized case given in Eq.  (19) of Ref.  [12]. We hope the results of our simple elastic model will be helpful in exploring the photodetachment processes and photodetachment microscopy of ions near interfaces, cavities, ions traps, and fields. The results may be conducible to understanding surfaces dynamics, e.g., surface potential, band structure of the surface, and properties (e.g. binding energy) of Rydberg atoms, molecule, and ions.