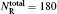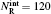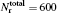Cite this Article
Zhang Jing, Gao Shou-Bao, Wu Hui, Meng Qing-Tian†. State-to-state quantum dynamics of the N(4S) + H2(X1Σ+) → NH(X3Σ−) + H(2S) reaction and its reaction mechanism analysis . Chinese Physics B, 24(8): 083104  
Permissions
State-to-state quantum dynamics of the N(4S) + H2(X1Σ+) → NH(X3Σ−) + H(2S) reaction and its reaction mechanism analysis
Zhang Jinga), Gao Shou-Baoa), Wu Huib), Meng Qing-Tian†a)
College of Physics and Electronics, Shandong Normal University, Jinan 250014, China
State Key Laboratory of Molecular Reaction Dynamics, Dalian Institute of Chemical Physics, Chinese Academy of Sciences, Dlian 116023, China

†Corresponding author. E-mail: qtmeng@sdnu.ed.cn

*Project supported by the National Natural Science Foundation of China (Grant No. 11074151) and the Natural Science Foundation of Shandong Province, China (Grant No. ZR2014AM022).

Abstract

Quantum state-to-state dynamics of the N(4S) + H2 (X1Σ+) → NH(X3Σ−) + H(2S) reaction is reported in an accurate novel potential energy surface constructed by Zhai et al. (2011 J. Chem. Phys.135 104314). The time-dependent wave packet method, which is implemented on graphics processing units, is used to calculate the differential cross sections. The influences of the collision energy on the product state-resolved integral cross sections and total differential cross sections are calculated and discussed. It is found that the products NH are predominated by the backward scattering due to the small impact parameter collisions, with only minor components being forward and sideways scattered, and have an inverted rotational distribution and no inversion in vibrational distributions; both rebound and stripping mechanisms exist in the case of high collision energies.

PACS: 31.15.xv; 34.50.–s; 03.67.Lx
Keyword: state-to-state quantum dynamics; time-dependent wave packet; differential cross section; N(4S) + H2
1. Introduction

The reactions involving nitrogen atoms play an important role in atmospheric chemistry and many combustion and explosion processes.[1– 3] Thus, nitrogen atom reactions, particularly with hydrogen, have received considerable attention.[4– 12] In this paper, we focus on the simplest nitrogen triatomic reaction, i.e., the N(4S) + H2 (X1Σ + ) → NH(X3Σ − ) + H(2S), an important reaction in thermal decomposition of cyclotrimethylenetrinitramine (C3H6N6O6) and cyclotetramethy-lenetetranitramine (C4H8N8O8), which are nonnegligible ingredients in solid propellants used for rockets and guns.[2]

Early experimental measurement by Koshi et al. established the rate constant of the N(4S) + H2 (X1Σ + ) → NH(X3Σ − ) + H(2S) reaction in a high temperature range of 1600  K– 2300  K. An Arrhenius expression was observed, i.e., K(T) = (2.8 ± 0.2) × 1014exp(− 33 ± 7(kcal/mol)/RT)  cm3· mol− 1· s− 1.[4] In order to obtain the mechanism of this reaction, Koshi et al. also carried out the quantum-mechanical calculations. The obtained forward and reverse barriers for quartet state reaction are 35.3  kcal/mol and 4.4  kcal/mol, respectively, which are in good agreement with the experimental results.

At the forefront of the theoretical studies, with the purpose of understanding the mechanisms of the N(4S) + H2 (X1Σ + ) reaction, several groups have paid much attention to constructing the potential energy surface (PES).[7– 9, 12] The first PES for the N(4S) + H2(X1Σ + ) reaction was constructed by Takayanagi et al.[7] based on high-level second-order multiconfigurational quasi-degenerate perturbation method (MCQDPT2)//6-311 + G* * calculations, with the multi-reference configuration interaction (MRCI) method. Subsequently, Pascual et al.[8] constructed the PES of the NH2 reactive system and calculated the rate constants of the N(4S) + H2(X1Σ + ) reaction and its reverse reaction by employing the quasi-classical trajectory (QCT) method and variational transition state theory (TST). The results were found to be in good agreement with the available experimental[4, 5] and theoretical data.[7] Poveda and Varandas[9] also reported an accurate PES for the ground state of the N(4S) + H2(X1Σ + ) reactive system, based on the double many-body expansion (DMBE) theory at the MRCI/aug-cc-pVQZ level. The characteristics of the PES revealed that this reaction takes place via an abstraction mechanism rather than the insertion one. Very recently, Zhai and Han[12] constructed a novel global PES for the lowest quartet electronic state 4A″ by using the many-body expansion theory and neural network (NN) method, in which all the ab initio calculations were done using the MOLPRO package and 8645 MRCI points based on the larger aug-cc-pV5Z basis set. The obtained barrier height is lower than the previous theoretical estimates, [6, 7, 9] which can enhance the reaction probability, especially at the lower collision energy. Moreover, the zero-potential energy is closer to the experimental value.[13, 14]

The quantum dynamic studies of the title reaction and the isotopic variants of this reaction have been considered in the previous work.[6– 8, 10– 12, 15] However, there are few relevant calculations of the N(4S) + H2(X1Σ + ) → NH(X3Σ − ) + H(2S) reaction at the state-to-state level. Based on the QCT method, Yu Y Y and Yu Y J, [10] and Zhang et al.[11] calculated the polarization-dependent differential cross sections (PDDCSs) and the three angular distributions of P(θ r), P(ϕ r), P(θ r, ϕ r). Zhang and Dong[15] also performed a QCT study for the N(4S) + H2(X1Σ + ) reaction, including the normal DCSs, P(θ r), P(ϕ r). The results revealed that for the ground vibrational state, the reaction was dominated by the backward scattering process. Even so, there are no relevant time-dependent quantum dynamic calculations to investigate the reaction mechanism of the abstraction reaction N(4S) + H2(X1Σ + ). As is well known, the zero-point energy and the tunneling effect are not taken into consideration in the QCT method, so this calculation method may produce inaccurate results, especially nearby the threshold energy. In order to obtain more detailed and accurate information and an accurate physical understanding of the reaction dynamics, here we employ the time-dependent quantum wave packet (TDQWP) method to calculate the state-to-state quantum scattering dynamics on the new PES of Zhai and Han[12] in a collision energy range of 1.0  eV– 2.0  eV.[16, 17] The remainder of this article is organized as follows. In Section 2, the theoretical methodology is outlined. In Section 3 the results and discussion are presented, and the conclusions are given in Section 4.

2. Theory and methods
2.1. PES

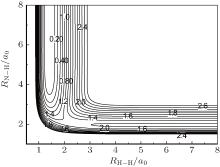
As indicated in Ref.  [12], the novel global PES has been constructed by using many-body expansion with the NN method for the three-body term.[12, 16, 18– 20] The major feature of this present PES is the N– H– H collinear transition state for the N(4S) + H2(X1Σ + ) → NH(X3Σ − ) + H(2S) reaction, which is shown in Fig.  1. It can be clearly seen that at about (2.1a0, 2.4a0) there is a saddle point with a potential barrier height of about 1.25  eV (28.8  kcal/mol), and no well at the collinear configuration of the NH2 reactive system. The adequacy of this new PES for kinetic and dynamic studies has been demonstrated in Ref.  [12].

Fig.  1. Contour plot of the PES for the N– H– H angle of 180° in internal coordinates (energies here are given in eV).

2.2. TDQWP method

The state-to-state quantum reaction dynamic study can provide the most detailed information and offer profound insight into the chemical reaction process. With the development of the modern computer technology, the atom– diatom reactive scattering problems have been mostly solved, including the simple direct reactions such as H + D2, [21, 22] H + HD, [23] F + H2, [24] and the challenging reactions with deep wells such as O + H2, [25] or with multiple potential energy surfaces such as Cl + H2.[26] Here, we report the converged state-to-state differential and integral cross sections for the title reaction, in a collision energy range of 1.0  eV– 2.0  eV. These calculations are carried out with the TDQWP method. While the calculations of differential cross sections (DCSs) have been reported for many triatomic reactions and two tetra-atomic systems up to now, [27] theoretical calculations are still a great challenge to computational time consumption.[28– 34] In this paper, the TDQWP method is efficiently implemented on graphics processing units (GPUs). This new efficient GPU version of the TDQWP code is developed by Zhang and Han and has been proved to be more efficient than central processing units (CPUs) with the test calculations of H + HD and O + HD reactions.[17, 35]

The Hamiltonian of the N(4S) + H2 reaction in body-fixed (BF) reactant Jacobi coordinates can be written as[36]

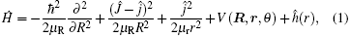
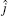
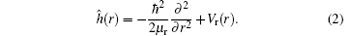
where R and r are, respectively, the atom– diatom and diatomic distances, μ R is the reduced mass between atom N and diatom H2, μ r is the reduced mass of H2, Ĵ is the total angular momentum operator, is the rotational angular momentum operator of H2, V(R, r, θ ) is the interaction potential excluding the diatomic reference potential for the 14A″ state of the NH2 system, and ĥ (r) is the reference Hamiltonian of H2, defined as

The initial wave function of the reactant is prepared in a space-fixed (SF) reactant Jacobi coordinates system by using the Gaussian wave packet in the R direction, and it can be expressed as

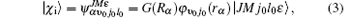
where ϕ v0j0(rα ) presents the rovibrational eigenfunction of the H2 molecule, |JMj0l0ε 〉 is the SF rotational basis, which describes the angular motion with M being the projection of the total angular momentum J, v0, and j0 are, respectively, the initial vibrational and rotational quantum number of H2 molecule, α and the hereinafter β are the label for the reactant and product channels, respectively.

After the preparation of the initial wave packet on the CPU in the SF reactant Jacobi coordinate, this wave function can be manipulated in BF product Jacobi coordinates by a split-operator scheme, entirely on GPU, and defined as[17]

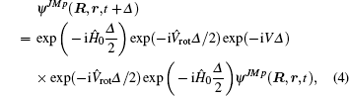
where

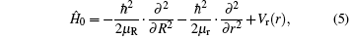
with .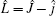

In the BF representation Jacobi coordinates, the scattering matrix element can be obtained as[17, 37]

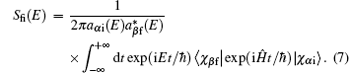
The coefficients are given by

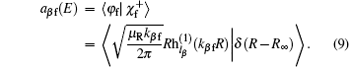
Here, φ i and φ f are the initial and final free wave functions, | χ f〉 = δ (R − R∞ )φ vfjf(rβ )|JMjflf〉 represents the radial component of the product wave-packet, R∞ is the location of the dividing surface, h(1) and h(2) are the spherical Hankel functions of the first and the second kind.[38]

Finally, the scattering matrix is transformed into a helicity representation to derive differential and integral cross sections by scattering matrix summing over all relevant values of the total angular momentum quantum number J, and they are expressed as

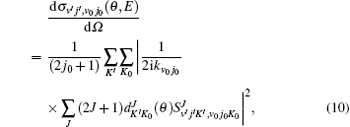
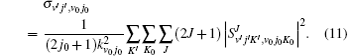
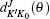
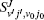
Here, θ is the scattering angle between the incoming N + H2 reactants and the scattered NH + H products, kv0j0 is the initial wave vector for the reactant, is the reduced rotation matrix with K0 and K′ being the projection of the initial and final total angular momentum J, is the S-matrix for transitions from initial vibrotational level v0j0 of the H2 molecule to final levels v′ j′ of the product NH molecule at an incident energy E.

3. Results and discussion
3.1. Numerical aspects

To obtain the converged results, many convergence tests are carried out for J = 0 to determine the optimal numerical parameters, which are summarized in Table  1. Meanwhile the state-to-state calculations for all values of angular momentum J up to 50 are conducted to obtain the convergent integral cross sections (ICSs) of the N(4S) + H2(X1Σ + ) → NH(X3Σ − ) + H(2S) reaction for collision energies up to 2.0  eV. In this work, K is one of the key convergence parameters, which sets an upper limit on the helicity quantum number. The convergence tests are shown in Table  2. It can be seen that for the selected J and higher collision energy Ecol = 1.92  eV, the number of K (K = min (14, J + 1)) is sufficient to yield converged results. In this paper, we only focus on the lowest reactant state H2 (v0 = 0, j0 = 0), which is sufficient to compare with the experimental results.

Table 1. Parameters used in the time-dependent wave packet calculations (All parameters are in atomic unit a.u. unless otherwise stated).
Table 2. Convergence test of N + H2(v0 = 0, j0 = 0) → NH(v′ , j′ = 0) + H reaction probabilities as a function of K (with Ecol = 1.92  eV, J = 30 and 40).
3.2. Total reaction probabilities and rate constants

In Fig.  2, we display the total reaction probabilities each as a function of the collision energy for several partial waves, which are only obtained by one of the open product channels, because of their symmetry characteristics of the N(4S) + H2(X1Σ + ) → NH(X3Σ − ) + H(2S) reaction. It can be clearly seen that with the increasing of J, the threshold energy shifts toward the higher collision energy. This behavior is apparently due to the centrifugal barrier which is increased with increasing J. The threshold energy of the J = 50 partial wave is approximately 2.0  eV. This demonstrates that the convergence of the J values is equal to 50 in this present collision energy range for calculating the cross sections. For the J = 0 partial wave, the threshold energy is equal to 1.13  eV, which agrees well with the forward barriers of the ground-state reaction reported to be 1.09  eV (25.1  kcal/mol).[4] We also calculate the initial state-selected reaction cross section as a function of the collision energy, which is shown in Fig.  3. Because of the existence of the potential barrier, the integral cross section displays a certain threshold energy, which increases monotonically with the energy. This behavior corroborates that the title reaction, which takes place via an abstraction mechanism, [4] is an endothermic reaction.

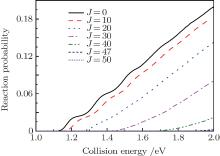Fig.  2. Total quantum scattering reaction probabilities each as a function of the collision energy for the N(4S) + H2(X1Σ + ) → NH(X3Σ − ) + H(2S) reaction at several values of J.

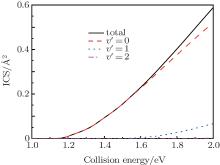Fig.  3. Total integral cross sections (ICS) and product vibrational state distributions each as a function of the collision energy for the N(4S) + H2(v0 = 0, j0 = 0) → NH(v′ , j′ = 0) + H reaction.

Considering the collision energy range studied, we plot the rate constants only in a temperature range of 1300  K– 4000  K in Fig.  4. The initial state-specific thermal rate constant is obtained from the integration of the integral cross section. The available experimental data and theoretical results of QCT and other theories [4– 6, 8, 39] are also shown in this figure. It is clear that our results based on the accurate state-to-state calculation agree well with the computational data of Pascual et al.[8] by using the QCT method, while the other results are smaller than our ones. The underestimation of other results can be attributed to the fact that the anharmonic effect is not considered in the improved canonical variational theory (ICVT) results.[40] Since the QCT results of Pascual et al.[8] have been proved to be in reasonable agreement with experimental measurements, a minor disagreement between our results and the QCT ones is also acceptable.

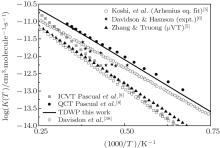Fig.  4. Rate constants in a temperature range of 1300  K– 1400  K. Also shown are the available experimental data and results of QCT and other theories.

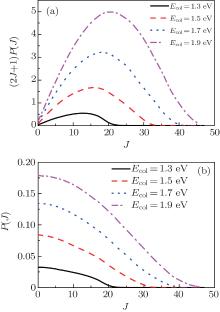
In order to clarify the J dependence of the total reaction probabilities, we plot the reaction probabilities each as a function of total angular momentum at four different collision energies in Fig.  5. From Eq.  (11) we can find that the J-dependent partial wave contribution to the integral cross sections is weighted over a 2J + 1 factor. As can be seen from Fig.  5(a) that for Ecol = 1.3  eV, this distribution, which is arch-shaped approximately, increases with J, reaches a maximum at a certain J and then decreases to zero before reaching the last available value of J. With the increase of collision energy, a marked shift of the most populated J for integral cross section occurs towards larger J values. As is well known, the J dependence of the total probability is an analogue of the classical opacity function, i.e., the reaction probability is a function of the impact parameter. Thus different J dependence means different impact parameter dependence. According to the above description, for the N(4S) + H2 abstraction reaction, two reaction mechanisms are proposed: a rebound mechanism and a stripping mechanism. The rebound collisions can be associated with small impact parameter collisions and lead to a backward scattering, while the striping scatterings correspond to the relatively large impact parameter collisions and tend to produce the forward and sideways scattering.[41] In order to see more clearly the reaction mechanism of the N(4S) + H2 reaction, we also plot Fig.  5(b). From Fig.  5(b), we can clearly see that at lower collision energies the populated J values for reaction probabilities mainly focus on the small values, and as the collision energy increases, the contributed value range of J is gradually enlarged. Based on the above descriptions, we can predict that the backward scattering is predominated at low collision energies by the rebounding collision mechanism, and the sideways and forward scatterings are dominant at high collision energies by the stripping collision mechanism.

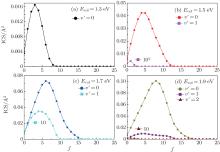
Fig.  5. (a) 2J + 1 weighted opacity functions and (b) total reaction probabilities for the N(4S) + H2(X1Σ + ) → NH(X3Σ − ) + H(2S) reaction at selected collision energies of 1.3, 1.5, 1.7, and 1.9  eV each as a function of the total angular momentum J.

3.3. Product state distributions

Figure  3 also displays the NH vibrational distributions of the N(4S) + H2(X1Σ + ) → NH(X3Σ − ) + H(2S) reaction in the 4A″ state, which are obtained by summing all available rotational state populations in each open vibrational channel. From this figure, we can see that the products NH molecules are almost in the ground vibrational state, until the collision energy increases up to 1.6  eV, the excited vibrational state products begin to appear. This behavior can be attributed to the endergonic reaction. Considering the collision energy we investigated, the NH product is found to be predominantly in v′ = 0 and v′ = 1 states. While with the increasing of collision energy, the increasing amplitude of the ICSs in the v′ = 1 state are less than in the v′ = 0 state.

Figure  6 displays the product rotational state distributions each as a function of the NH rotational quantum number j′ at several selected collision energies Ecol = 1.3, 1.5, 1.7, and 1.9  eV. This figure shows that the rotational excitation is very high for v′ = 0, and considerably drops for v′ = 1. Compared with the product vibrational distributions, the rotational states of the NH product are inverted at all vibrational levels for the four different collision energies. Obviously, the integral cross section maximum shifts toward higher j′ values and the amplitude of the maximum increases with the increase of collision energy. At Ecol = 1.3  eV, for instance, the NH rotational distribution for v′ = 0 peaks at about j′ = 3 with a cross section of 0.0164  Å 2. This peak shifts toward j′ = 8, with a corresponding increase in cross section about 0.10  Å 2, when Ecol = 1.9  eV. More rotational channels effectively open at high collision energies. This behavior can be attributed to the occurrence of the sideways and forward scattering, [42] which can cause the products to obtain the rotational energy. The larger the collision energy of the reactants, the larger the rotational energies of the obtained product are, and the corresponding rotational quantum number also becomes larger. From the point of view of the conservation of total angular momentum, [43] a lower impact parameter collision tends to produce the rotational cold NH products, which are usually corresponding to backward scattering. Similarly, large impact parameter collision between the N and H– H molecule usually leads to rotationally excited products, which are associated with sideways and forward scattering. Based on the above descriptions, we can also predict that the title reaction is almost dominated by the backward scattering at lower collision energies, while with the increasing of collision energy, the sideways and forward scatterings appear and increase.

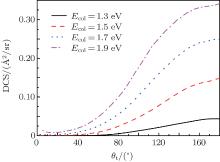
Fig.  6. Product rotational state distributions for the N + H2 (v0 = 0, j0 = 0) → NH(v′ , j′ ) + H reaction, at four different collision energies. Curves representing the case of v′ = 1 and v′ = 2 are multiplied by factors of 102, 10, and 10 for the collision energies of 1.5  eV, 1.7  eV, and 1.9  eV, respectively.

3.4. Differential cross sections

The total differential cross sections (DCS) of the N + H2 (v0 = 0, j0 = 0) reaction at four different collision energies of 1.3, 1.5, 1.7, and 1.9  eV each as a function of the scattering angles are shown in Fig.  7. At lower collision energy of 1.3  eV, the products NH molecules experience almost exclusively backward scattering with only minor components being forward scattered. Near the threshold energy value, our result is larger than the result of Zhang and Dong.[15] This behavior can be attributed to the omissions of the zero-point energy and the tunneling effect in the QCT method. As the collision energy increases, both the backward and forward scatterings increase. The above descriptions are in accordance with our expected results from the quantum opacity function. As mentioned in Subsection 3.3, the backward scatterings often occur at small impact parameters, while for the forward and sideways scatterings, more reactive collisions with larger impact parameters contribute. So the increases of forward and sideways scattering products are due to the participation in larger impact parameter collisions as the collision energy rises. For the H + HCl reaction and its isotopomers, a similar phenomenon was also found.[41] Backward scatterings in the A + BC abstraction reactions are often associated with a rebound mechanism and the forward and sideways scatterings indicate a striping mechanism. Based on the above statement, thus we come to a conclusion that at lower collision energies, the reaction is predominated by the rebound reaction mechanism, while for the high collision energies both stripping and rebound mechanisms coexist.

Fig.  7. The total differential cross sections for the N(4S) + H2(X1Σ + ) → NH(X3Σ − ) + H(2S) reaction at four collision energies.

4. Conclusions

An efficient GPU version of the TDQWP code is employed to study the

reaction on the novel 4A″ PES constructed by Zhai et el. In this work, we present the total and state-to-state integral cross sections and differential cross sections of the title reaction at collision energies up to 2.0  eV. The total integral cross sections increase monotonically with the collision energy rising, while there exists a threshold energy due to the existence of the potential barriers at the exit channel. These results indicate that the title reaction is an abstraction reaction. It is also found that the rotational distribution of the NH product is inverted in all vibrational states for our considered collision energies, while the vibrational distribution of the NH product is not. At low collision energies, the product NH is almost exclusively backward scattered with only minor components being forward and sideways scattered. With the increasing of the collision energies, the forward scattering is also increased slightly, which means both stripping and rebound mechanisms coexist in the case of high collision energies.

Acknowledgment

The authors thank Prof. Han Ke-Li for providing the computational codes.

Reference
1 Haynes B S 1977 Combust Flame 28 81 DOI:10.1016/0010-2180(77)90010-4 [Cited within:1]
2 Prasad K, Yetter R A and Smooke M D 1997 Combust Sci. Tech. 124 35 DOI:10.1080/00102209708935640 [Cited within:1]
3 Pederson L A, Schatz G C, Hollebeek T, Ho T S, Rabitz H and Harding L B 2000 J. Phys. Chem. A 104 2301 DOI:10.1021/jp9924575 [Cited within:1]
4 Koshi M, Yoshimura M, Fukuda K, Matsui H, Saitio K, Watanabe M, Imamura A and Chen C X 1990 J. Chem. Phys. 93 8703 DOI:10.1063/1.459257 [Cited within:6]
5 Davidson D F and Hanson R K 1990 Int. J. Chem. Kinet. 22 843 DOI:10.1002/(ISSN)1097-4601 [Cited within:1]
6 Zhang S W and Truong T N 2000 J. Chem. Phys. 113 6149 DOI:10.1063/1.1308544 [Cited within:3]
7 Takayanagi T, Kurosaki Y and Yokoyama K 2000 Chem. Phys. Lett. 321 106 DOI:10.1016/S0009-2614(00)00329-8 [Cited within:4]
8 Pascual R Z, Schatz G C, Lendvay G and Troya D 2002 J. Phys. Chem. A 106 4125 DOI:10.1021/jp0133079 [Cited within:5]
9 Poveda L A and Varand as A J C 2005 Phys. Chem. Chem. Phys. 7 2867 DOI:10.1039/b505590c [Cited within:3]
10 Yu X Y and Yu Y J 2013 Integr. Ferroelectr. 147 67 DOI:10.1080/10584587.2013.790743 [Cited within:2]
11 Zhang J, Chu T S, Dong S L, Yuan S P, Fu A P and Duan Y B 2011 Chin. Phys. Lett. 28 093403 DOI:10.1088/0256-307X/28/9/093403 [Cited within:1]
12 Zhai H S and Han K L 2011 J. Chem. Phys. 135 104314 1 [Cited within:8]
13 Morley C 1982 Combust Flame 47 67 DOI:10.1016/0010-2180(82)90089-X [Cited within:1]
14 Adam L, Hack W, Zhu H, Qu Z W and Schinke R 2005 J. Chem. Phys. 122 114301 DOI:10.1063/1.1862615 [Cited within:1]
15 Zhang J and Dong S L 2013 J. Chem. Sci. 125 895 DOI:10.1007/s12039-013-0429-3 [Cited within:3]
16 Anderson J A, Lorenz C D and Travesset A 2008 J. Comput. Phys. 227 5342 DOI:10.1016/j.jcp.2008.01.047 [Cited within:2]
17 Zhang P Y and Han K L 2014 J. Phys. Chem. A 118 8929 DOI:10.1021/jp5009779 [Cited within:4]
18 Ufimtsev I S and Martinez T J J 2008 Chem. Theor. Comput. 4 222 DOI:10.1021/ct700268q [Cited within:1]
19 Murrell J N and Carter S 1984 J. Phys. Chem. 88 4887 DOI:10.1021/j150665a016 [Cited within:1]
20 Varand as A J C and Poreda L A 2006 Theor. Chem. Acc. 116 404 DOI:10.1007/s00214-006-0092-6 [Cited within:1]
21 Chu T S and Han K L 2008 Phys. Chem. Chem. Phys. 10 2431 DOI:10.1039/b715180b [Cited within:1]
22 Lu R F, Chu T S, Zhang Y, Han K L, Varand as A J C and Zhang J Z H 2006 J. Chem. Phys. 125 133108 DOI:10.1063/1.2202826 [Cited within:1]
23 Harich S A, Dai D, Wang C C, Yang X, Chao S D and Skodje R T 2002 Nature 419 281 [Cited within:1]
24 Chu T S, Zahng Y and Han K L 2006 Int. Rev. Phys. Chem. 25 201 DOI:10.1080/01442350600677929 [Cited within:1]
25 Chu T S, Zhang X and Han K L 2005 J. Chem. Phys. 122 214301 DOI:10.1063/1.1924507 [Cited within:1]
26 Alexand er M H, Capecchi G and Werner H J 2002 Science 296 715 DOI:10.1126/science.1070472 [Cited within:1]
27 Xiao C L, Xu X, Liu S, Wang T, Dong W R, Yang T G, Sun Z G, Dai D X, Xu X, Zhang D H and Yang X M 2011 Science 333 440 DOI:10.1126/science.1205770 [Cited within:1]
28 Chu T S, Han K L, Hankel M, Balint-Kurti G G, Kuppermann A and Abrol R 2009 J. Chem. Phys. 130 144301 DOI:10.1063/1.3089724 [Cited within:1]
29 Gomez-Carrasco S and Roncero O 2006 J. Chem. Phys. 125 054102 DOI:10.1063/1.2218337 [Cited within:1]
30 Monge-Palacios M, Rangel C, Espinosa-Garcia J, Fu H and Yang M H 2013 Theor. Chem. Acc. 132 1349 DOI:10.1007/s00214-013-1349-5 [Cited within:1]
31 Peng T and Zhang J Z H 1996 J. Chem. Phys. 105 6072 DOI:10.1063/1.472444 [Cited within:1]
32 Althorpe S C 2001 J. Chem. Phys. 114 1601 DOI:10.1063/1.1334866 [Cited within:1]
33 Hankel M, Smith S C, Allan R J, Gray S K and Balint-Kurti G G 2006 J. Chem. Phys. 125 164303 DOI:10.1063/1.2358350 [Cited within:1]
34 Garcia E, Aoiz F J and Lagana A 2012 Theor. Chem. Acc. 131 1262 DOI:10.1007/s00214-012-1262-3 [Cited within:1]
35 Zhang P Y and Han K L 2013 J. Phys. Chem. A 117 8512 DOI:10.1021/jp400102r [Cited within:1]
36 Zhang J Z H 2009 Theory and Application of Quantum Molecular Dynamics Singapore World Scientific 37 [Cited within:1]
37 Dai J Q and Zhang J Z H 1996 J. Phys. Chem. 100 6898 DOI:10.1021/jp9536662 [Cited within:1]
38 Messiah A 1968 Quantum Mechanics New York John Wiley & Sons 56 [Cited within:1]
39 Davidson D F, Kohse-Hoingaus K, Chang A Y and Hanson R K 1990 Int. J. Chem. Kinet. 22 513 DOI:10.1002/(ISSN)1097-4601 [Cited within:1]
40 Truhlar D G, Isaacson A D and Garrett B C 1985 Theory of Chemical Reaction Dynamics Boca Raton CRC Press 65 [Cited within:1]
41 Song H W, Lee S Y, Sun Z G and Lu Y P 2013 J. Chem. Phys. 138 054305 DOI:10.1063/1.4790116 [Cited within:2]
42 Yao C X, Zhang P Y, Duan Z X and Zhao G J 2014 Theor. Chem. Acc. 133 1489 DOI:10.1007/s00214-014-1489-2 [Cited within:1]
43 Jankunas J, Sneha M, Zare R N, Bouakline F and Althorpe S C 2013 J. Chem. Phys. 138 094310 DOI:10.1063/1.4793557 [Cited within:1]