Since the detailed descriptions of the R-matrix method to deal with the electron– atom collision process have been presented elsewhere, ^{[24– 31]} a brief outline will be given here. This method begins by partitioning the subconfiguration space of the colliding electron into two regions by a sphere of radius a centered on the nucleus. The value of a is chosen such that the exchange interactions between the colliding electron and the other target electrons are negligible for r > a, where r is the distance of the colliding electron relative to the centroid of the target atom. Thus in the external region (r ≥ a), the colliding electron mainly feels a long-range static polarization potentials.

Within the reaction zone r ≤ a, the interactions between the colliding electron and the target electrons involve electron exchange and correlation interactions, which is a many-body problem and is solved variationally as a whole to obtain the logarithmic derivative boundary matrix R(E). Therefore, in the reaction-zone the electron correlations for the (N + 1)-electron system including the target atom and a colliding electron are calculated adequately by the variational method. The wavefunction Ψ for the (N + 1)-electron system of eigen-energy E in the reaction zone are expanded as

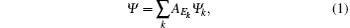
where Ψ _k are the energy-independent bases, which are expanded by the following way

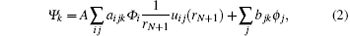
where A is the antisymmetrization operator which accounts for the electron exchange between the target electrons and the colliding electron. Φ _i are the channel wavefunctions obtained by coupling the N-electron target wave functions with the angular momentum and spin of the colliding electron. u_ij are the continuum orbitals. ϕ _j are (N + 1)-electron wave functions formed from the bound-type orbitals to ensure the completeness of the total wave functions and take account of the electron correlations within the reaction zone. The coefficients a_ijk and b_jk are obtained by diagonalizing the Hamiltonian matrix of the (N + 1)-electron system. Using the R-matrix method, we can deal with the interactions between the target electrons and the colliding electron in various channels within the reaction zone.

In an electron impact excitation process, the differential cross section dσ /dΩ is equal to (k′ /k)| f(k̂ ′ )| ² (atomic units are used throughout the paper if not specified). Here f(k̂ ′ ) is the scattering amplitude, which can be calculated by the following formula, ^[34]

where T_{i→ j} is the T-matrix. k (k′ ) and χ (χ ′ ) are the wave vector and spin wave function of the initial (final) state of the impact electron. Φ _i(L̃ S̃ π ̃ ) and Φ _j(L̃ ′ S̃ ′ π ̃ ′ ) are the initial- and final-state wave functions of the target with the definite angular momentum L̃ (L̃ ′ ), spin S̃ (S̃ ′ ), and parity π ̃ (π ̃ ′ ). | e^{ik· r}χ , Φ (L̃ S̃ π ̃ )〉 is the wave function of an (N + 1)-electron system. Ψ ⁺ characterizes the asymptotic behavior of the initial state for the (N + 1)-electron system. 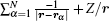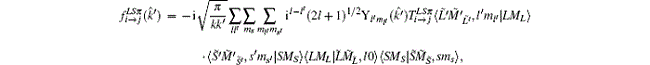V(r₁ … r_N, r) is the interaction operator between the impact electron and the target, which is equal to (Z is the charge of the atomic nucleus) if the interaction is Coulombic. N is the number of electrons in the target. r and r_α are, respectively, the coordinates of the impact electron and the α -th electron in the target relative to the centroid of the target. The partial wave scattering amplitude is

(4)

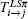
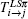
here the direction of incident electron is defined as the ẑ axis. l (l′ ) and s (s′ ) are the angular momentum and spin of the impact (scattered) electron. The total angular momentum L, spin S, and parity π of the (N + 1)-electron system are good quantum numbers in an electron impact process. are the reduced transition matrix elements in LSπ representation, which only connect the initial and final states with the same LSπ because of the conservation of the good quantum numbers. Moreover, are independent of the magnetic quantum numbers because of the rotational invariance of the scattering interaction. In this work, we adopt the set 2′ orbital basis of Ref. [20] to calculate the e– He collision excitation cross sections by the partial wave method using the FARM code.^[35] More specifically, the adopted orbital basis includes the spectroscopy orbitals nl (n = 1– 3, l = 0– 2) and the pseudo orbitals n̄ l (n̄ = 4– 6, l = 0– 4), and 11 physical states are used to expand the (N + 1)-electron system. The detailed description of the procedure to prepare the orbital basis and the convergence of the calculated total cross sections based on the basis can be found in Ref. [20]. In this work we only extend the calculations to a higher incident energy range.

According to Bethe theory, ^{[36, 37]} if the incident energy of the impact electron is high enough, the asymptotic wave function Ψ ⁺ of the (N + 1)-electron system can be evaluated by | e^{ik· r}χ , Φ _i(L̃ S̃ π ̃ )〉 within FBA, ^[38] and the corresponding FBA amplitude is

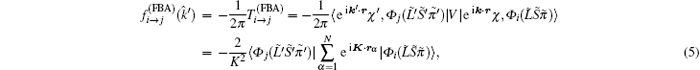
where is the T-matrix within FBA. K = k – k′ is the momentum transfer of the impact electron. In the last line of Eq. (5), the coordinate r of the impact electron is integrated^[38] and the infinite partial wave cross sections are calculated as a whole.

The generalized oscillator strength (GOS) F_{i→ j}(Δ E, K) of the target is defined as,

From Eq. (6), we can see that the accuracy of GOS is determined by the accuracy of the target wave function Φ (L̃ S̃ π ̃ ). Moreover, in the limit of K → 0, GOS is equal to the optical oscillator strength (OOS), which will be useful to test the accuracy of the calculated GOS by using the optical experimental measurement. In our previous work, ^[32] the high precision GOS of helium excited from the ground state to n¹S, n¹P, n¹D (n → ∞ ) and adjacent continuum states are calculated by using our developed codes.

Within FBA, the relation between the differential cross section and transition matrix is

After performing the summation of the final state and the average of the initial state, i.e. the integration of k̂ ′ , and the sum of M̃ ′ _{L̃ ′} , M̃ ′ _S̃ ′ , and m′ _s′ , and the average over k̂ , M̃ _L̃ , M̃ _S̃ , and m_s, we obtain the FBA total cross sections ,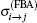

where [L̃ ] means 2L̃ + 1 and can be expanded as

According to the orthogonality of the Clebsch– Gordon coefficient and spherical harmonic functions, we obtain

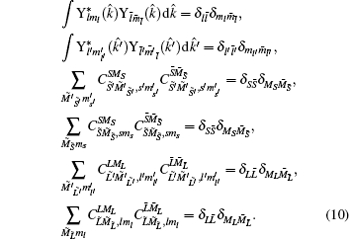
So the total cross section within FBA is

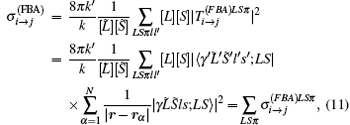
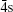
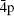
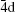
where γ represents all the other information to define the target state uniquely. Based on the traditional R-matrix codes we develop a new set of codes to calculate the PWCS’ s within FBA presented in formula (11). In this work, we adopt the same set of orbital bases, including spectroscopy orbitals 1s, 2s, 2p, 3s, 3p, 3d and pseudo-orbitals , , used in our previous helium GOS calculations, ^[32] to calculate the e– He collision excitation PWCS’ s within FBA by using our updated codes.

The difference between the exact PWCS and the FBA PWCS is

If decreases fast with the increasing angular momentum L, the convergent total cross sections can be obtained by the FBA total cross sections plus limited , i.e.

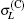
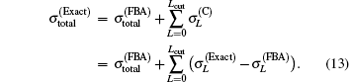
It means that a few lowest FBA PWCS’ s (L ≤ L_cut) of the total cross sections within FBA are replaced by the corresponding exact PWCS’ s. Beyond L_cut the difference between the exact and FBA PWCS’ s is negligible. This approach is anticipated to be more efficient than the partial wave method to calculate the total cross sections at intermediate incident energy, especially for the optical-allowed transition.

Figure 1 shows the comparisons between our calculated eight lowest PWCS’ s (L = 0 ∼ 7) for [1s²]1¹S → [1s2s]2¹S transition according to the formula (4) (labeled as “ Exact” ) and the formula (11) (labeled as “ FBA” ) respectively. In Fig. 1, it can be seen that the two kinds of PWCS’ s decrease fast with the increasing angular momentum L and the increasing incident energy. The maximum of the two kinds of PWCS’ s for L = 7 are only about 10% of those for L = 0 respectively. The two kinds of PWCS curves gradually merge together with the increasing L at the intermediate and high incident energies (> 200 eV). So the main contribution of the differences between and should originate from the several lowest PWCS’ s. In addition, it can be seen that the resonance structures mainly present in the low exact PWCS’ s with L ≤ 5 near the excitation threshold. No resonance structure appears in the FBA PWCS’ s.

Fig. 1.

	Figure Option ViewDownloadNew Window
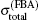
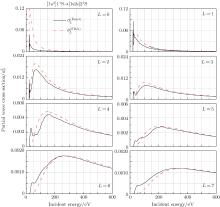	Fig. 1. The comparisons between the PWCS’ s (L = 0– 7) for [1s2]11S → [1s2s]21S transition calculated according to the formula (4) (solid line labeled as “ Exact” ) and the formula (11) (dashed line labeled as “ FBA” ) respectively.

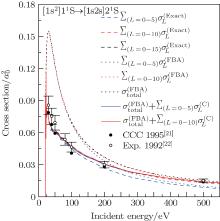
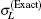
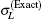
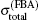
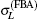
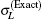
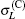
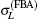
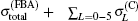
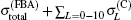
Figure 2 shows the total cross sections for [1s²]1¹S → [1s2s]2¹S transition calculated by partial wave method and FBA method respectively. In Fig. 2, at the low incident energies (from threshold to 50 eV) the blue, red, and black dashed lines (corresponding to the summations of the lowest 6, 11, and 16 respectively) nearly merge together; while at the higher incident energies, their difference becomes larger. It seems that the summations of 11 and 16 agree to the CCC results in the overall energy range while the summation of 6 is smaller at incident energies larger than 50 eV. This manifests that a convergence of the total cross sections near threshold (E_i < 50 eV) can be obtained by counting the lowest 6 PWCS’ s for the optical-forbidden transition, while at intermediate and high incident energies (E_i > 50 eV) 11 or even 16 PWCS’ s are necessary to be accounted. On the other hand, within FBA the summation of the lowest 11 is close to while the summation of the lowest 6 is lower than . At high incident energies (E_i > 400 eV), the summation of 11 and the summation of 11 merge together, which means the FBA is applicable here.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. The total cross sections for [1s2]11S → [1s2s]21S transition calculated by the different methods including the partial wave method (labeled as “ Exact” ) and the FBA method (labeled as “ FBA” ).

is the difference between and . In Fig. 2, the solid curves, corresponding to (blue) and (red) respectively, agree with our convergent results (the red and black dashed curves calculated by partial wave method). This means the approach to calculate the total cross sections at low to high incident energies, i.e., replacing a few FBA PWCS’ s (L < L_cut) of the FBA total cross sections by the corresponding exact PWCS’ s, is applicable for the monopole transition.

For more clarity, figure 3 shows the ratios of the calculated total cross sections by different methods in Fig. 2 relative to 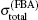. It is known that at the low incident energy the partial wave method is valid and at the high incident energy the FBA is applicable. In Fig. 3, near the excitation threshold the red solid line merges with the red dashed line (calculated by partial wave method), and at the high incident energy the red solid line is closest to one among all the lines, where one means being equal to the FBA results. Therefore, in the overall incident energy range, from threshold to high incident energies, the red solid line converges better than the other results obtained by partial wave or FBA method. This demonstrates that the approach, i.e., replacing the several lowest partial wave cross sections of the total cross sections within FBA by the corresponding exact partial wave cross sections, can deal with the electron impact excitation cross sections of atom for monopole transition from low to high incident energies in an efficient and consistent way. Moreover, the resonance structures are guaranteed since the main resonance features are kept in the lowest several exact PWCS’ s as shown in Fig. 1.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. The ratios of the calculated total cross section curves by the different methods in Fig. 2 relative to the total cross sections within FBA.

In Fig. 3, the blue dashed line (the summation of the 6 exact PWCS’ s) agree with the red solid lines in the range of E_i/Δ E < 3, the red dashed line (the summation of the 11 exact PWCS’ s) agree with the red solid lines until to E_i/Δ E ∼ 12. This demonstrates that at the high incident energies (E_i/Δ E > 12) more PWCS’ s need to be accounted for the total cross sections. The red and blue dotted lines (the summation of the FBA PWCS’ s) start from one at the threshold and then become lower than one gradually. This also means that with the increasing incident energies more FBA PWCS’ s need to be accounted for in the convergent FBA total cross sections.

Figure 4 shows the comparisons between our calculated eight lowest PWCS’ s (L = 0 ∼ 7) for [1s²]1¹S → [1s2p]2¹P transition according to the formula (4) (labeled as “ Exact” ) and the formula (11) (labeled as “ FBA” ) respectively. In Fig. 4, it can be seen that for L > 0 the two kinds of PWCS’ s decrease with the increasing L and the increasing incident energy. The FBA PWCS’ s decrease faster with the increasing L than the exact PWCS’ s. On the other hand, the FBA and exact PWCS curves gradually merge together with the increasing L in the overall energy range. 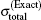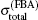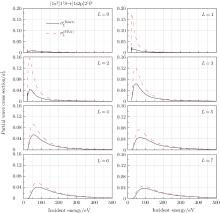Therefore, the main contribution of the difference between and should result from the several lowest PWCS’ s. Comparing with Fig. 1, the PWCS’ s for dipole transition decrease slower than those for monopole transition, which means the convergent process by using the partial wave method for dipole transition is slower than that for monopole transition, i.e., much more PWCS’ s need to be accounted for in the convergent total cross sections for dipole transition. In addition, in Fig. 4 the resonance structures mainly display in the exact PWCS’ s with L ≤ 3 near the excitation threshold, and no resonance structure appears in the FBA PWCS’ s.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. The comparisons between the PWCS’ s for [1s2]11S → [1s2p]21P transition calculated according to the formula (4) (solid line labeled as “ Exact” ) and the formula (11) (dashed line labeled as “ FBA” ) respectively.

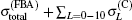
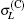
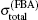
Figure 5 shows the total cross sections for [1s²]1¹S → [1s2p]2¹P transition calculated by partial wave method and FBA method respectively. In Fig. 5, it can be seen that in the whole incident energy range only the red solid line (i.e., ) agrees with the experimental measurement^[23] without missing the resonance structures and in a better degree than the CCC theoretical results^[21] at the intermediate incident energy around 100 eV. Therefore, the red line can be regarded as our convergent total cross section results. This means the approach of plus the summation of limited is applicable to calculate the excitation cross sections for dipole transition. The blue, red, and black dashed lines, i.e., the summations of the lowest 6, 11, and 16 exact PWCS’ s, agree with the red line only near the threshold and then deviate gradually. For instance, at 200-eV incident energy, the summation of the lowest 16 exact PWCS’ s is about 0.21, which is only about 66% of the convergent value 0.32. In fact, different from the fast convergence process of monopole transition, for dipole transition the convergence process is slow and it is difficult to obtain the convergent total cross sections by the partial wave method at intermediate and high incident energies. Near the threshold (about 21eV), the summations of the lowest 6 and 11 FBA PWCS’ s are initially close to and then become smaller than . At high incident energies (about E_i > 350 eV), the summations of PWCS’ s labeled by “ Exact” and “ FBA” merge together but are smaller than the FBA total cross sections.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. The total cross sections for [1s2]11S → [1s2p]21P transition calculated by the different methods including the partial wave method (labeled as “ Exact” ) and the FBA method (labeled as “ FBA” ).

To see this more clearly, figure 6 shows the ratio curves of the total cross sections calculated by different methods in Fig. 5 relative to . In Fig. 6, the red solid line is our convergent values. It is obvious that the blue dashed line (the summation of the lowest 6 exact PWCS’ s) agrees with the red solid line in the range of E_i/Δ E < 3. The red dashed line (the summation of the lowest 11 exact PWCS’ s) agrees with the red solid line till to E_i/Δ E ∼ 12, and for E_i/Δ E > 12 more higher PWCS’ s need to be accounted for the total cross sections. The ratios of the dotted lines (the summation of the FBA PWCS’ s) start from one and then deviate gradually. This feature means that with the increasing incident energies more FBA PWCS’ s need to be accounted for in the FBA total cross sections. On the other hand, with the increasing incident energies the dotted and dashed lines get closer to each other. In the high energy (E_i/Δ E > 30), the value of the red solid line is very close to one. Therefore, for dipole transition, at the intermediate and high incident energies the method of replacing the several lowest partial wave cross sections of the total cross sections within FBA by the corresponding exact partial wave cross sections is more efficient than the partial wave method. Moreover, this method guarantees the resonance structures near the excitation threshold and the satisfaction of FBA at high incident energies.

Fig. 6.

	Figure Option ViewDownloadNew Window
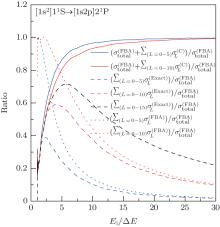	Fig. 6. The ratios of the calculated total cross section curves by the different methods in Fig. 5 relative to the total cross sections within FBA.