With the success of La@ C₆₀^[1] preparation, the experimental research has successively obtained K@ C₆₀, ^[2] He@ C₆₀, ^[3] and Ne@ C₆₀, ^[4] and so on. In such an environment, which is a double-well of the atomic potential, some novel properties of atoms appear. In the theoretical research of endohedrally confined atoms, ^{[5– 17]} only Connerade, ^{[7, 9, 11, 13]} Qiao, ^{[14– 16]} and Zhang^[17] have focused on their spectral properties. Meanwhile, some researchers have done some experiments on the spectral properties of endohedrally confined atoms.^{[18– 23]} In our work, a B-spline functions^[24] method is applied to calculate the energy level and the dipole oscillator strength of endohedrally confined helium, when the square potential well is changed into a parabolic potential one. The causes of the “ mirror collapse” and “ giant resonance” phenomena are analyzed.

This paper is organized as follows. In Section  2, the confined helium model and the B-spline functions are introduced. The results of energy levels and oscillator strength of the endohedrally confined helium are given in Section  3. This paper is closed by the conclusions in Section  4.

For a helium atom in an endohedral environment, the Hamiltonian is:

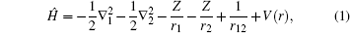
where V(r) is the attractive potential shell. In this paper, the shape of the attractive potential is changed to soften the endohedral environment. The attractive potential shell is defined as a parabola form

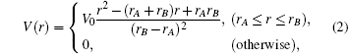
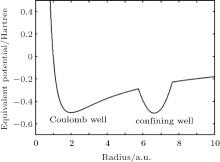
where the parameters r_A and r_B are the inner and outer radii of the confining potential well, and the values are 5.75  a.u. (the unit a.u. is the abbreviation of atomic unit) and 7.64  a.u., ^[25] respectively. In quantum mechanics, the equivalent potential of an electron is

Figure  1 shows the radial distribution of the equivalent potential of the ¹P₁ states. It is obviously a double well structure. The Coulomb well is called the inner well and the confining well is called the outer well. The parameter V₀ is the depth of the outer well.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Equivalent potential curve of the 1P1 state. The unit 1  Hartree = 27.2114  eV.

Normally, the radial wave-functions are expanded in three spatial ranges: 0 < r ≤ r_A, r_A < r ≤ r_B, and r_B < r ≤ ∞ . In this paper, B-spline functions are used to expand the wave-functions and the boundary conditions are satisfied very simply.

With the order k, the B-spline functions are defined as

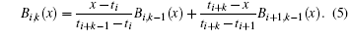
Here, {t_i} is the knots sequence set on the x axis. In our work, the order k is set to 7, so the knots sequence is

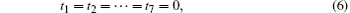
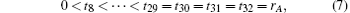
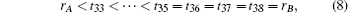
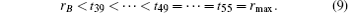
The basis set is

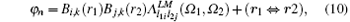
which is used to expand the wave-functions of the system. From the Schrö dinger equations, the matrix equation is obtained by

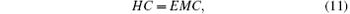
where H and M are respectively the Hamiltonian and overlap matrix. E and C are respectively the eigenvalues and eigenvectors, which can be obtained by solving the matrix equation  (11).

In quantum mechanics, the oscillator strength of a dipole transition is calculated by

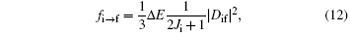
where Δ E = | E_f − E_i| , J_i is the initial state’ s total angular quantum number, D_if is the element of the dipole transition matrix and is defined by

As a consequence, for a specific dipole transition, the oscillator strength is determined by two terms: the energy difference and the square of the dipole transition matrix element.

By solving Eqs.  (1) and (11), the energy levels of the endohedrally confined helium have been calculated. In our work, 11760 basis sets are included in the expansion of the wave function. As a validation of the B-spline functions methods, we get the ground state energy to − 2.903703  Hartree in the case that the depth of the outer potential well is 0 Hartree. The reliability of the method was verified.

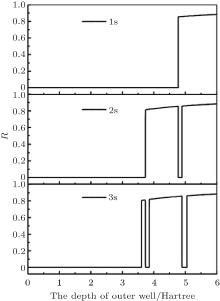
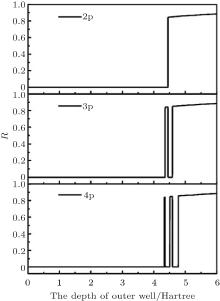
In our calculations, V₀ is taken from 0 to 6  Hartree in order to study the helium atom confined in buckminster fullerene more generally. The results of the calculation of the energy levels of the ¹S₀ and ¹P₁ states of a confined helium, as a function of the depth of the confining well, are shown in Fig.  2 and Fig.  3.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. 1S0 states’ energy levels for the helium confined in an attractive well, as a function of the depth of the outer well, with rA = 5.75  a.u. and rB = 7.64  a.u.

Fig.  3.

	Figure Option ViewDownloadNew Window
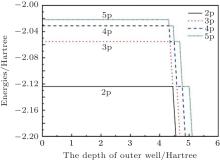	Fig.  3. 1P1 states’ energy levels for the helium confined in an attractive well, as a function of the depth of the outer well, with rA = 5.75  a.u. and rB = 7.64  a.u.

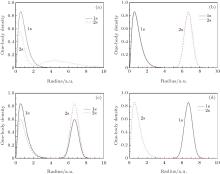
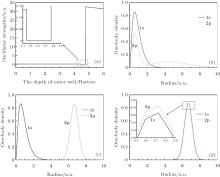
As shown in Fig.  2 and Fig.  3, the energy levels of the ¹S₀ and ¹P₁ states of helium reveal similar phenomena. Now, as an example, the ¹S₀ states are used to describe the phenomena. It can be seen that a few of ¹S₀ states hold the energies of an unconfined helium atom when V₀ is small. It seems that the outer confining well has no effect on them. The phenomenon can be understood by the distribution of the radial wave-functions of these ¹S₀ states. Figure  6(a) shows the one-body densities of the 1¹S₀ and 2¹S₀ states, which can represent the distributions of these states, with V₀ = 1.0  Hartree. This reveals that the radial wave-functions of these ¹S₀ states are almost zero in the range of the outer well. So the outer confining well has no effect on them. New ¹S₀ states emerge when the depth of the outer confining well continues to increase, and their radial wave-functions are distributed in the range of the outer well. Thus, new states are bound in attractive confining wells, but the original states are still bound in Coulomb wells. The new ¹S₀ states will change the existing energy sorting. For example, when a new 1¹S₀ state emerges, the original 1¹S₀ state will become a 2¹S₀ state, and 2¹S₀ states will become 3¹S₀ states, and so on.

In quantum mechanics, the condition that a system has bound states is that the depth of the confining well must achieve a certain value when the width of the confining well is fixed. In the double-well model, if the Coulomb potential is removed, the bound states will appear only when V₀ ≥ 1.018  Hartree. To understand the influences of the Coulomb potential and the attractive confined well for the system energies, we use Table  1 and Table  2 to show the relationship between them. In Table  1, the energies of ¹S₀ states of free helium, only confining attractive potential helium (Coulomb potential is removed) and double-well helium, are given respectively, with V₀ = 4.0  Hartree. The row of the 1¹S₀ state shows that the energies of the 1¹S₀ state of free helium and double-well helium are both − 2.9037  Hartree. It seems that the outer well has no effect on the 1¹S₀ state. However, the 2¹S₀ state of double-well helium is a new state, whose energy is − 2.3380  Hartree. This is the result of the cooperation of the Coulomb potential and the confining attractive potential.

Table 1.

Table 1.

Table 1. The energies of 1S0 states of free helium, only confining potential helium (Coulomb potential is removed) and double-well helium, with V0 = 4.0  Hartree. Orbitals Efree Econfined Edouble-well 11S0 − 2.9037 − 1.7368 − 2.9037 21S0 − 2.1459 − 1.6485 − 2.3380 31S0 − 2.0613 − 1.5263 − 2.2494

Table 1. The energies of 1S0 states of free helium, only confining potential helium (Coulomb potential is removed) and double-well helium, with V0 = 4.0  Hartree.

Table 2.

Table 2.

Table 2. The VCoulomb and Vconfined are expectations of Coulomb potential and confining an attractive potential with V0 = 4.0  Hartree. R is the ratio of the expectation of confining attractive potential to the expectation of total potential. Orbitals VCoulomb Vconfined R 11S0 − 6.753156 − 1.808361× 10− 11 2.677801× 10− 12 21S0 − 6.017686× 10− 1 − 2.862518 8.262936× 10− 1 1S0 − 6.0149648× 10− 1 − 2.8633745 8.264014× 10− 1

Table 2. The VCoulomb and Vconfined are expectations of Coulomb potential and confining an attractive potential with V0 = 4.0  Hartree. R is the ratio of the expectation of confining attractive potential to the expectation of total potential.

In Table  2, the V_Coulomb and V_onfined are expectations of Coulomb potential and confining attractive potential with V₀ = 4.0  Hartree, respectively. R is the ratio of the expectation of the confining attractive potential to the expectation of the total potential. R is calculated by

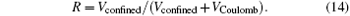
It can be seen that the Coulomb potential makes the major contribution to the 1¹S₀ state, and the confining attractive potential makes the dominant contribution to the 2¹S₀ state. So the 1¹S₀ state is the original state, and the confining attractive potential contribution can be ignored. The 2¹S₀ state is a new state, and the Coulomb potential contribution is relatively small compared with the confining attractive potential. It is worth noting whether it is a new or an original state, the energy is the result of the combination of Coulomb potential and confining attractive potential.

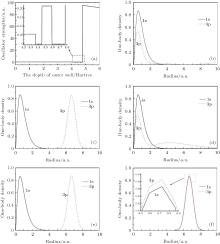
Now let us focus on the analysis of the ¹S₀ states. The 1¹S₀ state holds − 2.9037  Hartree, which is the 1¹S₀ state energy of an unconfined helium atom. The first ¹S₀ state energy line is a horizontal line, as the depth of the outer attractive well increases until its depth reaches to − 4.773  Hartree. Then, the 1¹S₀ state energy decreases very quickly, and its energy shows linear decreasing with the deepening of the outer confining well. To understand this phenomenon, the one-body density of the 1¹S₀ state is calculated, as a function of the outer attractive well. For V₀ = − 4.771  Hartree, the one-body density of the 1¹S₀ state is distributed around the nucleus, which indicates the first ¹S₀ state is a free helium ground state, which can be seen from Fig.  6(b). For V₀ = − 4.773  Hartree, the figure  6(c) shows that the one-body density of the 1¹S₀ state is distributed around the nucleus and the confining well, indicating that the 1¹S₀ state is the compound of a confining state and an unconfined helium ground state. In Fig.  6(d) with V₀ = − 4.775  Hartree, the one-body density of the 1¹S₀ state is distributed in the range of the outer confining well, indicating that the first ¹S₀ state is a bound state. The second ¹S₀ state has a similar behavior as the first ¹S₀ state has shown formerly. In Fig.  2, its energy holds − 2.1459  Hartree when V₀ is small, which is the value of the 2¹S₀ state energy of the unconfined helium, and the state stays in the Coulomb well. At the point V₀ = − 3.728  Hartree, the energy of the second ¹S₀ state suddenly decreases and continues to decrease with the deepening of the outer confining well till V₀ = − 4.773  Hartree. The state “ collapses” into the confining well. Then, when V₀ > − 4.773  Hartree, the state “ collapses” into Coulomb potential and stays there. At the point V₀ = − 4.891  Hartree, the state “ collapses” into the outer attractive well again and stays there finally. Some other ¹S₀ and ¹P₁ states’ behaviors have the same phenomena, which are shown in Fig.  2 and Fig.  3, respectively.

The phenomenon of “ collapse” can also be understood from the ratio of the expectation of the confining attractive potential to the expectation of the total potential. Figure  4 shows that the ratio R is very small for the 1¹S₀ state when V₀ is small, which implies that the Coulomb potential is dominant for the 1¹S₀ state. At the point V₀ = − 4.773  Hartree, the ratio R suddenly increases, which indicates that the 1¹S₀ state “ collapses” into the confining well. Then, the ratio R is a large value when V₀ ≥ − 4.773  Hartree, indicating that the outer attractive well is dominant for the 1¹S₀ state. The 2¹S₀ state’ s ratio reveals the same phenomenon. The ratio R is small when the 2¹S₀ state is bound in the Coulomb well, and it is very large when the 2¹S₀ state is bound in the outer well. At the “ collapse” point, the ratio R suddenly changes. The phenomenon also exists in other states of ¹S₀ and ¹P₁, which are shown in Fig.  4 and Fig.  5.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Ratio R of 1S0 states of the helium confined attractive well, changing the depth of the confining well. R is the ratio of the expectation of confined attractive potential to the expectation of total potential.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. Ratio R of 1P1 states of the helium confined attractive well, changing the depth of the confining well. R is the ratio of the expectation of confined attractive potential to the expectation of total potential.

Fig.  6.

	Figure Option ViewDownloadNew Window
	Fig.  6. One-body densities of the 11S0 and 21S0 states of endohedrally confined helium atom. The depth of an attractive well is: (a) V0 = 1.0  Hartree, (b) V0 = 4.771  Hartree, (c) V0 = 4.773  Hartree, (d) V0 = 4.775  Hartree, respectively.

At the “ collapse” point, V₀ = − 4.773  Hartree from Fig.  6(c), the first and the second ¹S₀ states are both strong mixtures of an unconfined helium state and a confined helium state, which leads to the result that their energy lines do not cross. Thus, at the avoided crossing point, V₀ = − 4.773  Hartree, the first ¹S₀ state suddenly “ collapses” into the outer confining well, which previously is bound in the inner Coulomb well. Simultaneously, the second ¹S₀ state “ collapses” into the inner Coulomb well, which previously is bound in the outer confining well. The behaviors of the ¹S₀ states are called “ mirror collapse.” Figures  2 and 3 show that other states also have the same phenomena. The point of avoided crossing is a cut-off point of the horizontal lines and the oblique lines, which reveals that those states are respectively bound in the inner Coulomb well and the outer confining well. It is worth noting that all oblique lines are parallel, which demonstrates that the energies of all states bound in the outer attractive well decrease at the same rate, i.e. at the same rate as the deepening of the outer well.

The ¹S₀– ¹P₁ dipole oscillator strengths of the endohedrally confined helium are calculated with Eqs.  (12) and (13) in our work. For a certain dipole transition, such as 1¹S₀– 2¹P₁ dipole transition, the energy difference is certain, so the dipole transition matrix element determines the oscillator strength. The dipole transition matrix element is related to the overlap of the wave-functions of the states involved in the transition. However, these wave functions are closely related to their one-body densities. So, the dipole transition matrix element is closely related to the overlap of one-body densities of the states involved in the transition.

The 1¹S₀– 2¹P₁ oscillator strengths are calculated and shown in Fig.  7(a) as functions of the depth of the confining potential well. When V₀ is a small value, 1¹S₀ and 2¹P₁ states are both bound in Coulomb potential and the overlap of one-body density of them is normal, so that the oscillator strength has the same value corresponding to that of an unconfined helium atom, which can be seen from Fig.  7(a) and Fig.  7(b). At V₀ = − 4.449  Hartree, the 2¹P₁ state collapses into the outer well, but the 1¹S₀ state is still bound in the Coulomb well. Then the oscillator strength suddenly decreases to a very small value from Fig.  7(a), but it is not zero. The reason is that the overlap of one-body densities of 1¹S₀ and 2¹P₁ states is close to zero from Fig.  7(c) with V₀ = − 4.6  Hartree. By increasing the depth of the outer well, when the depth V₀ = − 4.773  Hartree, the 1¹S₀ state collapses into the outer well. In this case, from Fig.  7(d) with V₀= − 4.9  Hartree, 1¹S₀ and 2¹P₁ states are all bound in the outer well so that their one-body densities overlap almost completely. So the value of oscillator strength is a large value, which is two orders of magnitude greater than the normal value of an unconfined helium atom. This phenomenon of very strong resonance enhancement of oscillator strength is called “ giant resonance.” At the same time, from Fig.  8(a), the 1¹S₀ and 2¹P₁ states are bound in the Coulomb well when V₀ is small, so the oscillator strength is normal. At the point V₀ = − 4.6  Hartree, the 1¹S₀ state is still bound in the Coulomb well, but the 2¹P₁ state is bound in the confining well. At that moment, the oscillator strength is very small. When V₀ ≥ − 4.773  Hartree, the 1¹S₀ and 2¹P₁ states are both bound in the outer well, the oscillator strength is enhanced and the phenomenon of “ giant resonance” appears. Not only the oscillator strength of 1¹S₀– 2¹P₁ dipole transition, but also other dipole transitions have the phenomenon about “ giant resonance, ” for example, 1¹S₀– 3¹P₁ dipole transition, 2¹S₀– 3¹P₁ dipole transition, and so on. Figure  9 shows the results of the oscillator strength of 1¹S₀– 3¹P₁ dipole transition and the corresponding one-body densities of 1¹S₀ and 3¹P₁ states in different depths of the outer attractive well. Figure  10 shows the results of the oscillator strengths of the dipole transitions of 2¹S₀– 2¹P₁ and 2¹S₀– 3¹P₁. Figures  8(b), 8(c), and 8(d) show the ratio R of states that are included in the dipole transitions, and corresponding to the 1¹S₀– 3¹P₁ dipole transition, 2¹S₀– 3¹P₁ dipole transition, and 2¹S₀– 3¹P₁ dipole transition, respectively.

Fig.  7.

	Figure Option ViewDownloadNew Window
	Fig.  7. (a) The 11S0– 21P1 oscillator strengths of confined helium with changing depth of outer confining potential well; inset shows the enlarged figure of the dotted box. (b)– (d) one-body densities of 11S0 and 21P1 states of endohedrally confined helium atom. The depth of an attractive well is: (b) V0 = 4.4  Hartree, (c) V0 = 4.6  Hartree, (d) V0 = 4.9  Hartree, respectively.

Fig.  8.

	Figure Option ViewDownloadNew Window
	Fig.  8. The ratio of the states involved in the dipole transition. (a) The dipole transition of 11S0– 21P1, (b) the dipole transition of 11S0– 31P1, (c) the dipole transition of 21S0– 21P1, (d) the dipole transition of 21S0– 31P1.

Fig.  9.

Figure Option ViewDownloadNew Window

Fig.  9. (a) The 11S0– 31P1 oscillator strengths of confined helium with changing depth of outer confining potential well; inset shows the enlarged figure of the dotted box. (b)– (e) one-body densities of 11S0 and 31P1 states of endohedrally confined helium atom. The depth of an attractive well is: (b) V0 = 4.3  Hartree, (c) V0 = 4.4  Hartree, (d) V0 = 4.5  Hartree, (e) V0 = 4.7  Hartree, (f) V0 = 4.9  Hartree, in which the inset shows the enlarged figure of the dotted box, respectively.

Fig.  10.

	Figure Option ViewDownloadNew Window
	Fig.  10. The 21S0 − 21P1 and 21S0– 31P1 oscillator strengths of confined helium with changing depth of the outer confining potential well; inset shows the enlarged figure of the dotted box. (a) The 21S0– 21P1 oscillator strength, (b) the 21S0– 31P1 oscillator strength.

The spectral properties of an endohedrally confined helium atom were calculated with the B-spline functions method. With the evolution of the energy spectrum as a function of the depth of the outer attractive well, the phenomenon of “ mirror collapse” exists in endohedrally confined helium. And the phenomenon of “ giant resonance” of the dipole oscillator strength appears with the increase of the depth of the confining well. These phenomena are due to the jumps of the wave-function between the Coulomb well and the confining attractive well, with the changing depth of the outer attractive well. It is readily apparent that the phenomena can also be understood from the major potential contribution changes between the Coulomb potential and the confining attractive potential, with the deepening of the outer attractive well.

The endohedral environment gives rise to some new questions about confined atoms. For example, the control of laser population, the prominent resonance in the photoionization cross section, and multiple photoionization, with endohedrally confined atoms.^{[26– 28]} Related work is being pursued.