†Corresponding author. E-mail: haipengren@gmail.com
*Project supported by the National Natural Science Foundation of China (Grant No. 61172070) and the Funds from the Science and Technology Innovation Team of Shaanxi Province, China (Grant No. 2013CKT-04).
In this paper, we propose a novel approach to secure communication based on spatiotemporal chaos. At the transmitter end, the state variables of the coupled map lattice system are divided into two groups: one is used as the key to encrypt the plaintext in the N-shift encryption function, and the other is used to mix with the output of the N-shift function to further confuse the information to transmit. At the receiver end, the receiver lattices are driven by the received signal to synchronize with the transmitter lattices and an inverse procedure of the encoding is conducted to decode the information. Numerical simulation and experiment based on the TI TMS320C6713 Digital Signal Processor (DSP) show the feasibility and the validity of the proposed scheme.
Since chaotic signals are irregular, aperiodic, uncorrelated, broad band, easy to generate, and difficult to predict over a long time, the secure communication based on these inherent features of a chaotic signal has aroused ongoing and growing research interest.[1]
Chaotic secure communication has received extensive attention since the possibility of synchronization of two coupled chaotic systems was reported in the early 1990s.[2– 6] The reported methods could be divided into three categories. 1) The methods use chaotic symbols to transmit information.[6, 7] The symbolic dynamics of a chaotic electrical oscillator is controlled to carry the message by using small perturbing pulses. 2) The methods use chaotic synchronization for secure communication. The methods of this kind can be divided into chaotic masking, chaotic modulation, and chaotic shift keying. Oppenheim et al. proposed chaotic masking, [8] and this method depends on the degree of chaotic synchronization and is susceptible to channel noise. Moreover, it is subjected to the attacking of time-delay embedded[9] and return map decoding.[10] Halle et al. suggested chaotic parameter modulation.[11] This method shows better performance than chaotic masking, but it is still sensitive to noise, and it could be attacked by nonlinear dynamic (NLD) forecasting techniques[12] and the time series analysis method.[13] Dedieu et al. proposed chaotic shift keying communication; [14] these secure communication schemes could be broken using the short-time zero-crossing rate, [15] spectrogram analysis, [16] generalized synchronization, [17] and adaptive key identification.[18] Thus, this method shows the weak security. 3) The methods use chaos asynchronous communication technology, such as chaos-based asynchronous code division multiple access (CDMA) systems, [19] direct sequence spread spectrum system.[20] These methods use chaotic series to replace pseudo-random code, have better performance than the traditional pseudo-random code. But the advantages of the chaotic signal, like broad band, orthogonality, etc. are not demonstrated in these methods. Since the chaotic communication has been reported to be successfully used in a commercial fiber optic channel to obtain a higher bit transmission rate, [21] chaotic communication research has gained more attention from the practical application viewpoint recently.[22– 25]
In this paper, we propose a novel approach to chaos communication based on spatiotemporal chaos. In this approach, the m-dimensional states of one-way coupled map lattices are divided into the two groups. One group is used as the inputs of the N-shift function to confuse m/2 plaintexts, then the outputs of the N-shift function are mixed with the other group of states to obtain the transmitted signals, which are used as not only transmission signals in the communication channel, but also the drive signals to synchronize the one-way coupled map lattices at the receiver end with those at the transmitter end. Once the synchronization between the receiver and the transmitter is established, the reverse operations at the receiver end will decode the transmitted information. This approach has three advantages: firstly, the spatiotemporal chaos system has the number of positive Lyapunov exponents equal to the dimension number of the system, which increases the randomness and unpredictability of the system. It is difficult to attack by using the time-delay embedded method. Secondly, the state variables of the coupled map lattice system are divided into two groups, one group is used as the inputs of the N-shift encryption function to encrypt the plaintext, and the other group is mixed with the outputs of the N-shift function to further confuse the information. Neither the key nor the plaintext transmits through the public channel, it will confuse the return map attacking. Thirdly, the chaos synchronization between the transmitter lattice and the receiver lattice is implemented by using similar drive signals, which are average values of the transmitted signal at the transmitter end and the received signal at the receiver end. The average operation acts as a filter to reduce the effect of noise on the synchronization, which makes the scheme possess better robustness to noise. Simulation and experiment based on TI TMS320C6713 show the feasibility and validity of the proposed scheme.
A spatiotemporal chaos system processes a mutual influence in both time and space, which is sensitive to initial conditions, boundary conditions, and parameter changes. The one-way coupled map lattice (OCOML) is a special case of the spatiotemporal chaos system.
The state equations of OCOML are
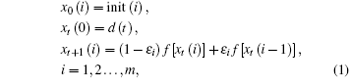
where t represents the discrete time, m is the space dimension number of OCOML, init(i) the initial value of the i-th lattice, ɛ i the coupling strength 0 < ɛ i < 1, xt(0) = d(t) the drive signal of the system, t = 0, 1, 2, … the discrete time, and f(x) a nonlinear chaotic map given by f(x) = 4x(1− x). The simulation result of this system is shown in Fig. 1, where i is the space position, t the discrete time, and xt(i) is the state of the i-th lattice at time t. The coupling strength used in Fig. 1 is ɛ i = 0.85 (i = 1, 2, … , m = 60). From Fig. 1, we see that the spatiotemporal chaos demonstrated by the OCOML is very complex, depending on both the time and space.
The transmitter OCOML is given as
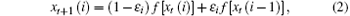
and the receiver OCOML is expressed as
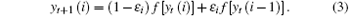
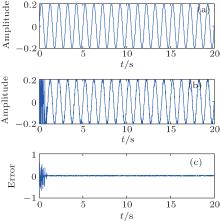
The dynamics of receiver system (3) is identical to that of the transmitter system (2). The receiver and the transmitter are synchronized under the same drive time series on the 0th lattice, in other words, if xt(0) = yt(0) = D(t), then the synchronization is achieved, where D(t) is a random or chaotic drive signal (series), t represents discrete time like that in Eq. (1). The drive series can choose and use (i) uniformly distributed random series; (ii) the series generated by a chaotic system. When we choose the uniformly distributed random series as the drive signal, the synchronization results of the two systems both with 15 lattices are shown in Fig. 2. The time series of the 10th lattice of the two systems are given in Fig. 2(a). The error of these states is given in Fig. 2(b). The square error sum of all the states of the lattices is defined as
The proposed secure chaotic communication scheme is shown in Fig. 3. There is an m-dimensional OCOML system at each of the transmitter end and the receiver end, and these two systems are referred to as OCOML-L and OCOML-R respectively.
At the transmitter end, the m-dimensional OCOML-L is given by Eq. (2), where ɛ i = 0.85, f(x) = 4x(1− x), and m is an even number.
The state variables of the OCOML-L are divided into two groups, and expressed as
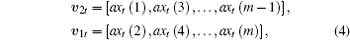
where xt(i) is the state variable of the i-th lattice at time t, and 0 < a < 1 is a constant gain. Plaintext frame with m/2 messages is given as follows:
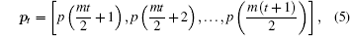
where t is corresponding to the discrete time of the OCOML-L. The plaintext vector pt is encrypted by vector υ 2t through using N-shift function e(pt, υ 2t), where N-shift cipher e(z1, z2) is defined as
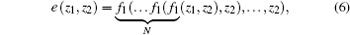
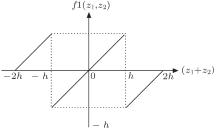
where f1(z1, z2) is given by
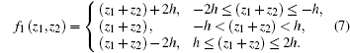
The relationship between input and output of f1(., .) is shown in Fig. 4.
An appropriate parameter h makes z1 and z2 be in the range (− h, h). The transmitted frame in the public channel is
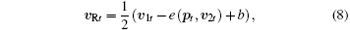
where 0 < b < 1 is a constant gain. The cryptograph frame is written as

The drive signal of the transmitter at moment t+ 1 is

So far, a plaintext frame has been encrypted by m state variables of the OCOML-L at time t.
At the receiver end, the transmitted plaintext can be recovered by using a reverse process of encryption. The m-dimensional OCOML-R is given by Eq. (3). Driven by the same signal, the OCOML-R and the OCOML-L will synchronize from any initial conditions after a transient state. The receiver is driven by
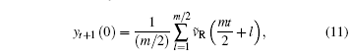
where 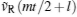

The recovered frame is
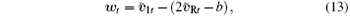
where
The plaintext can be decoded by N times iterations of the shift function (N-shift function), i.e.,

The values of N, h, a, b are the same as those used at the transmitter end. The 
From the above scheme, we know that the proposed method has the following features. Firstly, our method is different from those in Refs. [10] and [12], since our proposed secure communication system is based on hyper-chaotic spatiotemporal system. The spatiotemporal chaos system has positive Lyapunov exponents equal to the dimension number of the system, i.e., m. Therefore, the phase space of the signal would be very complex. It is difficult to attack by the time-delay embedded method.[9] Secondly, unlike using the XOR operation in Refs. [4] and [5] to encrypt the plaintext, a more complicated iteration, i.e., the N-shift function, is used in the proposed method, where the key is used to encrypt the plain signal through N-shift function. Since the N-shift function is a more complicated nonlinear function of the plaintext and the chaotic signal, it is very difficult to predict the plaintext from the output of the N-shift function. Thirdly, the key stream is transmitted in the public channel directly in Refs. [4] and [8], however, in our proposed method, neither the key nor the plaintext is transmitted directly in the public channel, which hides both the dynamical and the statistical characteristics of both chaotic key and plaintext. It would confuse the return map message recovery method.[10] Finally, the drive signal at the receiver end is an average value of m/2 transmitted data, which acts as a filter to reduce the effect of noise on the synchronization, which makes the scheme possess better robustness to noise as compared with a conventional synchronization method, for example, the method in Ref. [8].
In this section, we show the performance of the proposed secure communication scheme. In the following simulations, the following parameters are used: ɛ i = 0.85, a = 0.4, b = 0.4, h = 0.7, m = 10, and N = 30. In the first case, a sinusoidal signal is transmitted, the results are given in Fig. 5. The plaintext pt = 0.2sin(2π t) is given in Fig. 5(a); the transmitted signal is given in Fig. 5(b); the frequency spectrum of the transmitted signal is given in Fig. 5(c); the recovered signal is given in Fig. 5(d); the error between the plaintext and the recovered signal is given in Fig. 5(e).
From Fig. 5, we can see that the cryptographic signal is different from the original signal, and that the recovered signal is the same as the original signal. From Fig. 5(c), we know that the spectrum of the transmitted sinusoidal signal is fully embedded into the chaotic signal spectrum. From Fig. 5(d), we find that the plaintext is recovered after a transient state of synchronization.
In fact, the transmitted signal in a public channel is susceptible to the noise. The uniform distribution noise in the range (− 0.05A, 0.05A) (A is the amplitude of the transmitted signal) is incorporated into the transmitted signal. The simulation results are shown in Fig. 6, in which the transmitted signal, the recovered signal, and the error are given in Figs. 6(a), 6(b), and 6(c), respectively.
From Fig. 6, we see that the plaintext can be recovered even though the transmitted signal is polluted by the noise. Although the noise pollutes the recovered signal, one can reduce the influence through some simple low-pass filters.
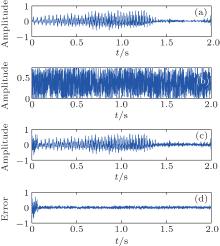
In the second case, the proposed scheme is also used for secure voice communication. There exists uniform distribution noise with the amplitude less than 10% of transmitted signal amplitude in the received signal. The result is shown in Fig. 7, where the plaintext signal is shown in Fig. 7(a), the signal in the communication channel is shown in Fig. 7(b), the recovered signal is shown in Fig. 7(c), the error between the recovered signal and the corresponding plaintext are given in Fig. 7(d). From Fig. 7, we see that the recovered signal is similar in wave form to the transmitted signal, and that the recovered voice is intelligible to be the same as that transmitted.
The experimental implementation of the proposed communication scheme is conducted using two floating-point DSPs, i.e., the TMS320C6713 develop starter kit (DSK) board. The block diagram of the experiment is given in Fig. 8. At the transmitter end, the voice signal is sampled by the embedded analog-to-digital (A/D) converter on a DSK board. The sampled signal is encrypted by the proposed algorithm, then the encrypted signal is transmitted through a multichannel buffered serial port (MCBSP) (a kind of series communication channel in the DSP chip) to the receiver end. At the receiver end, the received signal is used to decrypt the plaintext in DSP and replay them through the digital-to-analog (D/A) converter and the speaker.
 | Fig. 8. Block diagram of the experimental setup for demonstrating the proposed secure communication scheme. |
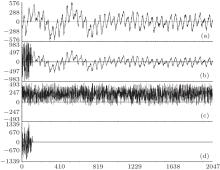
The experiment results are given in Fig. 9. The plaintext signal is given in Fig. 9(a); the recovered signal is given in Fig. 9(b); the cryptograph signal is given in Fig. 9(c); the error between the plaintext signal and the recovered signal is shown in Fig. 9(d). The experimental results show the feasibility of the proposed method.
The OCOML system processes a mutual influence between lattices both on time and space, and it is sensitive to initial conditions, boundary conditions, and parameter changes. These features contribute to security communication. In this paper, we propose a novel approach to secure communication based on such a spatiotemporal chaos. The state variables of the coupled map lattice system are divided into two groups and are used as the key to encrypt the plaintext. Neither the key signal nor the plaintext is directly transmitted in the public channel, which hides both the dynamical and the statistical characteristics of both chaotic key and plaintext. The level of security is enhanced. The proposed communication scheme is testified by DSP. The future work will be programming a secure exchange software based on the Android operation system to improve the security of personal cell phone communications.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|