†Corresponding author. E-mail: tiangs@pku.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant No. 11374017).
In this paper, we investigate the effect of the Coulomb interaction between electrons on the stability of Majorana fermion in a heterostructure of s-wave superconductor and quantum wire. In particular, by using the bosonization method and the renormalization group technique, we show that interplay between the so-called umklapp electron–electron scattering process and the superconducting proximity effect plays an extremely important role in determining the phase diagram of the system. We find that, at half-filling, the strong umklapp scattering process suppresses not only the superconducting pairing interaction and hence, destabilizes Majorana fermion in the quantum wire, but aslo results in a Mott insulating state. However, if the proximity effect is sufficiently strong, the topological superconducting phase can still survive and support Majorana fermion in the heterostructure. Furthermore, the existence of a critical Luttinger liquid phase is also found in a narrow region of parameters.
The concept of Majorana fermion was proposed by Ettore Majorana in 1937.[1] By its definition, the anti-particle of a Majorana fermion is itself. Therefore, the particle must be electrically neutral. Originally, one took a neutrino for such a candidate. However, the anti-neutrino was experimentally observed later and turned out to be a different particle. Up to now, the existence of the Majorana fermion in reality is still a fascinating but unresolved problem.
On the other hand, it is well known in condensed matter physics that the low-lying excitations in solids behave usually like quasi-particles in a short period of time, according to Landau.[2] That made people pondering the possibility that the Majorana fermion may appear in some condensed matter systems as a quasi-particle. For instance, Ivanov proposed that a Majorana fermion-type of quasi-particle can exist in the vortex core of a p-wave superconductor.[3] During the past decade, this speculation has been greatly stimulated by research on topological insulators.[4, 5] By the theory of topological insulators, the surface state of a strong topological insulator can be thought of as a single Dirac cone in the simplest case.[6] Therefore, the spin of one moving electron will be coupled to its momentum, forming a helical band structure and reducing the degrees of freedom by one half. Theoretically, this helical band structure can be mapped into the spectrum of a spinless fermion system. If an s-wave superconductor is now put near such a topological insulator, it should lead to superconductivity in the surface of the latter by the so-called proximity effect.[7] However, unlike the previously known examples, the induced superconducting state is of p-wave ordering in this case, as pointed out by Fu and Kane.[8, 9] In other words, for a replacement of the genuine exotic p-wave superconductor, we can engineer one by putting a three-dimensional topological insulator and an ordinary s-wave superconductor in close proximity. Consequently, Fu and Kane suggested that the Majorana fermion should appear as the bounded state of zero energy in a heterostructure of topological insulator and s-wave superconductor. This proposal recently generated tremendous interest in search of the Majorana fermion in some artificially manufactured systems such as carbon nanowires, [10, 11] graphene, [12] the heterostructure of the magnetic quantum dot and s-wave superconductors, [13] the heterostructure of semiconductor films and s-wave superconductors, [14, 15] as well as the heterostructure of semiconductor wires and s-wave superconductors.[16, 17] An important common feature of these materials is that they possess a strong spin– orbit interaction which makes the spin and momentum of the electron coupled.
Among the above-mentioned systems, the heterostructure of quantum wire and the s-wave superconductor suggested by the authors of Refs. [16] and [17] seems the most promising one. This model is structurally very simple. It requires only four main ingredients: one quantum wire, the existence of strong electronic spin– orbit coupling in the quantum wire, the presence of an external magnetic field, and an s-wave superconducting film. As those authors argued, under appropriate experimental conditions, Majorana fermion-type of quasi-particles will appear at the ends of the quantum wire. Very recently, several groups carried out experimental verifications on this proposal.[18– 23] The initial results showed plausible evidences for the existence of the Majorana fermion in this system.[18]
However, from the theoretical point of view, there are still some ambiguities which should be clarified. For instance, the authors of Refs. [16] and [17] did not consider the effect of the Coulomb interaction on the stability of Majorana quasi-fermion in their pioneering works. More precisely, they assumed actually that the properties of charged carriers in the quantum wire can be described by Landau’ s Fermi liquid theory.[2] The defining feature of such a liquid is the appearance of discontinuity in the density of states at the Fermi surface. Obviously, this is an over-simplified picture. As is well known, the renormalization effects by the Coulomb interaction between electrons are extremely strong in a lower-dimensional many-body system. In particular, for a quantum wire, these effects can even change its physical properties qualitatively. As a matter of fact, the electron– electron interaction in a one-dimensional system easily destroys the discontinuity in the density of states at the Fermi surface of the charged carriers and replaces it with a power-law singularity.[24] Furthermore, any quasi-particle in this system is no longer a fermion. They are bosons, i.e., gapless collective sound modes. Such a quantum state is called Luttinger liquid in the literature.[25] Therefore, a natural question that arose is whether the Majorana fermion-type of quasi-particles can survive if the effects of the Coulomb interaction are taken into consideration.
This important issue has been previously addressed by several groups with a standard method, which is called “ g-ology” treatment.[26– 29] First, one classifies the electron scattering interactions with respect to the transferred momenta by them. Then, one uses the perturbative renormalization group method to determine their relevance to the low-lying excitation spectrum of the system. By applying “ g-ology” , these authors found that the Majorana fermion-type of quasi-particles at the ends of quantum wire is indeed stable in some region of parameters. Certainly, this result is very encouraging. However, for some technical reasons, they did not include a special type of electronic scattering process, i.e., the so-called umklapp process in their calculations. Since this scattering process competes strongly with the superconducting proximity effect, it can definitely destabilize the topological superconducting phase in the quantum wire and hence, diminish the chance for Majorana fermions to survive. Therefore, one would naturally wonder whether negligence of such a scattering process in calculation is justified. In the present work, we shall remedy this shortcoming.
In order to overcome technical difficulties and simplify our analysis, we shall combine “ g-ology” treatment with the bosonization method, which maps all the fermionic degrees of freedom in a one-dimensional system to some bosonic degrees of freedom, [30] in our analysis. It is based on the following fact that some interactions between particles are easier to treat in the bosonic representation than in the original fermionic one. With this approach, we study first the effects of the Coulomb interaction between electrons at commensurate fillings in detail. We find that the umklapp scattering can be indeed neglected in this case. However, the forward scatterings may suppress the formation of topological superconducting state and hence, give rise to a gapless Luttinger liquid phase in the quantum wire. Then, we consider the half-filling case, in which the umklapp scattering process becomes extremely important. We show that it may lead to either a gapless Luttinger liquid phase or a Mott insulating phase. But, by applying the renormalization group technique, we find that, if the proximity effect between the quantum wire and the s-wave superconductor is sufficiently strong, a p-wave superconducting phase can still prevail in the quantum wire. Consequently, the existence of the Majorana fermion at the ends of the quantum wire is stabilized, even if the umklapp scattering process is included.
This paper is organized as follows. In Section 2, we introduce the Hamiltonian of the heterostructure of quantum wire and s-wave superconductor. We derive its energy dispersion and determine the region of parameters in which a non-trivial topological superconducting state exists. In Section 3, we map the Hamiltonian to an effective model. Then, we show that the Majorana fermion-type of quasi-particles occurs at the ends of the quantum wire. In Section 4, we apply the bosonization technique to the effective Hamiltonian and analyze its phase diagram by the renormalization group method at different fillings. Due to the competition between the umklapp scattering interaction and the superconducting proximity effect in the quantum wire, we obtain a very rich phase diagram. It consists of three parts, i.e., a Luttinger liquid phase, a Mott insulating phase, and a topological superconducting phase. The latter exists only in a specific region of parameters. Finally, in Section 5, we summarize our main results in this work.
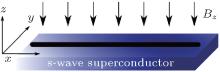
The layout of a heterostructure is shown Fig. 1. It consists of a quantum wire in proximity with an s-wave superconductor. To induce p-wave superconductivity in quantum wire, an external magnetic field is also introduced. For definiteness, the s-wave superconductor is laid flat on the xy-plane and the uniform magnetic field is perpendicular to its surface. Moreover, the quantum wire is placed along the direction of the x-axis. With respect to this setup, the Hamiltonian of the system can be written as
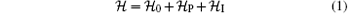
with

In 
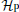
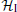


When B = 0, the single particle Hamiltonian 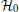
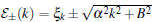
In the next section, we shall show that two (spinless) quasi-particles in the lower band can be paired with a p-wave ordering by Hamiltonian 
In order to make our analysis in the next section more readable, we shall give a brief review on the existence of the Majorana fermion in the above-mentioned heterostructure[16, 17] here.
For simplicity, we set the Coulomb interaction U to be zero in Hamiltonian (1). Therefore, electrons in the quantum wire can be treated as ideal fermions. Following Refs. [16] and [17], we write further the Hamiltonian of the heterostructure of quantum wire and s-wave superconductor into the Bogoliubov-de Gennes (BdG) form
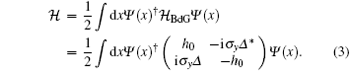
Here, 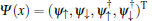

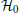

Here, we set ħ = 1. Hamiltonian (3) can be put into a more concise form

by introducing the Pauli matrices τ x, τ y, and τ z for the particle– hole degree of freedom in the system. By applying the standard Bogoliubov canonical transformation, we diagonalize 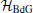
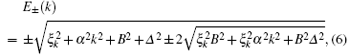
where k is the one-dimensional momentum of the electron in the quantum wire. This energy spectrum is plotted in Fig. 4. From the graph, we see that two energy gaps open up at points k = 0 and k = kF by the superconducting parameter Δ , which is induced by the proximity effect between the quantum wire and the s-wave superconductor. We shall denote these gaps by Δ E(0) and Δ E(kF), respectively. It is easy to see that, while Δ E(kF) does not vanish for any external magnetic field B, 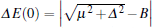
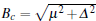
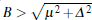
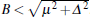
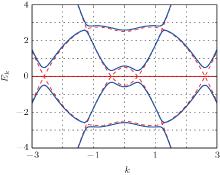 | Fig. 4. Energy spectrum of the spin– orbit interacting quantum wire with both magnetic field and proximity interaction. |
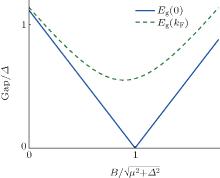 | Fig. 5. Variation of gaps Δ Eg(0) (the solid line) and Δ Eg(kF) (the dashed line) as magnetic field B changes. |
In the following, we shall concentrate on the case of large B. In other words, we assume that both conditions 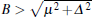
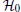

in which 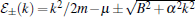
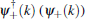
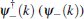
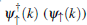
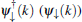
Next, we substitute this unitary transformation of fermion operators into Hamiltonian 


with
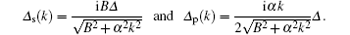
Interestingly, Δ s(k) and Δ p(k) can be thought of as the superconducting pairing amplitudes of quasi-particles. In particular, Δ p(k) yields a p-wave pairing in the quantum wire. In other words, a p-wave superconductor required for the existence of the Majorana fermion[3] may be realized in such a heterostructure of quantum wire and s-wave superconductor. Indeed, in the large-B limit, one can ignore the upper band in the spectrum of quasi-particles and keep only the contribution from the lower band. Consequently, the low-energy effective Hamiltonian of the quantum wire is given by

where μ eff = μ + B and m* = 1(1/m) – (α 2/B) are the effective chemical potential and mass of quasi-particles, respectively. Furthermore, the p-wave superconducting pairing amplitude is reduced to Δ p ≈ iα kΔ /2B in the large-B limit. Now, it is easy to see that 
When the length of the quantum wire is finite, the momentum of quasi-particle is no longer a conserved quantity. In this case, it is more convenient to re-write the effect Hamiltonian into a first quantization form. By dropping the lower band index of fermion operators, we obtain
It is actually the continuum version of the Kitaev chain Hamiltonian studied in Ref. [31]. This model can be exactly solved. One found that it possesses bounded states of zero energy at both ends of the quantum wire. These states behave like Majorana fermions. In other words, a nonzero p-wave pairing amplitude can induce Majorana fermion-type of quasi-particles in a one-dimensional spinless fermion system of finite length. Therefore, we conclude that Majorana fermions can survive in the quantum wire if the renormalized p-wave pairing amplitude by the additional Coulomb interaction between electrons is still nonzero. Otherwise, they are destabilized. It is this criterion by which we shall determine the stability of Majorana fermion in the following analysis.
With the above preparations, we are now ready to investigate the stability of Majorana fermion in the quantum wire when the correlation effects between electrons are taken into consideration. Naturally, parameter U is nonzero in this case and hence, Hamiltonian 
Since the quantum wire is a one-dimensional system, it makes application of the bosonization method possible. The motivation behind this approach is based on the fact that any low-energy excitation mode in a one-dimensional many-body fermion system can be taken as a superposition of collective bosonic sound modes.[24] In other words, a low-energy fermion state is equivalent to a coherent boson state in one dimension. Therefore, one expects that the fermion operator ψ (x) should be proportional to a coherent operator exp[iφ (x)], with φ (x) being a boson operator.[30] We would like to emphasize that this useful equivalence relation fails in higher dimensional space.
First, we apply the bosonization method to Hamiltonian (10) and re-write it with respect to the bosonic degrees of freedom. For this purpose, we need to linearize the Hamiltonian around the two Fermi points kF and − kF. Following the standard procedure given in Ref. [30], we expand the spinless fermion operator as
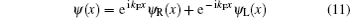
and then substitute it into Hamiltonian (10). It yields
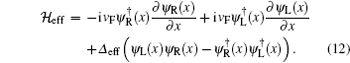
In this Hamiltonian, vF = kF/m* is the effective Fermi velocity and Δ eff = iα kFΔ /B. The fermions represented by 

Similarly, one can also linearize the interaction Hamiltonian 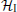
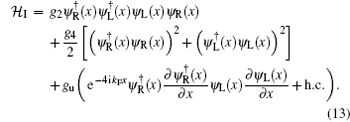
Here, parameters 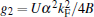
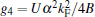
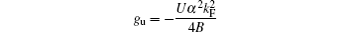
stands for the umklapp scattering process. The existence of factor e± 4ikFx in the gu-term makes it only important for the half-filling case, in which kF = π /2.
Next, as argued at the beginning of this section, we write the fermion operators in the form of bosonic coherent operators. For spinless fermion, the formula is well known.[30] We simply have
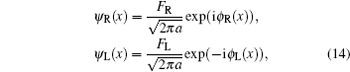
where ϕ R, L(x) are the corresponding boson field operators. Operators FR, L are called the Klein factors. They satisfy the fermion anti-commutation relations. Constant a denotes the microscopic distance cut-off, which is introduced to make each step of our calculations finite. In the final step, we shall let it tend to zero. Substituting Eq. (14) into Eqs. (12) and (13), we obtain the bosonized effective Hamiltonian of the interacting quantum wire as

in which the new boson field operators are defined by

These operators satisfy the commutation relation
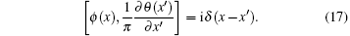
Therefore, operator Π ≡ (1/π )∂ xθ is defined to be the canonical momentum of ϕ (x). Moreover, parameter
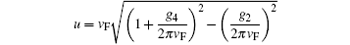
is the renormalized Fermi velocity and the dimensionless coefficient
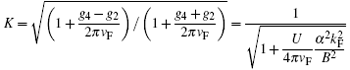
describes the interaction strength between quasi-particles. In particular, when the interaction is attractive, K > 1. Similarly, for the repulsive interactions, K < 1.
To determine the phase diagram of Hamiltonian (15), we apply the renormalization group analysis.[32, 33] The basic idea of this method is to integrate out the higher-energy degrees of freedom of a many-body system but keep the effects of virtual transition processes intact.[34] Following the standard procedure, we expand first the partition function of the system as

Here, operators 

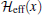
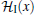
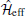
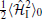
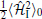
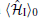
After a quite complicated but otherwise straightforward calculation, we obtain the following flow equations for parameters K, Δ eff, and gu
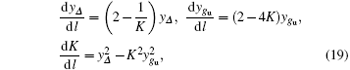
where 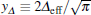

As argued above, the umklapp scattering interaction represented by gu can be neglected in this case since kF ≠ π /2. Therefore, by setting gu = 0, the above equations are reduced to
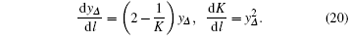
These equations have a trivial solution 
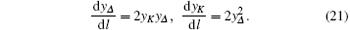
Multiplying the first equation by yΔ and the second one by yK, we can re-write these equations into
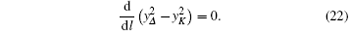
Therefore, we have solution 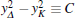
When the Coulomb repulsion between electrons is strong, i.e., K < 1/2, yK = 2K – 1 < 0 holds. In this case, there exist two possibilities. First, if the induced superconducting pairing interaction is weak such that parameter 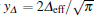

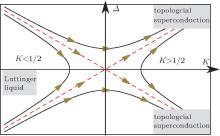 | Fig. 6. The RG flow trajectories of parameters in the case of non-half-filling. The phase diagram of the quantum wire consists of a Luttinger liquid phase and a topological superconducting phase, as obtained from Eq. (20). The origin point stands for (K = 1/2, Δ = 0). The blue line represents the attracting fixed points of Δ = 0, K < 1/2, which control the gapless Tomonaga– Luttinger liquid phase. The topological superconducting phase is characterized by the points, which flow eventually to Δ = ∞ or Δ = − ∞ . |
Next, we consider the case of K > 1/2. It indicates that the Coulomb repulsion between electrons is weak. Since parameter yK = 2K − 1 is now positive, the induced superconducting pairing interaction is relevant by the first equation in Eq. (21). Therefore, the renormalized parameters will flow to fixed points (yΔ = ± ∞ , K = ∞ ), which represent the existence of a topological superconducting phase.
Finally, we study the half-filled case, in which the umklapp scattering process between electrons plays an important role. Now, we need to solve the complete set of flow equations (19). These equations have two trivial solutions (K = 1/2, yΔ = ygu/2) and (K = 1/2, yΔ = − ygu/2), which represent two fixed points (or lines), respectively. As done above, we shall introduce new variables
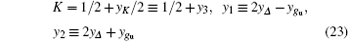
around these fixed points (lines) and re-write the flow equations as
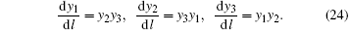
These equations can be easily integrated. For instance, if we multiply the first equation by y1 and the second one by y2, then their difference gives
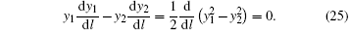
The integration of this equation is a constant. More precisely, we have
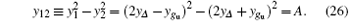
Similarly, we obtain also
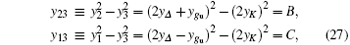
where B and C are integral constants. By varying constants A, B, and C, we can draw the renormalization group flow curves of yK, yΔ , and ygu in the three-dimensional parameter space. However, it is a cumbersome task. Therefore, we shall directly derive some important conclusions from these solutions without explicitly showing their diagrams.
First, we find the existence of two critical surfaces determined by equations B = 0 and C = 0, which can be put into a unified form
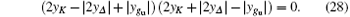
Consequently, the three-dimensional space of parameters is divided into two regions by a critical plane whose equation is

Since the flow curves of parameters do not cross the critical plane, we should separately study the properties of the system in these regions.
(i) In the region of 2yK + | 2yΔ | − | ygu| < 0, we need only to follow the flow curves with yK < 0. This is due to the fact that the flow equations (24) are established around the fixed lines (K = 1/2, yΔ = ygu/2) and (K = 1/2, yΔ = − ygu/2), on which | 2yΔ | − | ygu| = 0 holds. Therefore, each flow curve must pass a point with yK < 0 in this region. Following these curves, we see that, as yK → − ∞ , parameters | ygu| → ∞ and | yΔ | → 0. It implies that the superconducting pairing amplitude will be suppressed as the strength of the Coulomb repulsion between electrons gets stronger. Therefore, the quantum wire is a Mott insulator and Majorana fermion quasi-particles disappear at its ends in this region.
(ii) For the region in which 2yK + | 2yΔ | − | ygu| > 0, we follow the flow curves with yK > 0. As yK goes to infinity, we see that | ygu| → 0 and | yΔ | → ∞ . It tells us that, as the Coulomb repulsion gets weaker, the superconducting pairing interaction wins over. In the meantime, the umklapp scattering process becomes less important and can eventually be neglected. Therefore, the quantum wire is in a topological superconducting state, which supports Majorana fermions.
Special attention should be paid to the case of K = 1/2. By its definition, the initial value of parameter yK is now equal to zero, i.e., yK(0) = 0. Substituting it into Eq. (19), we find that both parameters yΔ and ygu become marginal. Therefore, if relation | 2yΔ (0)| − | ygu(0)| = 0 is initially satisfied, the flow curve will be completely contained in the critical plane and the system is in a gapless Luttinger liquid state. However, if the initial values of yΔ and ygu satisfy | 2yΔ (0)| > | ygu(0)| , then 2yK + | 2yΔ | − | ygu| > 0 holds. According to conclusion (i), it implies that, the superconducting pairing interaction is marginally relevant while the umklapp scattering process is marginally irrelevant under renormalization. Similarly, by conclusion (ii), if condition | 2yΔ (0)| < | ygu(0)| holds, the superconducting pairing interaction should become marginally irrelevant while the umklapp scattering process is marginally relevant under renormalization.
In summary, by renormalization group analysis, we find that, for K > 1/2, the umklapp scattering process can indeed be neglected. Therefore, the correlated quantum wire is still in a topological superconducting state and supports the Majorana fermion type of quasi-particles at its ends. However, when K < 1/2 holds, the superconducting pairing interaction becomes irrelevant and the umklapp scattering process will eventually prevail. Unlike the gapless Luttinger liquid state in the non-half filling case, it leads to a Mott insulating ground state, and hence, destabilizes the existence of the Majorana fermion in the quantum wire. Finally, the situation is rather complicated if K = 1/2. In this case, both the superconducting pairing interaction and the umklapp scattering process are marginal. Therefore, the quantum wire can be in either a gapless Luttinger liquid state, a topological superconducting state or a Mott insulating state, depending on the initial values of parameters yΔ and ygu.
In this paper, we studied the effect of the Coulomb interaction between electrons on the stability of the Majorana fermion type of quasi-particles in a heterostructure of quantum wire and s-wave superconductor. In particular, we consider the competition between the so-called umklapp electron– electron scattering process, which was neglected in some previous investigations, and the superconducting proximity effect in such a system. By applying the bosonization method and the real-space renormalization technique, we established first the flow equations satisfied by various coupling constants. Then, by solving these equations, we find that a strong umklapp scattering process can indeed subdue the superconducting pairing interaction in the quantum wire and lead to a Mott insulating state, which is quite different from the gapless Tomonaga– Luttinger liquid phase in the non-half-filled case. Naturally, that makes the Majorana fermion at the ends of the quantum wire vanish. However, if the proximity effect between the quantum wire and the s-wave superconductor is sufficiently strong, the topological superconducting ordering can still survive. Therefore, Majorana fermion quasi-particles are stabilized in the heterostructure. Moreover, we find also the possible existence of a gapless Luttinger liquid state in a narrow region of parameters for the system.
We would like to thank Dr. Chen Yu and Mr. An Wei for helpful discussions on several important issues.
In fact, parameter
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|