In the past decade, the control of quantum degenerate gases of ultracold atoms is widely studied by exploiting collisional resonances.^{[1– 4]} Many properties of ultracold gases depend on the s-wave scatting length.^{[5– 7]} Magnetic-field-induced Feshbach resonance (MFR) is an effective tool and has been applied widely to the research of alkali atomic gases to control the interaction between atoms.^{[8– 11]} However, MFR is limited in current experiments due to its relatively longer time scales and lower spatial resolution. An alternative way for modulating interatomic interactions is optical Feshbach resonance (OFR). In the OFR, a photoassociation light is employed to realize the transition from the continuum state of the colliding atomic pair to the excited molecular state.^{[12– 14]} Fatemi and co-workers^[15] observed optically induced Feshbach resonance in a cold (< 1  mK) sodium vapor. Based on the coherent free-bound stimulated Raman transition, Thalhammeret al.^[16] investigated optical Feshbach resonance in the ⁸⁷Rb Bose– Einstein condensate. OFR offers more flexible control over the interaction strength since the laser intensity can be changed on a small scale.^{[17– 19]} However, OFR often suffers from rapid loss of atoms due to the light-induced inelastic collisions between atoms which can be characterized by the two-body loss coefficient K₂.

Optical controls together with magnetic Feshbach resonances have been developed to modify the interatomic interaction. Bauer et al.^{[20, 21]} explored how to control the scattering length near the magnetic Feshbach resonance by driving an optical-induced transition between the ground state and excited molecular state. They demonstrated that a single-color laser light can not only noticeably shift an MFR but also reduce the rate of particle loss. Mackie^{[22, 23]} analyzed the role of quantum interference between magnetic and optical Feshbach resonances in cold atomic collision, and found that the quantum interference between photoassociation and Feshbach s-wave resonance could suppress inelastic and enhance the elastic scattering cross section. The improved quantum interference method was applied to the optical control with a wide tunability of scattering parameters.^[24]

In our previous work, ^[25] we theoretically demonstrated that a dark state formed by the coherent superposition of two ground-states of a molecule induced by two optical lasers can modulate the MFR and suppress the inelastic loss. In the present work, we propose an alternative scheme for controlling the scattering length with a two-color optical field. We focus our attention on how the two excited molecular bound states are to be coupled to the ground molecular bound state by two optical fields. The quantum interference of two molecular excited states is used to modulate the MFR and reduce the inelastic loss. A many-body approach is used to describe the optical modulation of MFRs in Bose gas. The analytical expressions of the scattering length are obtained by solving the Heisenberg equation. The influences of the two-color optical field on scattering length and two-body loss-rate coefficient are discussed.

Our control scheme involving four electronic states is shown in Fig.  1, where |a〉 represents the scattering continuum state. The hyperfine interaction can couple the scattering continuum state |a〉 ⊗ |a〉 of the open channel to a bound vibrational state |g〉 in the closed channel. The atom– molecule coupling between the atom-pair state |a〉 ⊗ |a〉 and the ground state |g〉 , which is related to the Feshbach resonance, is described by the coupling strength α . The two-color laser field couples the ground state |g〉 to the excited electronic states |e₁〉 and |e₂〉 . The two-color laser field modulated by two coherent and simultaneous pulses can be expressed as^[26]

where E₁ and E₂ are the field amplitudes, and ω ₁ and ω ₂ are the center frequencies of the fundamental fields. The Hamiltonian is written as^[25]

where the optical field-system interaction Hamiltonian is given by

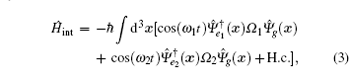
with (j = a, g, e₁, e₂) being the bosonic annihilation (creation) field operator. H_j is the single-particle Hamiltonian. x₁₂ = x₁ − x₂ is the relative coordinate and X₁₂ = (x₁ + x₂)/2 the center-of-mass coordinate. Ω ₁₍₂₎ = 〈 g|d|e₁₍₂₎〉 ε ₁₍₂₎/ħ is the Rabi frequency corresponding to the transition |g〉 → |e₁〉 (|g〉 → |e₂〉 ). Two-atom elastic collisions far away from the Feshbach resonance depends on U_bg and the atom– molecule coupling relevant to the Feshbach resonance is described by α (x₁₂). The molecule– molecule interactions are neglected due to the low density of molecules. Since the number of incoming particles in the gas is small enough, α (x₁₂) approximates to a constant α . We assumed that the population in each state is Bose-condensed and can be described by a mean field , j = (a, g, e₁, e₂). Taking the expectation value of the Heisenberg equation of motion and using the commutation relation of the annihilation and creation operator, we obtain the mean-field equation,

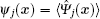
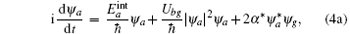
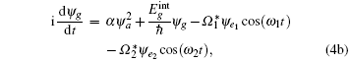
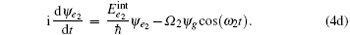
The single-particle Hamiltonian containing kinetic operator and internal energy is given by

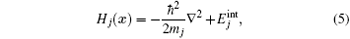
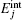
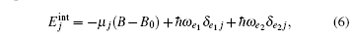
where m_j = m(2 − δ _aj) is the mass of atom in the state j and δ _ij is the Kronecker symbol. The internal energy depends nonlinearly on magnetic field B. In the vicinity of the position B₀ of Feshbach resonance, this dependence is linear and expressed as

where μ _j is the magnetic dipole moment. At B = B₀, the |a〉 and |g〉 states are degenerate, and the energy of the |e₁〉 (|e₂〉 ) state is ħ ω _e1 (ħ ω _e2).

Fig.  1.

Figure Option ViewDownloadNew Window

Fig.  1. A scheme for optical modulation of a Feshbach resonance with two-color optical fields. The two-color optical fields with frequencies ω 1 and ω 2 and Rabi frequencies Ω 1 and Ω 2 couple the ground states |g〉 to the excited states |e1〉 and |e2〉 , respectively. α denotes the coupling between the incoming atomic pair state |a〉 ⊗ |a〉 and |g〉 , which is responsible for a magnetically induced Feshbach resonance.

We now perform a transformation by ψ _e1 → φ _e1 e^{iω ₁t} and ψ _e2 → φ _e2 e^{iω ₂t}. By using the rotating wave approximation, equation  (4) can be written as

Furthermore, by taking

equation  (7) can be reduced to

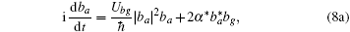
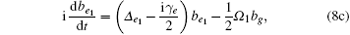
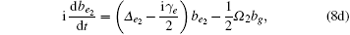
where γ _e is the decay rate resulting from spontaneous radiative decay from the |e₁〉 and |e₂〉 states to the states that are not included in the model. Δ _g, Δ _e1, and Δ _e2 are given by

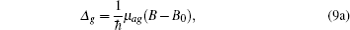
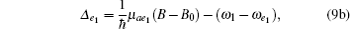
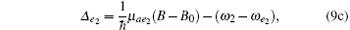
where μ _ag = 2μ _a − μ _g, μ _ae1 = 2μ _a − μ _e1, and μ _ae2 = 2μ _a − μ _e2. The adiabatic elimination is performed by setting (d/dt)b_g = (d/dt)b_e1 = (d/dt)b_e2 = 0. We can obtain the s-wave scattering length ã = a + ib by eliminating b_g, b_e1, and b_e2 from Eq.  (8), yielding

where a_bg is the background scattering length. For a pure Feshbach resonance (Ω ₁ = Ω ₂ = 0), equation  (11) is reduced to the well-known result of a magnetically induced Feshbach resonance:

with the resonance width

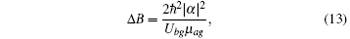
where |α | is the Feshbach strength. The real part a of the scattering length is responsible to the mean-field energy. The imaginary part b of the scattering length describes the two-body loss by rate equation

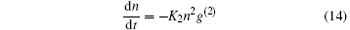
with

where n = |Ψ _a|² is the peak density of the Bose– Einstein condensate (BEC). g⁽²⁾ is the pair correlation function at zero relative distance. For a BEC with N atoms, g⁽²⁾ = 1 − 1/N.

Using the above theoretical approach, we study the two-color laser modulation of the magnetically induced Feshbach resonance. Table  1 shows the parameters used in the calculation for the ⁸⁷Rb which are taken from Ref.  [22]. Figure  2 displays the imaginary part of scattering length as a function of the detuning Δ _e1 and Δ _e2. We take Ω ₁ = 5γ _e, Ω ₂ = 3γ _e, and B − B₀ = 0.02  Gs in the calculation. By choosing the suitable Δ _e1 and Δ _e2, the imaginary part of scattering length b can be less than − 0.01. The suitable ranges of Δ _e1 and Δ _e2 are shown in Fig.  2.

Table 1.

Table 1.

Table 1. Numerical parameters used in the calculation for the 87Rb which are taken from Ref.  [21]. a0 is the the Bohr radius. The unit of μ ag/ħ , μ ae1/ħ , μ ae2/ħ , and γ e/ħ is MHz/Gs (1  Gs = 10− 4  T). The unit of |α | is mHz cm3/2. B0/Gs Δ B/Gs μ ag/ħ μ ae1/ħ μ ae2/ħ γ e/ħ abg |α | 1007.4 0.21 2π × 3.8 2π × 2.7 2π × 2.7 2π × 5.3 100.5a0 2π × 1.8

Table 1. Numerical parameters used in the calculation for the 87Rb which are taken from Ref.  [21]. a0 is the the Bohr radius. The unit of μ ag/ħ , μ ae1/ħ , μ ae2/ħ , and γ e/ħ is MHz/Gs (1  Gs = 10− 4  T). The unit of |α | is mHz cm3/2.

Fig.  2.

	Figure Option ViewDownloadNew Window
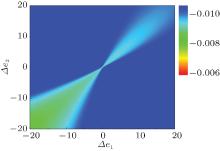	Fig.  2. The imaginary part of scattering length as a function of the detuning Δ e1 and Δ e2 in units of γ e.

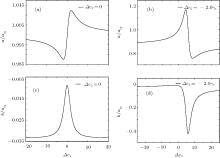
The change of scattering length with the photon detunings Δ _e1/γ _e is illustrated in Fig.  3. The parameters are chosen as before. For Δ _e2 = 0, there is one resonance at Δ _e1 = 0. For Δ _e2 = − 2γ _e the resonance takes place at Δ _e1 = 5.0γ _e. The imaginary part b displays a dispersive feature and the real part a is approximately described by the Lorentzian function. As shown in Fig.  3(b) and Fig.  3(d), the resonance position changes with Δ _e2. When Δ _e2 = − 2γ _e, the minimum of imaginary part b/a_bg appears at Δ _e1 = − 1.9γ _e, which means that the two-body loss reaches its minimum value. For Δ _e2 = 0, the imaginary part b/a_bg displays an opposite variation trend to that for Δ _e2 = − 2γ _e. The imaginary part b/a_bg = − 0.008 at Δ _e2 = 0, which is less than the value obtained in a single-color field. This means the two-color field can enhance the scattering length and reduce the loss by adjusting the detunings Δ _e1 and Δ _e2.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. The scattering length as a function of the detuning Δ e1 for Δ e2 = 0 and Δ e2 = − 2γ e.

Figure  4 shows the scattering lengths a and b in units of the background length a_bg as a function of the ratio K = Ω ₁/Ω ₂. Here B − B₀ = 0.02  Gs. For Δ _e1 = 2.5γ _e, Δ _e2 = − 2.5γ _e, and Ω ₂ = 2γ _e, a resonance is created at K = 0.9. For Δ _e1 = Δ _e2 = 2.5γ _e and Ω ₂ = 2γ _e, the real part a decreases rapidly with the increase of K. For different detunings, the imaginary part b displays two different variation trends. From Eq.  (15), we can see that the two-body loss coefficient K₂ is proportional to the absolute value of b. With the increase of K, the absolute value of b decreases up to 0.001. This means that we can reduce effectively the two-body loss coefficient K₂ by adjusting the ratio of the Rabi frequencies Ω ₁ and Ω ₂.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Scattering length as a function of the ratio K = Ω 1/Ω 2 for (a) Ω 2 = 2γ e, Δ e1 = 2.5γ e, and Δ e2 = − 2.5γ e, (b) for Ω 2 = 2γ e, Δ e1 = 2.5γ e, and Δ e2 = 2.5γ e. The black line shows the real part a/abg and the red line shows the imaginary part b/abg.

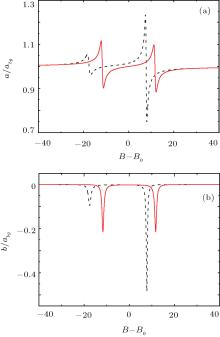
To explore the magnetic field dependence of the scattering length for fixed optical field parameters, we calculate the scattering lengths a and b as a function of B. The Rabi frequencies are fixed at Ω ₁= Ω ₂ = 10γ _e. As shown in Fig.  5, two resonances appear in a, and each of them displays approximately dispersive feature. From Fig.  5(a), we can observe two symmetrical splits around B₀ when ω ₁ = ω _e1 and ω ₂ = ω _e2, which are the well– known Auter– Townes doublet. When ω ₁ − ω _e1 = − 5γ _e and ω ₂ − ω _e2 = − 5γ _e, the two resonance positions appear at B − B₀ = 7.7  Gs and B − B₀ = − 17.5  Gs. In Fig.  5(b), the imaginary part b also displays two resonances. For different detunings, their heights, widths, and positions are quite different. When ω ₁ = ω _e1 and ω ₂ = ω _e2, we observe two symmetrical resonances at B − B₀ = 11  Gs and B − B₀ = − 11  Gs. When ω ₁ − ω _e1 = − 5γ _e and ω ₂ − ω _e2 = − 5γ _e, two resonances appear at B − B₀ = 7.7  Gs and B − B₀ = − 17.5  Gs. The bound-to-bound coupling can modify the energies of the bound levels. By changing the Rabi frequencies, the bound level crosses the atomic threshold of a different hyperfine level and new Feshbach resonance can be created. With the shift of the bound level the crossing position is also changed which means that by adjusting the parameter of the light, we can modify the Feshbach resonance.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. (a) The real part a/abg of the scattering length as a function of the magnetic field B − B0 for fixed optical field. (b) The variations of imaginary part b/abg of the scattering length with the magnetic field B − B0 for fixed optical field. The solid red line is for ω 1 = ω e1 and ω 2 = ω e2, the dotted black line is for ω 1 − ω e1 = − 5γ e and ω 2 − ω e2 = − 5γ e.

We have demonstrated theoretically that a two-color field can be successfully used to modulate magnetically induced Feshbach resonance in Bose gas. Two-color field coupling the ground state and excited state can change the scattering length and reduce the two-body loss coefficient K₂. The analytical expression of scattering length is derived by solving the Heisenberg equation. The scattering length can be modified by changing the Rabi frequencies or the frequency of the optical field. By choosing the suitable optical parameters, the two-body loss coefficient K₂ can be greatly reduced compared to the usual single optical scheme.