†Corresponding author. E-mail: cyttkl@cuit.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant No. 61402058), the Science and Technology Support Project of Sichuan Province, China (Grant No. 2013GZX0137), the Fund for Young Persons Project of Sichuan Province, China (Grant No. 12ZB017), and the Foundation of Cyberspace Security Key Laboratory of Sichuan Higher Education Institutions, China (Grant No. szjj2014-074).
Higher channel capacity and security are difficult to reach in a noisy channel. The loss of photons and the distortion of the qubit state are caused by noise. To solve these problems, in our study, a hyperentangled Bell state is used to design faithful deterministic secure quantum communication and authentication protocol over collective-rotation and collective-dephasing noisy channel, which doubles the channel capacity compared with using an ordinary Bell state as a carrier; a logical hyperentangled Bell state immune to collective-rotation and collective-dephasing noise is constructed. The secret message is divided into several parts to transmit, however the identity strings of Alice and Bob are reused. Unitary operations are not used.
The principle of quantum mechanics provides the theoretical basis for exchanging information in an unconditionally secure manner. However, channel noise may make information be exchanged in an unsafe way and with low fidelity. A high qubit error rate (QER) caused by channel noise has become an obstacle restricting the further development of quantum communication. The existence of channel noise not only reduces the fidelity of information, but also gives eavesdroppers chances to steal secret information beneath the mask of noise.
In the past two decades, quantum secure communication has developed rapidly. Since Bennett and Brassard[1] proposed the first quantum key distribution (QKD[1– 6]) protocol, another important branch in quantum communication– QSDC[7– 19] has been investigated by many groups. So far, many important protocols have been proposed. In 2002, Long and Liu[7] put forward the first QSDC protocol, in which the secret message is transmitted directly. In 2003, Deng et al.[8] published the famous two-step QSDC protocol (called the two-step protocol). In the two-step protocol, the way of designing the protocol for direct communication of a secret message was given clearly and it was put forward for the first time that QSDC should be performed with a quantum data block. In 2004, the first QSDC based on a sequence of single photons (called the DL04 protocol) was given by Deng and Long.[9] In 2005, the first QSDC protocol based on super-dense coding was developed by Wang et al.[10] In the same year, Wang et al.[11] proposed a QSDC scheme using multi-particle entanglement. In 2007, Li et al.[12] presented a QSDC protocol with quantum encryption. In 2011, the first QSDC protocol based on photonic polarization-spatial hyperentanglement was presented by Wang et al.[13] Meanwhile, many interesting and valuable QSDC schemes with special characteristics were published. Gu et al. put forward a robust QSDC protocol based on a quantum one-time pad over a collective-noise channel[14] and a two-step QSDC scheme with hyperentanglement.[15] Liu et al.[16] proposed a high-capacity QSDC scheme with single photons in both polarization and spatial-mode degrees of freedom. Sun et al.[17] developed a QSDC scheme with two-photon four-qubit cluster states. Ren et al.[18] published a robust QSDC protocol based on the spatial-mode entanglement of a two-photon system. Gu et al.[19] proposed a robust QSDC protocol with spatial quantum states of single photons.
In recent investigations, some researches about quantum secure communication under noisy conditions were reported.[20– 45] These researches focused on the following aspects. (i) How were the effects of noise reduced? Entanglement purification[25, 26, 38, 39, 42] and entanglement concentration[29, 32, 33, 40, 41, 43, 44] were respectively utilized to reduce the effects of noise. (ii) How is the communication immune to noise? The fault tolerant quantum secure communication was implemented by constructing a decoherence-free subspace (which is immune to noise) and transmitting secret information in the subspace.[21, 22, 24, 30, 31, 35] (iii) How is the influence of noise sidestepped? The quantum states were delivered in spatial-mode degrees of freedom or frequency degrees of freedom, which suffers little effect of noise.[34, 36] (iv) How are the errors corrected after communication? Quantum error correction[27, 45] was used to correct error caused by noise. Besides these methods, Li et al.[20] and Deng et al.[28] also proposed self-error-rejecting methods to resist the effect of collective noise. However, to reduce or eliminate the influence of noise, the auxiliary particles were introduced and delivered through the quantum channel, [21, 22, 24, 30– 33, 35, 38] which reduced the channel capacity inevitably. Also in references, [25, 26, 34, 36] only how to reduce or sidestep the influence of noise was considered, no attention was paid to increasing the channel capacity. Therefore, more attention should be paid to the research about high channel capacity quantum secure communication under noisy conditions.
Supper-dense coding is the primary way to increase the channel capacity. Its essential idea is to encode as much information as possible with the minimum number of particles. The principal methods to implement supper-dense coding are to use entanglement states, high-dimensional entanglement states or hyperentanglement states as quantum carriers and combine sublime designing ideas. In most supper-dense coding protocols which are based on entanglement states, the sender encodes secret information on ordinary entanglement states such as Bell states and GHZ states, and the receiver analyzes the Bell states or GHZ states. The receiver decrypts the secret information by distinguishing four Bell states or eight GHZ states. Yet the experiment indicated that in polarization degrees of freedom we cannot completely distinguish Bell states nor GHZ states with linear optical elements.[46] Therefore, the channel capacity cannot achieve theoretical values. Furthermore, although some probabilistic schemes can distinguish Bell states or GHZ states completely, the maximum success chances of these schemes are only 0.5 and 0.25 respectively.[46] Thus, the channel capacity is not increased either. High-dimensional entanglement state is a state in d-dimensional (d > 2) Hilbert space, which can increase the channel capacity greatly, because one high-dimensional particle can carry more than one bit of classical information. For example, the highest channel capacity of supper-dense coding protocol based on d-dimensional (d > 2) Bell states can reach log2d2.[10] However, because high-dimensional entanglement states are difficult to prepare and measure, supper-dense coding protocols based on high-dimensional[10] entanglement states are more difficult to implement.
Hyperentanglement[46– 62] is a state that is simultaneously entangled in multiple degrees of freedom. One hyperentanglement particle can also carry more than one bit of classical information. Compared with high-dimensional entanglement, hyperentanglement is easy to prepare and measure; [50] based on hyperentanglement, the receiver can easily distinguish all Bell states and GHZ states completely. In 2003, Walborn et al.[47] proposed a protocol based on momentum and polarization degrees of freedom, which distinguishes four Bell states completely. In 2007, the conclusion was verified experimentally.[48] In 2011, Wang et al. put forward a supper-dense coding protocol based on hyperentanglement, and the channel capacity achieved four bits of classical information per particle.[50] Recently, also other scholars were involved in the preparation and analysis of hyperentanglement in multiple degrees of freedom, [47– 49, 52, 55– 57] quantum communication protocols based on hyperentanglement[50, 51] and quantum information processing.[49, 53, 54, 58– 62] Sheng et al.[49] discussed the applications in the quantum teleportation of a particle in an unknown state in two different degrees of freedom and in the entanglement swapping of hyperentangled states. In 2012, Ren et al.[53] and Wang et al.[54] studied complete hyperentangled Bell-state analysis for photon systems. Ren et al. studied deterministic photonic spatial-polarization hyper-controlled-not gate assisted by a quantum dot[58] and hyper-parallel photonic quantum computation.[60] Ren et al. proposed a hyperentanglement purification scheme assisted by diamond nitrogen– vacancy (NV) centers inside a photonic crystal cavity[59] and two-step hyperentanglement purification with the quantum-state-joining method.[62] Ren et al.[60] also developed a hyperentanglement concentration scheme for two-photon four-qubit system with linear optics. All these researches laid the foundation for the research of quantum secure communication. However, these supper-dense coding studies are under ideal condition without noise.
In this study, two protocols based on a hyperentanglement state are proposed over a collective-rotation and a collective-dephasing noisy channel respectively. The two protocols are immune to collective-rotation noise and collective-dephasing noise respectively. In the whole process, with hyperentangled Bell state 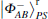
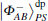
Hyperentanglement is a state that is simultaneously entangled in multiple degrees of freedom. A photon has multiple quantum degrees of freedom. Each degree of freedom can define a qubit under proper conditions. Theoretically, different degrees of freedom can form entanglement, which is called hyperentanglement. For example, a photon with two degrees of freedom can entangle another photon with two degrees of freedom, therefore, a photon can be used as two qubits.
A hyperentangled Bell state in polarization and spatial-mode degrees of freedom can be described as follows:

Here | 0〉 and | 1〉 denote the horizontal and the vertical polarizations of photons respectively. The subscripts A and B represent the two photons in the hyperentangled state, a1 (b1) and a2 (b2) are the different spatial modes for photons A and B. The subscript P denotes the polarization degree of freedom and S is the spatial-mode degree of freedom. A pump pulse of ultraviolet light passes through a beta barium borate (BBO) crystal and produces correlated pairs of photons in the modes a1 and b1. Then it is reflected and traverses the crystal a second time and produces correlated pairs of photons in the modes a2 and b2. Figure 1 is the elementary diagram of hyperentanglement in polarization and spatial-mode degrees of freedom.
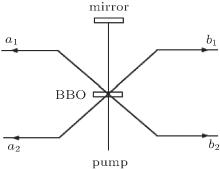 | Fig. 1. Elementary diagram of hyperentanglement in polarization and spatial-mode degrees of freedom. |
For a hyperentangled Bell state in polarization and spatial-mode degrees of freedom, there are 16 Bell states, which can be denoted as

Here | Θ 〉 P denotes one of the following four Bell states in polarization degree of freedom:

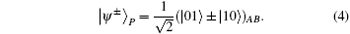
| Ξ 〉 S denotes one of the following four Bell states in spatial-mode degree of freedom:
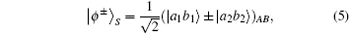
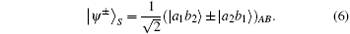
By using CHBSA, [49] 16 hyperentangled Bell states can be distinguished completely. ZP = {| 0〉 , | 1〉 } and

can be selected as two non-orthodox measurement bases in the polarization degree of freedom. ZS = {| a1〉 , | a2〉 } and
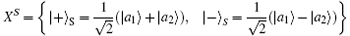
can be selected as two non-orthodox measurement bases in the spatial-mode degree of freedom.
A collective-rotation noise can be described as
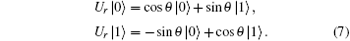
Here θ is the noise parameter, which fluctuates with time. That is, if a | 0〉 state is delivered through channel with collective-rotation noise, the state will change into cosθ | 0〉 + sin θ | 1〉 ; while, a | 1〉 state will change into − sinθ | 0〉 + cosθ | 1〉 . For collective-rotation noise, | ϕ + 〉 and | ψ − 〉 are invariant. Therefore, logical qubits immune to collective-rotation noise are described respectively as
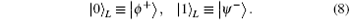
Now let us briefly describe the DSQC protocol based on hyperentanglement against collective-rotation noise. We suppose that the sender, Bob, wants to transmit his secret message to the legitimate receiver, say Alice. Alice and Bob have the secret w-bit string identity (ID) representing their identities. Suppose that Bob’ s secret message is a series of classical 0 or 1 numbers in order, called M.
For a hyperentangled Bell state
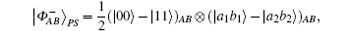
if particle B is delivered through quantum channel with collective- rotation noise, to resist the effect of noise, the sender should represent particle B as a logical quantum state, that is | ϕ + , | 0〉 B should be expressed as | ϕ + 〉 B1B2, and | 1〉 B is expressed as | ψ − 〉 B1B2. Therefore, the logical hyperentangled Bell state should be expressed as
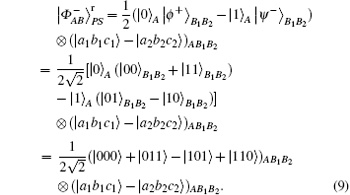
Step 1 Alice prepares N ordered 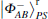
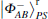
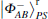
Step 2 Alice inserts the decoy photons ST into sequence SB according to ID, forming a new sequence 

Step 3 After Bob receives 

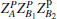
Step 4 Alice and Bob perform S ⊗ S ⊗ S and H ⊗ H ⊗ H operations on particles AB1B2 in turn respectively. Then the combined system of AB1B2 will change into

Here, the phase gate S and Hadamard gate H are represented respectively as
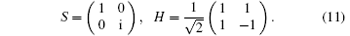
Step 5 Bob publishes the photons that he does not receive in SB, Alice discards the corresponding photons in SA. Therefore, photons in SB will be always one-to-one matching with photons in SA.
Step 6 Alice measures photons in SA with basis ZS = {| a1〉 , | a2〉 } (measurement basis in spatial-mode degree of freedom). Then according to ID, Alice measures photons in SA with basis ZP = {| 0〉 , | 1〉 } or XP = {| + 〉 P, | − 〉 P} (non-orthodox measurement basis in polarization degree of freedom) in order. That is, if the bit of ID is “ 0” , Alice measures the corresponding photon of SA with the ZP basis; otherwise, Alice uses the XP basis. If the measurement result is | 0〉 or | + 〉 , Alice refers to the result as “ 0” ; otherwise, Alice refers to the result as “ 1” . By measuring photons in SA with the basis in spatial-mode and polarization degree of freedom, Alice will obtain the measurement result | a10〉 , | a20〉 , | a11〉 , | a21〉 or | a1+ 〉 , | a2+ 〉 , | a1− 〉 , | a2− 〉 with equal probability. At the same time the states of particles B1B2 are fixed: they are | b1c1〉 | 01〉 , | b2c2〉 | 01〉 , | b1c1〉 | 10〉 , | b2c2〉 | 10〉 or | b1c1〉 | + − 〉 (| − + 〉 ), | b2c2〉 | + − 〉 (| − + 〉 ), | b1c1〉 | + + 〉 (| − − 〉 ), | b2c2〉 | + + 〉 (| − − 〉 ) respectively. And if the measurement result of Alice is | a10〉 , | a20〉 , | a11〉 , | a21〉 , the measurement result of Bob must be | b1c1〉 | 01〉 , | b2c2〉 | 01〉 , | b1c1〉 | 10〉 , | b2c2〉 | 10〉 respectively; and if the measurement result of Alice is | a1+ 〉 , | a2+ 〉 , | a1− 〉 , | a2− 〉 , the measurement result of Bob must be | b1c1〉 | + − 〉 (| − + 〉 ), | b2c2〉 | + − 〉 (| − + 〉 ), | b1c1〉 | + + 〉 (| − − 〉 ), | b2c2〉 | + + 〉 (| − − 〉 ) respectively. If we use binary string {00, 01, 10, 11} to express {| a10〉 , | a20〉 , | a11〉 , | a21〉 }, {| a1+ 〉 , | a2+ 〉 , | a1− 〉 , | a2− 〉 }, {| b1c1〉 | 01〉 , | b2c2〉 | 01〉 , | b1c1〉 | 10〉 , | b2c2〉 | 10〉 } or {| b1c1〉 | + − 〉 (| − + 〉 ), | b2c2〉 | + − 〉 (| − + 〉 ), | b1c1〉 | + + 〉 (| − − 〉 ), | b2c2〉 | + + 〉 (| − − 〉 )}, Alice and Bob will obtain an identical binary string C, which is a real random number.
Step 7 Bob also measures photons B1B2 with the same method as Alice. If the measurement result is | 01〉 , | + − 〉 or | − + 〉 , Bob denotes it as “ 0” ; otherwise as “ 1” . By doing so, Bob will obtain C.
Step 8 Assuming the length of C to be L, Bob divides the secret message M into several parts. Each part is termed Mi (i = 1, 2, … ), which includes the classical secret information about L bits. Bob encrypts the secret message M1 with C bit by bit using XOR operation and obtains C1. That is, C1 = M1 XOR C. Bob publishes C1.
Step 9 Alice decrypts C1 with C bit by bit using XOR operation and obtains M1. That is, M1 = C1 XOR C.
Step 10 Alice stores secret message M1.
Step 11 Alice and Bob begin the next transmission, until all secret messages are finished.
Because the DSQC scheme is designed to be immune to collective-rotation noise, the eavesdropping will be found more easily. Thus, the security of the protocol is mainly guaranteed by the identity string ID (shared by Alice and Bob) and the eavesdropping detection strategy based on 
In the DSQC scheme immune to collective-rotation noise, to reduce the state one needs to prepare the
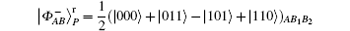
state that is used as decoy photons to detect eavesdropping (that is, only one state is needed). Because the positions of decoy photons are secret, Eve cannot discriminate between decoy photons and information photons (photons in SB).
According to Stingspring dilation theorem, Eve’ s eavesdropping can be implemented by a unitary operation E acting on a bigger Hilbert space HAB1B2 ⊗ HE. The eavesdropping can be represented as

Here, | x〉 E is the initial state of Eve’ s auxiliary particle and | a| 2 + | b| 2 = 1, | m| 2 + | n| 2 = 1. | x0 〉 E, | x1〉 E, | y0〉 E, | y1〉 E are pure states uniquely determined by unitary operation E.
The unitary operation E of Eve can be represented as

The complex numbers a, b, m, n satisfy EE† = I. Therefore, | a| 2 = | m| 2 and | b| 2 = | n| 2 can be obtained.
After Eve’ s eavesdropping, the combined system changes into

After Bob receives 
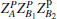
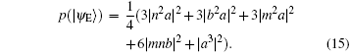
Because | a| 2 = | m| 2 and | b| 2 = | n| 2, then
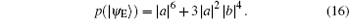
Let | a| 2 = s and | b| 2 = t, then t + s = 1, we can obtain
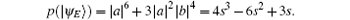
Therefore, the error rate of each qubit is
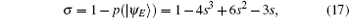
which can also be seen as the lower bound of the detection rate of each qubit eavesdropped:
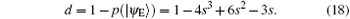
According to the theory of von Neumann entropy, the maximum amount of information contained in qubit | 0〉 is termed

And the maximum amount of information contained in qubit | 1〉 is termed
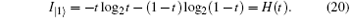
For a qubit transmitting in a quantum channel, it will be in | 0〉 or | 1〉 state with equal probability (p = 0.5); therefore, the total information that Eve can eavesdrop in a qubit will be

According to Eq. (18), we obtain the relationship between s and d as follows:
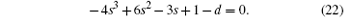
Let

and substitute s into Eq. (22), then we will obtain that

and
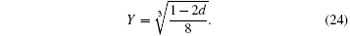
Therefore,
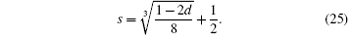
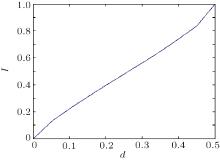
We obtain the relationship between I (the maximum amount of information) and d (the detection rate) as follows:
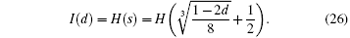
From Fig. 2 we find that when d = 0.5, then I = 1, which is the maximum amount of information Eve can eavesdrop. That is, if Eve performs an attack by using ancillary particles, when she obtains the maximum amount of information on one qubit, the detection rate or qubit error rate reaches 50%.
The ID is shared by Alice and Bob previously. They can share it by executing the QKD protocol; therefore the QKD protocol can guarantee the security of the ID in the process of quantum key distribution. In the process of secret transmission in our protocol, the ID will not be delivered in a classical channel in any form. Therefore, in the process of a secret transmission, the ID will be safe. The only unsafe factor is the improper storage of Alice and Bob. Thus, without considering the unsafe factor of improper storage, the ID can be reused in an unconditionally safe manner.
The original decoy photon idea is proposed by Li et al. in Refs. [63] and [64]. In Refs. [63] and [64], a group of non-orthodox photons are used as decoy photons. In our protocol, the unique qubits
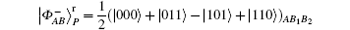
are used as decoy photons. However, the unique qubits 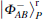

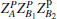
A collective-dephasing noise can be described as

Here ϕ is the noise parameter, which fluctuates with time. That is, if a | 0〉 state is delivered through the channel with collective-dephasing noise, the state will not change; while a | 1〉 state will change into eiϕ | 1〉 . Because two physical qubits with anti-parallel parity obtain the same phase factor iϕ , to defend against collective-dephasing noise, two anti-parallel qubits can form a logical qubit. The logical qubits immune to collective-dephasing noise can be described by Eq. (8), and given as
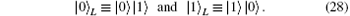
Now we briefly describe the DSQC protocol based on hyperentanglement against a collective-dephasing noise. Suppose that Bob is the sender and Alice is the legitimate receiver. Alice and Bob have the secret w-bit string ID representing their identities. Bob’ s secret message is a series of classical 0 or 1 numbers in order, called M.
For a hyperentangled Bell state
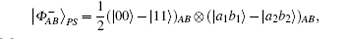
if particle B is delivered through the quantum channel with collective-dephasing noise, to resist the effect of noise, the sender should represent particle B as a logical quantum state, that is, | 0〉 B should be expressed as | 0〉 B1 | 1〉 B2; | 1〉 B is expressed as | 1〉 B1 | 0〉 B2. Therefore, the logical hyperentangled Bell state should be expressed as
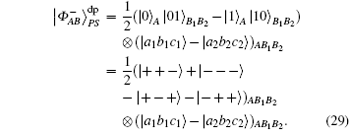
Step 1 Alice prepares N ordered 
Step 2 According to the ID, Alice prepares a qubit sequence ST. As did in Refs. [63] and [64], Alice uses ST as decoy photons. The rule is that she randomly prepares the i-th qubit of ST in | 0〉 or | 1〉 state if the i-th bit of the ID is 0; or else, she randomly prepares the qubit in | + 〉 or | − 〉 state. Alice inserts the decoy sequence ST into the sequence SB according to the ID, forming a new sequence 

Step 3 After Bob receives 

Step 4 Bob publishes the photons that he does not receive in SB, Alice discards the corresponding photons in SA.
Step 5 Alice first measures photons in SA with basis ZS = {| a1〉 , | a2〉 }. Then according to the ID, Alice measures photons in SA with basis ZP = {| 0〉 , | 1〉 } or XP = {| + 〉 P, | − 〉 P}. Like Step 6 in the DSQC scheme against collective-rotation noise, Alice and Bob will obtain an identical binary string C, which is a real random number.
Step 6 The next steps are the same as Steps 7– 11 in the DSQC scheme against collective-rotation noise, which will not be described further here.
Because the DSQC scheme is designed to be immune to collective-dephasing noise, the eavesdropping will be found more easily. Thus, the security of the protocol is mainly guaranteed by the identity string ID (shared by Alice and Bob) and the eavesdropping detection strategy based on | 0〉 , | 1〉 , | + 〉 , and | − 〉 states. Because identity authentication is implemented based on the identity string, the protocol will not be threatened by a man-in-the-middle attack. Next, we analyze the eavesdropping detection rate of the protocol.
In the DSQC scheme immune to collective-dephasing noise, | 0〉 , | 1〉 , | + 〉 , and | − 〉 states are used as decoy photons to detect eavesdropping. Because the positions of decoy photons are secret, Eve cannot discriminate between decoy photons and information photons (photons in SB).
According to Stingspring dilation theorem, Eve’ s eavesdropping can be implemented by a unitary operation E acting on a bigger Hilbert space. The eavesdropping can be represented as
Here | x〉 E is the initial state of Eve’ s auxiliary particle and | a| 2 + | b| 2 = 1, | m| 2 + | n| 2 = 1. | x0〉 E, | x1〉 E, | y0〉 E, | y1〉 E are pure states uniquely determined by unitary operation E.
The unitary operation E of Eve can be represented as
The complex numbers a, b, m, and n satisfy EE† = I. Therefore, | a| 2 = | m| 2 and | b| 2 = | n| 2 can be obtained. The error rate of each qubit is
Let | a| 2 = s, then we will obtain

which can be seen as the detection rate:
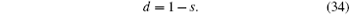
Like that in the collective-rotation noise scheme, the total information that Eve can eavesdrop in a qubit will be
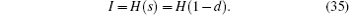
We can calculate that when I = 1, d = 0.5. That is, if Eve performs an attack by using ancillary particles, when she obtains the full information, the detection rate or qubit error rate reaches 50%.
Like that in the collective-rotation noise scheme, the ID is shared by Alice and Bob previously. The only unsafe factor is the improper storage of Alice and Bob. Thus, without considering the unsafe factor of improper storage, the ID can be reused in an unconditionally safe manner. In our protocol, a group of non-orthodox photons (| 0〉 , | 1〉 , | + 〉 , and | − 〉 ) are used as decoy photons, which are nearly the same as the modus operandi of the original decoy photons idea proposed by Li et al. in Refs. [63] and [64]. However, the non-orthodox decoy photons in our protocol are prepared according to the identity string ID, which is secret to others. The special detection strategy implements not only eavesdropping detection in a lure approach, but also identity authentication.
In this study, the two protocols by using hyperentangled Bell state 
(I) Man-in-the-middle attack can be resisted in our protocol.
(II) For two classical bits, only two carrier qubits need to be transmitted once; compared with the two-step protocol, our protocol reduces not only the transmission of carrier qubits but also the number of decoy photons; compared with the protocol based on an ordinary Bell state, in the sense of being immune to collective-rotation noise or collective-dephasing noise, our protocol doubles the channel capacity.
(III) The secret message is divided into several parts to transmit, however the identity string of Alice and Bob is reused.
(IV) Unitary operations are not used.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|
| 51 |
|
| 52 |
|
| 53 |
|
| 54 |
|
| 55 |
|
| 56 |
|
| 57 |
|
| 58 |
|
| 59 |
|
| 60 |
|
| 61 |
|
| 62 |
|
| 63 |
|
| 64 |
|