†Corresponding author. E-mail: gaogan0556@163.com
*Project supported by the National Natural Science Foundation of China (Grant No. 11205115), the Program for Academic Leader Reserve Candidates in Tongling University (Grant No. 2014tlxyxs30), and the 2014-year Program for Excellent Youth Talents in University of Anhui Province, China.
Song [Song D 2004 Phys. Rev. A69 034301] first proposed two key distribution schemes with the symmetry feature. We find that, in the schemes, the private channels which Alice and Bob publicly announce the initial Bell state or the measurement result through are not needed in discovering keys, and Song’s encoding methods do not arrive at the optimization. Here, an optimized encoding method is given so that the efficiencies of Song’s schemes are improved by 7/3 times. Interestingly, this optimized encoding method can be extended to the key distribution scheme composed of generalized Bell states.
As we all know, classical cryptography is conditionally secure because it only relies on the difficulty of solving mathematical problems. However, its counterpart, quantum cryptography, whose security is based on the laws of physics, is unconditionally secure. Due to this merit, quantum cryptography has attracted a lot of attention and produced many promising applications. Quantum key distribution (QKD) is one of these promising applications. The first QKD scheme, [1] in which the quantum states from nonorthogonal bases are used, was proposed by Bennett and Brassard in 1984. Customarily, it is called the BB84 scheme. Subsequently, all kinds of QKD schemes[2– 20] have been put forward. These existing schemes may be divided into three kinds. One is proposed by using only non-entangled states, another by using only entanglement states, and the third by using both. By making use of the statistics, we find that most of the existing QKD schemes have made use of entanglement states. Obviously, entanglement states play an important role in designing QKD schemes. At present, there are several common methods to produce entanglement states, such as nonlinear crystal and optical pulse, [21] ion trap and ions, [22] and cavity QED and atoms, [23] atomic ensembles, [24] and so on. Entanglement swapping[25] is a nice property of quantum entanglement, and also the method where the entanglement among the particles that do not have a direct interaction is produced. For example, consider two EPR pairs in the state 
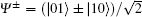


After the Bell measurement on qubits 1 and 3 is performed, the whole system will be in 


In 2004, by using the entanglement swapping of two Bell states, Song[4] first proposed two QKD schemes with the symmetry feature. The schemes are interesting, but their efficiencies are not high, because the classical information that two parties announce is too much during forming keys. In fact, the main reasons for low efficiencies of Song’ s schemes are that the encoding methods are not optimized. In this paper, we will give an optimized encoding method so that the efficiencies of Song’ s schemes are improved by 7/3 times. Meanwhile, we also research whether this optimized encoding method is fit for the QKD scheme composed of other entanglement states.
In this section, we first review Song’ s two QKD schemes, and then give an optimized encoding method for Song’ s schemes, in other words, we propose a modified Song’ s scheme. Meanwhile, we show that the modified scheme and Song’ s original schemes can stand against the entangle-measure attack. Lastly, we make a comparison for the efficiencies of the modified scheme and Song’ s original schemes.
Let us start with the brief description of Song’ s scheme I.
Step 1 Alice prepares an EPR pair of qubits 1 and 2. It is either in Bell basis (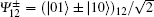

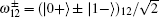
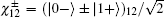
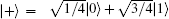
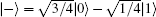
Step 2 Bob prepares an EPR pair of qubits 3 and 4. It is either in 
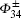


Step 3 Alice sends qubit 2 to Bob, and Bob sends qubit 4 to Alice.
Step 4 Alice and Bob each publicly confirm that the other received the qubits.
Step 5 Alice and Bob also announce which basis is used.
Step 6 If the received qubit was prepared in the rotated basis, Alice (or Bob) rotates back the received qubit into the Bell basis.
Step 7 Alice and Bob perform Bell measurements on 1 and 4, and 2 and 3, respectively.
Step 8 Alice and Bob announce which initial Bell states had been prepared.
Step 9 Knowing the initial Bell states prepared by each other and their own measurement result, they could determine which Bell measurement result the other had got.
Step 10 With the Bell measurement result they got, they share two key bits according to Table 1.
Table 1. “ Id” , “ + − ” , “ Φ Ψ ” , and “ Both” denote four combinations of possible entanglement swapping outcomes.   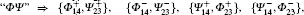  |
Song’ s scheme II is similar to scheme I. The only difference exists in the latter three steps.
Step 8′ Alice and Bob announce the result of their measurements.
Step 9′ Knowing the measurement results for both and their own prepared state, Alice and Bob could determine the initial state prepared by each other.
Step 10′ This enables them to share two key bits according to Table 2.
| Table 2. “ Id", “ + − ", “ Φ Ψ ", and “ Both" denote four combinations of possible prepared states. |
From the above tables, we see that combinations of the measurement results and ones of the initial Bell states are used to discover secret keys in Song’ s scheme I and scheme II, respectively. Obviously, Alice and Bob have to announce their own initial Bell states or their own measurement results of the Bell state in order to form secret keys. By the way, their announcements are finished through a classical channel, moreover, there are a total of three times that classical channels are used in Song’ s schemes. It is used for the first time when Alice and Bob confirm that the transmitted qubits are received and announce which basis is used, and for the second time when announcing the initial Bell states or the measurement results, and for the third time when taking out a sample to check eavesdropping. Hereinto, the quantity of the transmitted information in the second time is the most. In general, classical channels are used as little as possible when designing a quantum communication scheme, which can achieve two advantages, one is to save a communication source, and the other is to debase the threat that the schemes are attacked. Next, by greatly reducing classical channels in Song’ s schemes, we propose a modified scheme, in which a novel encoding method is given. The modified scheme is simply described as follows. The former seven steps are the same as that in Song’ s schemes. The eighth step of the modified scheme may be written as: Step 8 Now Alice and Bob know their own measurement results and initial Bell states. According to Table 3, they can share two key bits.
Now, let us give an explanation for Table 3. Please see the first lattice. Alice’ s or Bob’ s initial Bell states and the possible entanglement swapping results are one of (Φ + , Φ + ), (Φ − , Φ − ), (Ψ + , Ψ + ), and (Ψ − , Ψ − ). There are sixteen combinations, which correspond to the classical bits, “ 00” . In the second lattice, they are one of (Φ + , Φ − ), (Φ − , Φ + ), (Ψ + , Ψ − ), and (Ψ − , Ψ + ). There are also sixteen combinations, which correspond to the classical bits, “ 01” . For the remaining lattices in Table 3, the analysis is similar.
| Table 3. In the bracket (• ), the subscripts 12 and 14 states are Alice’ s initial Bell states and her entanglement swapping results (measurement results), respectively, and the subscripts 34 and 23 states are Bob’ s initial Bell states and his entanglement swapping results (measurement results), respectively. The bracket [• ] denotes one possible entanglement swapping case. |
Clearly, the modified scheme is much simpler than Song’ s schemes. First, its steps are fewer, only eight. Secondly, the requirements that the measurement results or the initial Bell states are announced do not exist, which makes this modified scheme have a high efficiency. In the following, let us calculate its efficiency by employing Cabello’ s efficiency definition[26]

Here, η denotes the efficiency; bs is the expected secret bits received, while qt and bt are the qubit used and the classical bits exchanged between Alice and Bob, respectively. Obviously, in the modified scheme, bs equals 2 bits, and qt and bt equal 2 and 1 bits, respectively. So the efficiency of the modified scheme η equals 2/3. However, the efficiency of Song’ s scheme η only equals 2/7 since its bt equals 5 bits. As a matter of fact, the main reason that the efficiency of the modified scheme is higher than Song’ s is that, the encoding method in the former is more ingenious than those in the latter. By the way, in essence, our encoding method is slightly similar to that in Ref. [9].
Notice that the modified scheme as well as Song’ s schemes need a process to check eavesdropping. Also by taking out a sample and announcing both the correlated measurement results and the initial states, they can judge whether eavesdropping exists. In addition, we see that, in Ref. [4], Song only listed the intercept-resend attack in order to demonstrate that the process is efficient. Obviously, this is not enough. In what follows, we will show that the process is also efficient for standing against the entangle-measure attack.
In advance, an eavesdropper (Eve) prepares an auxiliary qubit that is in | ε 〉 . When qubit 2 is traveling from Alice to Bob, Eve intercepts it, and then performs a unitary operation UE on it and the auxiliary qubit. Without loss of generality, the system state of qubits 1, 2, and the auxiliary qubit can be written as:
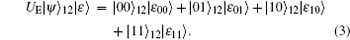
Here, ψ ∈ {Ψ ± , Φ ± }. For qubit 4, what Eve does is the same as that for qubit 2. So the system state of qubits 3, 4, and the auxiliary qubit can be written as:
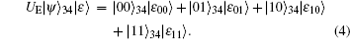
In the modified scheme (and Song’ s schemes), since each EPR pair prepared by Alice and Bob is in Bell basis or rotated basis and there is a process to switch the basis before measuring, this indirectly denotes that two sets of bases are used in checking eavesdropping. When Alice and Bob choose the Bell basis as the measurement basis, in order to avoid introducing error, the following equation must be satisfied
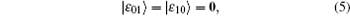
where 0 denotes a null vector. That is, the system states are:
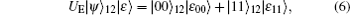
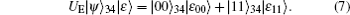
On the other hand, when Alice and Bob choose a rotated basis as the measurement basis, the following constraint can be similarly deduced

Thus, UE| ψ 〉 | ε 〉 = | ψ 〉 ⊗ | ε 〉 , that is, UE| ψ 〉 | ε 〉 is a product of a Bell state and a single qubit. This implies that Eve cannot gain any useful information from observing the auxiliary qubit. In other words, if Eve wants to eavesdrop secret keys by using this attack, his action must introduce errors. Therefore, the processes to check eavesdropping in the modified scheme and Song’ s schemes are also efficient for standing against the entangle-measure attack.
Next, we will investigate whether the encoding method may be extended to QKD schemes composed of other entanglement states. Along the qubit number, we find that the encoding method cannot be used to the QKD scheme composed of any three-qubit entanglement state. However, in four-qubit entanglement states, it seems that it also adapts to the QKD scheme composed of G states.[27] In the following, we will concretely demonstrate this.
(I) Alice prepares qubits 1, 2, 3, 4 either in the generalized Bell basis {| g1〉 , | g2〉 , ..., | g16〉 } (here, | gn〉 = UiUj| g1〉 , | g1〉 = (| 0000〉 + | 0101〉 + | 1010〉 + | 1111〉 )/2, n = 1, ..., 16 and Ui, Uj∈ {I, σ x, σ y, σ z}), or in the rotated basis {| ρ 1〉 , | ρ 2〉 , ..., | ρ 16〉 } (here, 
(II) Bob also prepares qubits 5, 6, 7, 8 either in the generalized Bell basis, or in the rotated basis, which is known only to Bob.
(III) Alice sends qubits 3, 4 to Bob, and Bob sends qubits 5, 6 to Alice.
(IV) Alice and Bob publicly confirm that the two qubits of the other side have been received by each other.
(V) Alice and Bob also announce which bases are used in preparing the four-qubit entangled state.
(VI) If the received qubits were prepared in the rotated basis, Alice (or Bob) rotates back them into the generalized Bell basis.
(VII) They perform generalized Bell basis measurements on qubits 1, 2, 5, 6, and qubits 3, 4, 7, 8, respectively. Obviously, there is an entanglement swapping process. Suppose that Alice’ s qubits 1, 2, 3, 4 and Bob’ s qubits 5, 6, 7, 8 are in | g10〉 and | g1〉 , respectively, and the whole system evolves as follows:

(VIII) Since Alice and Bob know their own measurement result and their own initial generalized Bell state, according to Table 4, they can share four key bits.
| Table 4. The subscripts 1234 and 1256 states are Alice’ s preparing states and her measurement results, respectively, and the subscripts 5678 and 3478 states are Bob’ s preparing states and his measurement results, respectively. The content in the bracket shows one possible entanglement swapping case. |
In each lattice of Table 4, the 16 × 16 entanglement swapping cases correspond to a four-bit key. Here, the so-called “ entanglement swapping case" may be explained as follows. For example, [(| g1〉 1234, | g1〉 1256), (| g1〉 5678, | g1〉 3478)] belongs to one entanglement swapping case. In it, | g1〉 1234 and | g1〉 5678 are initially prepared with G states, and | g1〉 1256 and | g1〉 3478 are one possible measurement result after swapping the entanglement of the G states. In addition, since the number 16 × 16 is too big, here only four indicative cases are listed and others are replaced with suspension points. For clarity, we need further to point out the information that suspension points contain. Let us take the second lattice as an example to explain this. From [(| g3〉 1234, | g1〉 1256), (| g3〉 5678, | g1〉 3478)] to [(| g3〉 1234, | g1〉 1256), (| g14〉 5678, | g16〉 3478)], the array rule of the row is as follows. The contents in all first parentheses, that is, (| g3〉 1234, | g1〉 1256) remain the same, but the ones in all the second parentheses are different. The set of the second states in all the second parentheses is {| g1〉 3478, | g2〉 3478, ..., | g16〉 3478}, and that of the first states is {Iσ z| g1〉 3478, Iσ z| g2〉 3478, ..., Iσ z| g16〉 3478}. Obviously, the set of the first states can be produced based on the set of the second states. From [(| g3〉 1234, | g1〉 1256), (| g3〉 5678, | g1〉 3478)] to [(| g14〉 1234, | g16〉 1256), (| g3〉 5678, | g1〉 3478)], the array rule of the column is similar to that of the row, and the only difference is that the contents in all the second parentheses remain the same and the ones in all the first parentheses will regularly change. For other lattices of Table 4, the array rules are similar.
As in Song’ s schemes, for detecting eavesdropping, also Alice and Bob need to take out a sample from the above raw keys in this QKD scheme composed of G states. By the way, the sample is not big as long as it can provide an analysis of the error rate. Then, they publicly announce the measurement results and the initial generalized Bell states about the sample, so that Alice and Bob can judge whether the quantum channel between them is attacked. If the channel is safe, getting rid of the sample, they will establish the final mature keys. In fact, the manners to check eavesdropping in Song’ s QKD schemes and two proposed schemes are essentially the same as that in the BBM92 scheme, [2] that is, two sets of no-orthonormal quantum states (measuring basis) are employed.
In the end, there are two questions that arise. (i) In Step 7, we see that Alice and Bob perform generalized Bell basis measurements on qubits 1, 2, 5, 6, and qubits 3, 4, 7, 8, respectively. In fact, if Bob sends not qubits 5, 6, but qubits 7, 8, to Alice in Step 3, that is, they perform generalized Bell basis measurements on qubits 1, 2, 7, 8, and qubits 3, 4, 5, 6, respectively, the optimized encoding method can also work. At the moment, we cannot help asking that if Alice sends qubits 2, 4 to Bob, and Bob sends qubits 6, 8 to Alice, can it still work? (ii) Except four-qubit G states, can the optimized encoding method adapt to the QKD schemes composed of other four-qubit entangled states, like, four-qubit GHZ states, [28] four-qubit W states, [29] four-qubit cluster states, [30, 31] four-qubit χ states, [32, 33] etc.? In addition, with the further increase of the qubit number, can the optimized encoding method adapt to the QKD scheme composed of N-qubit (N > 4) entangled states? In our opinion, these questions are interesting and can be studied in the future.
In summary, we have proposed an optimized encoding method for Song’ s QKD schemes, which makes the efficiencies of the schemes improve trebly. The proposed optimized encoding method is not only interesting, but also saves plenty of classical sources for the QKD schemes with the symmetry feature. In other words, our optimized encoding method is economical if it is practically applied. Moreover, we discuss whether the optimized encoding method has more theoretical application. As a result, it is detected that it also adapts to the QKD scheme composed of four-qubit G states. We will continue further research on its application after this work. Finally, let us compare our optimized encoding method with Song’ s encoding methods[4] from a security aspect. Obviously, ours is safer than Song’ s scheme because an eavesdropper needs to guess one result from 4 possible cases if using Song’ s method, but one result from 64 possible cases if using ours.
I thank my parents for their encouragements.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|





