†Corresponding author. E-mail: zhmzc1997@126.com
*Project supported by the Science and Technology Plan of Hunan Province, China (Grant No. 2010FJ3148) and the National Natural Science Foundation of China (Grant No. 11374096).
The population dynamics of a two-atom system, which is in two independent Lorentzian reservoirs or in two independent Ohmic reservoirs respectively, where the reservoirs are at zero temperature or finite temperature, is studied by using the time-convolutionless master-equation method. The influences of the characteristics and temperature of a non-Markovian environment on the population of the excited atoms are analyzed. We find that the population trapping of the excited atoms is related to the characteristics and the temperature of the non-Markovian environment. The results show that, at zero temperature, the two atoms can be effectively trapped in the excited state both in the Lorentzian reservoirs and in the Ohmic reservoirs. At finite temperature, the population of the excited atoms will quickly decay to a nonzero value.
Population trapping arises when a multilevel system interacting with external driving fields is frozen in a given state for a very long time. Population trapping was originally discovered in systems with at least three discrete levels, [1, 2] then was shown to appear in systems with continuum levels[3] and in quantum systems interacting with quantized fields.[4– 6] Its importance is well reflected by its numerous applications in laser cooling, stimulated Raman adiabatic passage, [7, 8] electromagnetically induced transparency, [9, 10] and lasing without inversion.[11] Indeed, population trapping has led to an extensive theoretical and experimental analysis in photonic-bandgap materials interacting with either real atoms[12] or quantum dots.[13, 14]
An analogous phenomenon has been singled out in dynamics of an atom interacting with a structured reservoir. A photon deposited in the cavity may be retained for a very long time though it will eventually be lost in the environment. Consequently, an excited atom with transition frequency detuned from the multi-mode cavity may take a long time to decay but it eventually will dissipate its excitation energy into the environment. In other words, for a two-level atom interacting with a structured reservoir, the atomic population can be partially trapped in the excited state, when the atomic Bohr frequency is near the edge of the gap.[15– 18] This means that, as the time tends to infinity, the atomic population tends to the lower state and the cavity to a state of no excitation.
The population trapping of excited atoms has become of great interest in recent researches of quantum many-body physics, [19] quantum information processing, [20] and quantum nonlinear optics.[21] However, the atomic spontaneous emission and the environment-induced dissipation inevitably lead to decoherence and noise in the quantum system and thus are undesirable in the above quantum physics researches. Recently, non-Markovianities of open quantum systems have been extensively studied[22– 27] and a theoretical approach for treating quantum transport was given in Ref. [28]. The dynamics of two-body systems in different environments have been studied in Refs. [29], [30], and [31]. It is worth pointing out that with the development of the quantum computer, quantum dynamics can be simulated in real time and space and the digital quantum simulation of interacting fermion systems has been realized in experiment.[32]
Thus, for real quantum systems unavoidably interacting with their environments, how to obtain excited population trapping by the feedback and memory effect of the environment has received plenty of attention. In recent years, some schemes[33, 34] have been proposed to study the influence of the non-Markovian effects on the atomic population in the Lorentzian reservoir at zero temperature by the exact solution method. However, it is not only non-Markovian but also nonzero temperature for real environments. In this paper, we investigate the population dynamics of the excited atoms in two independent Lorentzian reservoirs or in two independent Ohmic reservoirs at zero and finite temperature by the time-convolutionless master-equation method. We discuss in detail the influence of the non-Markovian effect, the detuning, and the temperature on the population dynamics. The results show that, at zero temperature, the two atoms can be effectively trapped in the excited state both in Lorentzian reservoirs and in Ohmic reservoirs. At finite temperature, the population of the excited atoms will quickly decay to a nonzero value.
This paper is organized as follows. In Section 2, we present the physical model. Results and discussions are given in Section 3. Finally, a brief summary is given in Section 4.
We consider two two-level atoms, in which each atom couples with a structured reservoir.[35, 36] The Hamiltonian is (ħ = 1)

where
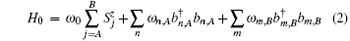
is the free Hamiltonian of the combined system. ω 0 is the transition frequency of the two atoms, 
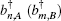
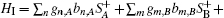
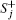
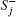

In the second-order approximation, the time-convolutionless (TCL) master equation, [37] described by the density operator ρ AB(t), has the following form
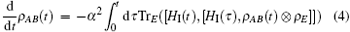
with the environment state ρ E.
Here we have supposed that ρ (t) = ρ AB(t) ⊗ ρ E and TrE([HI(t), ρ AB(0) ⊗ ρ E]) = 0, and equation (4) may be written as
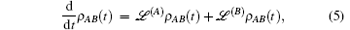
where ℒ (j) (j = A or B) is the Liouville super-operator[34] associated to the Hamiltonian Eq. (3) and it is defined by
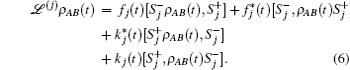
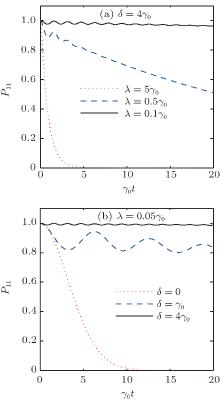
The correlation functions kj(t) and fj(t) are respectively
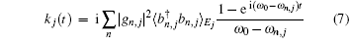
and
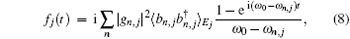
where 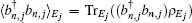

Assuming that the two reservoirs are identical and initially prepared in a thermal state with temperature T, the correlation functions reduce to
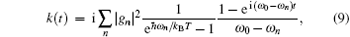
and

here kB is the Boltzmann constant. For a sufficiently large environment, we can replace the sum over the discrete coupling constants with an integral over a continuous distribution of frequencies of the environmental modes, i.e., 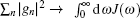
In this section, we investigate the population (P11) of the excited atoms, which is the probability of the system in the state |11〉 , and let the initial state be in the product state |11〉 .
We take a Lorentzian spectral density of reservoir[38]

where δ is the detuning between ω 0 and the center frequency ω of the reservoir. The parameter λ defines the spectral width of the coupling, which is connected to the reservoir correlation time τ R by τ R = λ − 1 and the parameter γ 0 is related to the relaxation time scale τ S by 
Inserting Eq. (11) to Eqs. (9) and (10), we obtain the correlation functions

and
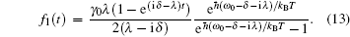
Figures 1(a) and 1(b) present the population dynamics of the excited atoms in Lorentz reservoirs at zero temperature. Figure 1(a) gives the influence of the spectral width λ on the P11 with the detuning (δ = 4γ 0). It can be seen that the behaviors of the P11 have clear differences in both the Markovian and the non-Markovian regimes. When λ = 5γ 0 (i.e., in the Markovian regime), as time goes on, the P11 reduces exponentially and quickly to zero, as shown with the dotted line in Fig. 1(a). When λ = 0.5γ 0 (i.e., with the weak non-Markovian effect), due to the feedback and memory effect of environment, the P11 will oscillate damply and its decay obviously becomes slow, as shown with the dashed line in Fig. 1(a). When λ = 0.1γ 0 (i.e., with the strong non-Markovian effect), the P11 can be effectively trapped for a long time, as shown with the solid line in Fig. 1(a). Therefore the P11 relies on the non-Markovian effect under δ = 4γ 0. Increasing the non-Markovian effect, the P11 can be effectively protected. The time evolution of the P11 for different δ in the non-Markovian regime (λ = 0.05γ 0) is shown in Fig. 1(b). It can be found that the P11 with or without detuning exhibits different behaviors in the non-Markovian regime. When δ = 0 (i.e., without detuning), the P11 also reduces exponentially and quickly to zero, shown as the dotted line in Fig. 1(b). However, when δ = γ 0 (i.e., with small detuning), due to the feedback and memory effect of the environment, the P11 will oscillate damply, as shown with the dashed line in Fig. 1(b). When δ = 4γ 0 (i.e., with large detuning), the P11 can also be effectively preserved for a long time, as shown with the solid line in Fig. 1(b). Therefore, the P11 is obviously dependent on detuning, and the bigger the value of δ is, the more the P11 can be effectively protected.
Therefore, from the above analyses, we find that, only if the detuning and the non-Markovian effect are present simultaneously at zero temperature, can the atomic population be effectively trapped in the excited state for a very long time by increasing the detuning and the non-Markovian effect. The physical interpretation is that, when λ > 2 γ 0 or δ = 0, the quantum information only flows out from the atom and is not returned from its reservoir, so the population dynamics of the excited atoms will reduce exponentially, as shown with the dotted lines in Figs. 1(a) and 1(b). However, when λ < 2 γ 0 and δ ≠ 0, due to the memory and feedback effect of the reservoir, the quantum information flowing to the reservoir will be partly returned to the atom, so the population dynamics of the excited atoms will oscillate damply. And with δ increasing and λ decreasing, the information returned will be more and the atomic decay rate will become smaller, so that the atomic population can be effectively trapped in the excited state for a very long time, as shown with the dashed lines and the solid lines in Figs. 1(a) and 1(b).
 | Fig. 1. Population of the excited atoms as a function of γ 0t in Lorentz reservoirs at zero temperature. The parameter ω 0 = 10γ 0. |
For a given temperature such that kBT/ħ ω 0 = 10, the P11 dynamics is plotted in Figs. 2(a)– 2(d), where figures 2(c) and 2(d) show the very long time behaviors of the P11. Comparing Fig. 1(a) and Fig. 2(a), it can be seen that the influence of temperature on the P11 is clearly visible when δ = 4γ 0. From the dotted lines in Fig. 1(a) and Fig. 2(a), we find that, in the Markovian regime, the difference is in the decay rate of the P11 and in the amount of trapping. The decay of the latter is quicker than that of the former. The amount of trapping in the excited state, in the first case, reaches zero while in the second case it is close to 18%. Comparing the dashed lines and the solid lines in Fig. 1(a) and Fig. 2(a) respectively, we know that, in the non-Markovian regime, the decay rates and the oscillating amplitudes in the second case are larger than those in the first case. From the long time behavior, under zero temperature and the non-Markovian regime, the amount of trapping in the excited state eventually reaches zero (It is not shown in Fig. 1(a)), while it is close to 21% (see the dashed and solid lines in Fig. 2(c)) under kBT/ħ ω 0 = 10 and the non-Markovian regime. Comparing Fig. 1(b) and Fig. 2(b), it can be seen that the influence of temperature on the P11 is also very evident when λ = 0.05γ 0. From the dotted lines in Fig. 1(b) and Fig. 2(b), we find that, without detuning, the difference is also in the decay rate of the P11 and in the amount of trapping. The decay in the second case is quicker than that in the first one. In the first case, the amount of trapping in the excited state reaches zero while it is close to 23% in the second case. Comparing the dashed lines and the solid lines in Fig. 1(b) and Fig. 2(b) respectively, we know that the decay rates and the oscillating amplitudes of the P11 with the detuning are greater than those without the detuning. From the long time behavior, under zero temperature and the detuning, the amount of the P11 eventually reaches zero (it is not shown in Fig. 1(b)), while it is close to 23% (see the dashed and solid lines in Fig. 2(d)) under kBT/ħ ω 0 = 10 and the detuning.
 | Fig. 2. Population of the excited atoms as a function of γ 0t in Lorentz reservoirs at finite temperature kBT/ħ ω 0 = 10. Panels (c) and (d) show very long time behaviors. The parameter ω 0 = 10γ 0. |
Thus, nonzero temperature can accelerate the decay of P11, enlarge the oscillating amplitude of the P11 and increase the amount of trapping in the excited state after a long time, whether in the Markovian regime or in the non-Markovian regime, and whether with detuning or without detuning. The physical explanation is that, at finite temperature, due to the thermal effect of the environment, the influence of environment on the atom becomes large and the atomic dissipation becomes strong so that the oscillating amplitude of the P11 becomes big and the population of the excited atoms decay more quickly. On the other hand, as the mean photon number of the reservoir is not equal to zero, the population of the excited atoms will reduce to a nonzero value after a long time, which is induced by the thermal equilibrium of the total system.
We consider an Ohmic spectral density with a Lorentz– Drude cutoff function[34]
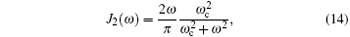
where ω is the frequency of the reservoir, and ω c is the cut-off frequency, which depends on the coupling strength. In this section, we will compare the non-Markovian P11 dynamics with the Markovian one in an Ohmic reservoir in the following three conditions: ω c ≪ ω 0, ω c ≈ ω 0, and ω c ≫ ω 0, where ω 0 is the characteristic frequency of the atom. ω c ≪ ω 0 implies that the spectrum of the reservoir does not completely overlap with the frequency of the atom, that is, the reservoir is effectively adiabatic, so that the dynamical evolution of the system is essentially non-Markovian. While ω c ≫ ω 0 indicates the converse case, which corresponds to the fact that the environmental fluctuations evolve on the shortest possible timescale so that the quantum information is quickly dissipated, the dynamical evolution of the system is Markovian.[42, 43]
Utilizing Eq. (14), the correlation functions in Eqs. (9) and (10) have the following forms
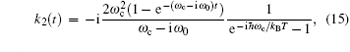
and

Figure 3(a) displays the P11 time evolution of the excited atoms in two independent Ohmic reservoirs at zero temperature. From Fig. 3, it can be observed that the P11 is related to the ratio ω c/ω 0. When ω c/ω 0 = 10 (in the Markovian regime), the P11 reduces quickly to zero, as shown with the dotted line in Fig. 3(a). When ω c/ω 0 = 0.1 (in the non-Markovian regime), the P11 decreases very slowly, as shown with the solid line in Fig. 3(a). Namely, the smaller the value of the ratio ω c/ω 0 is, the stronger the non-Markovian effect is, the more the P11 can be effectively trapped.
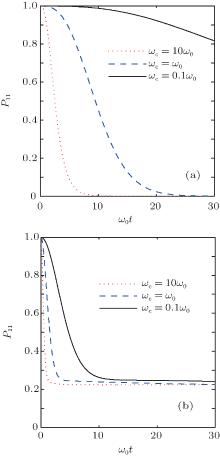 | Fig. 3. In Ohmic reservoirs with a Lorentz– Drude cutoff function, the population of the atomic excited state versus γ 0t for different temperatures. (a) T = 0; (b) kBT/ħ ω 0 = 10. |
Figure 3(b) depicts the P11 time evolution of the excited atoms in two independent Ohmic reservoirs at kBT/ħ ω 0 = 10. Comparing Fig. 3(a) and Fig. 3(b), it can be seen that the P11 is obviously dependent on the temperature. From the dotted lines in Fig. 3(a) and Fig. 3(b), we find that, the decay in the second case is quicker than that in the first one, the amount of the P11 in the first case can reach zero while in the second case it is close to 22%. Comparing the three curves in Fig. 3(b), it is clear that, when the ratio ω c/ω 0 decreases, the amount of population trapping in the excited state increases a little and the decay of the P11 can become slow.
Hence, when the ratio ω c/ω 0 decreases, the atomic decay rate can become small. When the temperature rises, the atomic decay rate can become large and the amount of population trapping in the excited state will increase. The physical mechanism is that, the environmental fluctuations evolve on the shortest possible timescale if ω c ≫ ω 0 so that the quantum information is quickly dissipated, while the reservoir is effectively adiabatic if ω c ≪ ω 0 so that the atomic decay becomes slow. So the decay rate of the P11 will become small with the ratio ω c/ω 0 reducing. At finite temperature, the thermal effect of the environment will accelerate the atomic dissipation so that the decay rate of the population of the excited atoms increases, but the population of the excited atoms will tend to a nonzero value after a time, which is dependent on the thermal equilibrium of the total system.
In the present work, we have investigated the population dynamics of the excited atoms in two independent Lorentzian reservoirs at zero and finite temperatures. The results show that the population trapping of the excited atoms relys on the characteristic and the temperature of the non-Markovian environment. At zero temperature, only if the detuning and the non-Markovian effect are present simultaneously, can the atomic population be effectively trapped in the excited state for a very long time by increasing the detuning and the non-Markovian effect. At kBT/ħ ω 0 = 10, the decay rate and the oscillating amplitude of P11 are greater than those at T = 0, and the amount of trapping in the excited state is about 20% after a long time, whether in the Markovian regime or in the non-Markovian regime, and whether with detuning or without detuning.
We also discussed the population dynamics of the excited atoms in two independent Ohmic reservoirs at zero and finite temperatures. The results show that, at zero temperature, the smaller the ratio ω c/ω 0 is, the more effectively the atomic population can be trapped in the excited state. At kBT/ħ ω 0 = 10, the smaller the ratio ω c/ω 0 is, the faster the decay of the P11 is, and the amount of population trapping in the excited state is a bit bigger than 22% after a long time.
Moreover, our results also show that, the influences of different reservoirs on the population dynamics of the excited atoms are obviously different. For Lorentzian reservoirs, when the detuning and the non-Markovian effect are present simultaneously, due to the memory and feedback effect of reservoirs, the atom can exchange continuously the quantum information with its own reservoir so that the population dynamics of the excited atoms oscillates damply. While, for Ohmic reservoirs, when ω c ≪ ω 0, the reservoir can suppress the decay of the atom so that the population dynamics of the excited atoms always reduces exponentially.
Population trapping in noisy environments is important in many applications, such as quantum many-body physics, quantum information processing, and quantum nonlinear optics. Our results maybe provide references for theoretical and experimental researches on population trapping in noisy environments.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|


