Quantum entanglement plays a fundamental role in quantum information science. Multipartite entanglement provides a critical resource for quantum secret sharing, quantum error-correcting codes and quantum computation.^{[1, 2]} Experimentally, multipartite entanglement has been observed in ion traps, ^[3] photon polarization, ^[4] superconducting phase and circuit qubit systems, ^[5] and nitrogen-vacancy centers in diamond.^[6] All of these experiments center at preparing graph states, including the GHZ states as special cases. A graph state will become a graph diagonal state in a Pauli environment.^{[7, 8]} One of the key issues is to determine whether the GHZ states contaminated by Pauli environment is genuinely entangled or not entangled at all. The action of a general physical decoherece process on an initial density operator ρ can be described by Λ (ρ ), where Λ is a completely positive trace-preserving map. All such maps can be expressed in a Kraus representation, . A very important class of decoherent processes is described by the Pauli maps, separable (non-entangling) maps whose Kraus operators are given by tensor products of Pauli operators X, Y, Z, and the identity. Examples of these are the collective or individual depolarizing, dephasing or bit-flip channels. Hence arbitrary Pauli maps are important noisy channels. Theoretical researches have concentrated on the full separability and biseparability that characterize the entanglement of the GHZ diagonal states.^{[9– 13]} A fully separable state is a probability mixture of product states, thus a fully separable state is not entangled at all in any sense. A biseparable state is a probability mixture of vectors which are products of single qubit pure states and two-qubit pure states. A state can be biseparable, yet inseparable under bipartitions. The criterion for biseparability^[9] of N-qubit GHZ diagonal states and full separability^{[11, 12, 14]} of three-qubit GHZ diagonal states have recently been proved. For a general N-qubit GHZ diagonal state, a sufficient condition has been given for the coincidence of thresholds for full separability and positive partial transpose (PPT).^[11] So if this sufficient condition is fulfilled, we can use the PPT criterion to detect the full separability of an N-qubit GHZ diagonal state. Apart from the separability, the bipartite entanglement evolution has been investigated for GHZ (or more general, graph) diagonal states in Pauli channels.^{[7, 8]} The entanglement evolution is a topic of intensive interest for different systems.^{[15, 16]}

In this paper, we will study the change of an N-qubit GHZ state or a three-qubit GHZ diagonal state passing through independent parallel Pauli channels. The full separability and biseparability of the resultant GHZ diagonal states are analyzed.

The three-qubit GHZ diagonal states take the form

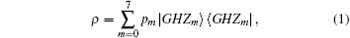
where the p_m form a probability distribution. The GHZ state basis consists of eight vectors

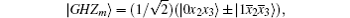
with x_i, x_i ∈ {0, 1} and x_i ≠ x_i. In the binary notation, m = 0x₂x₃ for the “ + ” states and m = 1x₂x₃ for the “ – ” states. Let us consider an 8 × 8 density matrix ρ with entries ρ _ij in the basis | 000〉 , | 001〉 , … , | 111〉 which are ordered in the canonical way. For GHZ diagonal states, the only nonzero elements of ρ are ρ _ii and ρ _{i, 7− i} (i = 0, … , 7), and further we have ρ _ii = ρ _{7− i, 7− i}. More explicitly,

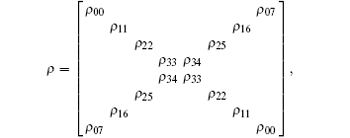
where ρ ₀₀, ρ ₀₇ = (p₀ ± p₇)/2; ρ ₁₁, ρ ₁₆ = (p₁ ± p₆)/2; ρ ₂₂, ρ ₂₅ = (p₂ ± p₅)/2; ρ ₃₃, ρ ₃₄ = (p₃ ± p₄)/2.

Using Pauli matrices X, Y, Z, and 2 × 2 identity matrix I, the GHZ diagonal states can be written as

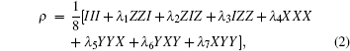
where tensor product symbols are omitted. The parameters λ _i are

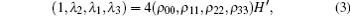
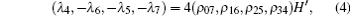
where H′ is a 4 × 4 Hadamard matrix. Denote

then κ = (1 + λ ₋ )/8, with λ ₋ = min{λ ₁ + λ ₂ + λ ₃, λ ₁ – λ ₂ – λ ₃, – λ ₁ + λ ₂ – λ ₃, – λ ₁ – λ ₂ + λ ₃}, and λ ₋ is never positive. So

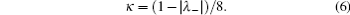
When 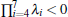, it has already been shown in Ref.  [11] that the positive partial transpose (PPT) criterion is necessary and sufficient for the full separability of a GHZ diagonal state, namely,

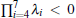
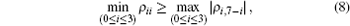
Under the condition we have , thus the condition (7) can be written as

which has a more clear physical meaning that the minimal diagonal element of the density matrix is no less than the maximal absolute value of the off-diagonal element. When the necessary and sufficient criterion for the full separability of a GHZ diagonal state is also known.^[12]

The biseparable criterion for a GHZ diagonal state ρ is^[9]

A graph G = (V, Γ ) is composed of an N vertex set V and an edge set specified by the adjacency matrix Γ , which is an N × N symmetric matrix with vanishing diagonal entries and Γ _ab = 1 if vertices a, b are connected and Γ _ab = 0 otherwise. The neighborhood of a vertex a is denoted by N_a = {v ∈ V| Γ _av = 1}, that is, the set of all the vertices that are connected to a. The graph state related to graph G is defined as

where | μ 〉 is the joint eigenstate of Pauli operators Z_a (a ∈ V) with eigenvalues (− 1)^{μ _a}. It can be shown that the graph state is the joint + 1 eigenstate of the N vertex stabilizers

The N commutative vertex stabilizers are generators of an Abelian group K. The group is called the stabilizer group of the graph state | G〉 . Every element K_s ∈ K stabilizes | G〉 such that K_s | G〉 = | G〉 .

A qubit Pauli channel is described by Kraus operators where f = 1 − p_x − p_y − p_z. The output state of the channel is

for input state ρ . We characterize the channel by a parameter vector (x, y, z) = (p_x, p_y, p_z)/f. Let us consider a local Clifford group which is defined to consist of all local unitary operators mapping the Pauli group to itself under conjugation. There are two basic local Clifford operators, one is the Hadamard gate H, the other is the phase gate P. Up to a global phase factor, any one-qubit Clifford operation is a product of operators chosen from the set {H, P}, where

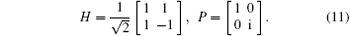
For a single qubit unitary gate U, consider the channel ℰ _U = U^† ○ ℰ ○ U, (here ‘ ○ ’ denotes the successive applications of the gate or channel) we have

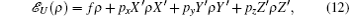
with X′ = U^† XU, Y′ = U^† YU, Z′ = U^† ZU. Hence ℰ _H(ρ ) = fρ + p_xZρ Z + p_yYρ Y + p_zXρ X, for HZH = X. Thus the channel ℰ _H is characterized by the vector (z, y, x). Similarly, for phase gate P, we have ℰ _P(ρ ) with characteristic vector (y, x, z). The local complementary transform is an essential tool in graph state theory. For a graph G and its vertex a, the local complementary operator is

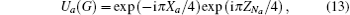
We have ℰ _Ua(ρ _a) with characteristic vector (x, z, y) for qubit a, and ℰ _Ua(ρ _b) (b ∈ N_a) with characteristic vector (y, x, z) for the neighborhood of a.

For two local Clifford equivalent graph states as inputs to parallel Pauli channels, we obtain one output state from another by a proper permutation of the elements of the characteristic vectors. Thus one only needs to study one of the local Clifford equivalent graph states.

For N parallel Pauli channel array with an input of N-qubit graph state | G〉 , we have the output state

with for Pauli error operator , where l_ij = 0, 1, and . The subscript α denotes the index of all possible tensor products of Pauli operators X, Y, Z, and identity I. Consider the output state in graph state bases. A graph state basis is

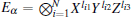
where μ = (μ ₁, μ ₂, … , μ _N) is a binary string, 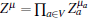. In graph state bases, we have

According to the orthogonality of graph state bases, 〈 G| Z^μ E_α | G〉 = 0 except Z^μ E_α ∈ K up to phase factors ± 1, ± i. Hence

The three-qubit GHZ state is locally equivalent to the graph state | G〉 = H₁H₂| GHZ〉 where H₁ and H₂ are local Haramard transforms on the first and second qubits, respectively. The stabilizer generators are K₁ = X₁Z₃, K₂ = X₂Z₃, K₃ = X₃Z₁Z₂ for the three-qubit graph state. We may list the error operators in Table  1.

Notice that the number of Pauli operators is 4³ for a three-qubit state. The operators in Table  1 exhaust all the 64 Pauli error operators. We classify the error operators in Table  1 according to the stabilizer group K. An error operator E_α may belong to the stabilizer group K or its cosets in the Pauli group. The coset heads are specified by Z^μ . We then get the density matrix of the output state according to Eq.  (17). Consider the parallel Pauli channels with different parameters, namely , with input graph state, the output state is denoted as we have

where (x_i, y_i, z_i) = (p_xi, p_yi, p_zi)/f_i. f_i = 1 − p_xi − p_yi − p_zi are the channel parameters for the i-th qubit. In a more systematical way, 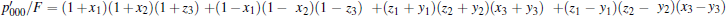, where F = f₁f₂f₃/2.

Table 1.

Table 1.

Table 1. Pauli operators classified as stabilizer group and its cosets. In the table, ‘ St’ stands for ‘ Stabilizers’ , and ‘ Co’ stands for ‘ Cosets’ of the stabilizer group. Co St I K1 K2 K1K2 K3 K1K3 K2K3 K1K2K3 I I X1Z3 X2Z3 X1X2 Z1Z2X3 Y1Z2Y3 Z1Y2Y3 Y1Y2X3 Z1 Z1 Y1Z3 Z1X2Z3 Y1X2 Z2X3 X1Z2Y3 Y2Y3 X1Y2X3 Z2 Z2 X1Z2Z3 Y2Z3 X1Y2 Z1X3 Y1Y3 Z1X2Y3 Y1X2X3 Z1Z2 Z1Z2 Y1Z2Z3 Z1Y2Z3 Y1Y2 X3 X1Y3 X2Y3 X1X2X3 Z3 Z3 X1 X2 X1X2Z3 Z1Z2Y3 Y1Z2X3 Z1Y2X3 Y1Y2Y3 Z1Z3 Z1Z3 Y1 Z1X2 Y1X2Z3 Z2Y3 X1Z2X3 Y2X3 X1Y2Y3 Z2Z3 Z2Z3 X1Z2 Y2 X1Y2Z3 Z1Y3 Y1X3 Z1X2X3 Y1X2Y3 Z1Z2Z3 Z1Z2Z3 Y1Z2 Z1Y2 Y1Y2Z3 Y3 X1X3 X1X2 X1X2Y3

Table 1. Pauli operators classified as stabilizer group and its cosets. In the table, ‘ St’ stands for ‘ Stabilizers’ , and ‘ Co’ stands for ‘ Cosets’ of the stabilizer group.

Consider the channel 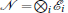with input state | GHZ〉 , the output state is

Denote , then

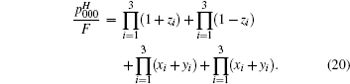
Where we have used the fact that Hadamard transformations on the first and second qubits interchange their channel parameters of bit flipping and phase flipping, namely, x_i ⇔ z_i (i = 1, 2). Denote a_i = f_i + p_zi, b_i = p_xi + p_yi, c_i = f_i − p_zi, d_i = p_xi − p_yi, (i = 1, 2, 3), then

Similarly,

where τ = 1 – τ . Since

for the output state

we have

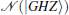
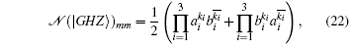
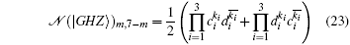
where k_i = 1 – k_i. The entries of the density matrix is

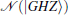
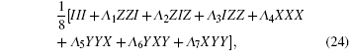
for m = 2k₂ + k₃ ≤ 3. We write the output state in the operator form as

then we have

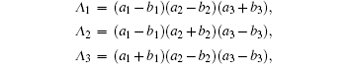
and

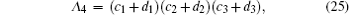
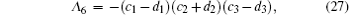
Hence

For any GHZ diagonal state with 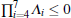, the necessary and sufficient criterion of fully separability is determined by the PPT condition.^{[11, 12]} Thus the fully separability criterion is the PPT criterion for the output state of the GHZ state passing through any parallel Pauli channel.

Consider the separability of a noisy GHZ state. For an initial GHZ state

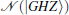
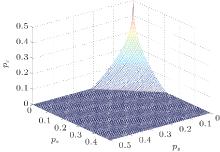
after passing through the parallel Pauli channels the output state is expressed in expression  (24). The fully separable criterion is the PPT criterion  (8), which is

For identical Pauli channels with p_xi = p_x, p_yi = p_y, p_zi = p_z, (i = 1, 2, 3), the fully separable criterion reduces to ab ≥ | c³ + d³| , where a = f + p_z, b = p_x + p_y, c = f − p_z, d = p_x − p_y, and f = 1 − p_x − p_y − p_z. Namely

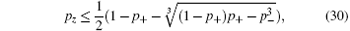
where p_± = p_x ± p_y. The border of the regions of full separability and entanglement is shown in Fig.  1.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. The border surface of full separability and entanglement.

For identical depolarizing channels we have p_x = p_y = p_z = p, the full separable criterion reduces to

The biseparable criterion (9) now reduces to 3ab ≥ | c³ + d³| , namely

The border of the regions of biseparability and genuine entanglement is shown in Fig.  2.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. The border surface of biseparability and genuine entanglement.

For identical depolarizing channels, the biseparable criterion reduces to

Consider the input state of GHZ diagonal state ρ = ∑ _mq_m| GHZ_m〉 〈 GHZ_m| = H₁H₂∑ _mq_m| G_k〉 〈 G_k| H₁H₂, where the binary string m = (m₁, m₂, m₃)∈ {0, 1}³, the binary string k = (m₁ ⊕ m₃, m₂⊕ m₃, m₁). The output state of parallel Pauli channel is

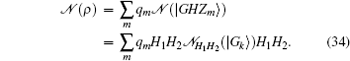
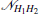
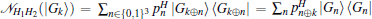
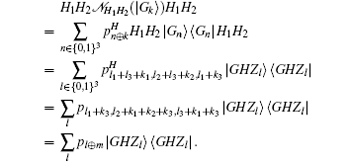
For every input of graph basis state | G_k〉 , the output of channel is . Hence

Thus

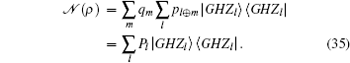
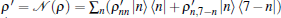
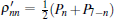
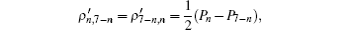
Where P_l = ∑ _mq_mp_{m⊕ l}. In computational basis, we have , with for n = 0, … , 7, and

for n = 0, … , 3. Define

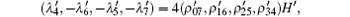
then

Similarly, we have 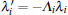for i = 5, 6, 7. Hence we have

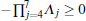
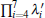
We have proved that for a Pauli channel, thus and have the same sign.

Define 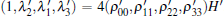, then we have for i = 1, 2, 3. In the operator representation, the output state of the Pauli channel is

for the input state of a GHZ diagonal state  (2), with relationships of

In the operator representation of the input and output states, the effect of the Pauli channel on GHZ diagonal state is simply characterized by the decay of the parameters.

In graph state basis, an N-qubit GHZ state | G〉 is stabilized by the following mutual commutating stabilizer operators

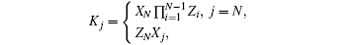
that is, K_j| G〉 = | G〉 , the GHZ state | G〉 is the common eigenstate of all these stabilizer operators K_j with eigenvalues being + 1. Here X_j, Z_j are the Pauli X and Z matrices applied to the j-th qubit. The N-qubit GHZ state is

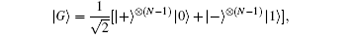
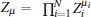
where . All states | G_μ 〉 = Z_μ | G〉 for μ ∈ {0, 1}^{⊗ N} constitute an orthnormal basis set, where . The projector onto the GHZ state has a direct representation in terms of the corresponding stabilizer operators, ^[17]

where . A state ρ = ∑ _μ q_μ | G_μ 〉 〈 G_μ | with q_μ ≥ 0 and ∑ _μ q_μ = 1 is called a GHZ diagonal state, we have

in terms of stabilizer operators, where

and μ , ν ∈ {0, 1}^{⊗ N}. Inversely,

Clearly, we have the trace of the state to be s₀ = ∑ _μ q_μ = 1 and the minimal eigenvalue of ρ should be non-negative, so

Consider the application of the Pauli channel to the initial GHZ state | G〉 . The state will evolve to a mixed state in the form of Eq.  (39) after it passes through the channel. The problem is to determine all the parameters s_μ in Eq.  (39) in terms of the channel parameters. The qubit channel ℰ _i is described by the parameters p_xi, p_yi, p_zi, and f_i = 1 − p_xi − p_yi − p_zi. Denote (x_i, y_i, z_i) = (p_xi, p_yi, p_zi)/f_i as above. We may write in terms of X and Z operators according to the generators of the stabilizer,

For the error operator E_α ∈ K, the input state | G〉 is not changed by the error E_α since K is the stabilizer of | G〉 . The probability of | G〉 after the channel application is the probability of error operator E_α belonging to the stabilizer K. We have

where 0 = (0, … , 0) is the binary string with all elements nullified. We should summarize the corresponding η _α for E_α ∈ K. For the stabilizer operator K_μ with μ _N = 0, the contribution to the probability q₀ is , namely,

where . For the stabilizer operator K_μ with μ _N = 1, the contribution to the probability q₀ is

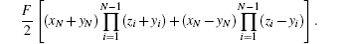
In general, the probability q_μ of obtaining the state | G_μ 〉 when sending the N-qubit GHZ state | G〉 through a parallel Pauli channel is

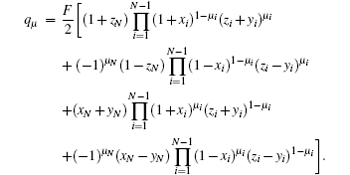
After some algebra, and denoting

we have s_μ for μ _N = 0 and μ _N = 1,

respectively, where a_N, c_N = f_N ± p_zN; b_N, d_N = p_xN ± p_yN; a_i, c_i = f_i ± p_xi; b_i, d_i = p_zi ± p_yi, (i = 1, … , N − 1).

The sufficient condition for the coincidence of the full separability and the PPT criterion of the GHZ diagonal state ρ is that there is δ ∈ {0, 1}^{⊗ (N− 1)} such that ∀ ξ ∈ {0, 1}^{⊗ (N− 1)}, ^[11]

We will prove that inequality  (41) is true for the N-qubit GHZ diagonal state ρ obtained by passing N-qubit GHZ state | G〉 through the parallel Pauli channel. When ξ = 0· · · 0, the left side of inequality  (41) is sign(s_{0· · · 01})s_{0· · · 01}, which is no less than 0. For any ξ with weight 1 (the number of 1 in the N − 1 bit string), say ξ _i = 1 and all the other bits are 0, it is always possible to choose δ _i such that

where s(i) = s_{0· · · 010· · · 01}, the subscript is an N-bit string with i-th bit and N-th bit being 1 and all the other bits being 0.

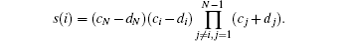
For ξ = 1· · · 10· · · 0, the weight of ξ is i, the first i bits are 1, the rest bits are 0. When i is odd, we have

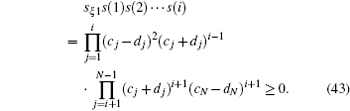
Then

using inequality  (42), we arrive at

When i is even, we have

We also arrive at expression  (44) by using inequalities  (42) and (45).

By interchanging the qubits, we can prove inequality  (41) for any string ξ of weight i and length N − 1. By varying i from 2 to N – 1, the inequality (41) can be proved. Hence the fully separable condition for an N-qubit GHZ state damped by Pauli noise coincides with the PPT criterion. The fully separable condition is^[11] (which can also be obtained from the PPT criterion by choosing the proper bipartition)

For an identical depolarizing channel, p_xi = p_yi = p_zi = p, the condition  (46) is reduced to

for even N, and

for odd N.

The evolution of an N-qubit GHZ state in the Pauli environment is studied. For a three-qubit GHZ state, the Pauli noise contaminated GHZ state is a genuine-entangled state when the Pauli noise is weak (the noise parameter p < 0.071149 for depolarizing channel). It becomes biseparable when the Pauli noise is strong (0.110827 > p ≥ 0.071149 for depolarizing channel). It becomes fully separable when the Pauli noise is more strong (p ≥ 0.110827 for depolarizing channel). The full separability criterion of a Pauli noisy three-qubit GHZ state is proved to be equivalent to PPT criterion. It is determined by comparing the minimum diagonal element with the maximal anti-diagonal element of the density matrix in computational basis. We have also proved that the equivalence of the full separability criterion and PPT criterion for an N-qubit GHZ state contaminated by any parallel Pauli noise. The condition for full separability of a Pauli noisy N-qubit GHZ state is obtained.