†Corresponding author. E-mail: john323@163.com
*Project supported by the National Natural Science Foundation of China (Grant No. 51275523) and the Special Research Found for the Doctoral Program of Higher Education, China (Grant No. 20134307110009).
We theoretically investigate the wave–particle duality based on a Raman atom interferometer, via the interaction between the atom and Raman laser, which is similar to the optical Mach–Zehnder interferometer. The wave and which-way information are stored in the atomic internal states. For the φ − π − π/2 type of atom interferometer, we find that the visibility ( V) and predictability ( P) still satisfy the duality relation, P2 + V2 ≤ 1.
In the beginning of the 20th century, scientists found that the behavior of matter (and also light) can sometimes be described as particles and sometimes as waves, depending on the experimental situation. In 1928, Niels Bohr introduced the principle of complementarity, which is fundamentally important in quantum mechanics.[1] The complementarity expresses that every quantum system has two properties, which are equally real but mutually exclusive, [2– 5] such as wave– particle duality. One observation of the two complementary properties will preclude the simultaneous observation of the other. A typical discussion on the complementarity was Young’ s double-slit experiment with a light beam.[6] In 1979, Wootters and Zurek quantified the wave– particle duality, [7] the predictability (P) of the particle passing along the two paths and the visibility (V) of the interference pattern behind the standard Mach– Zehnder interferometer, and an inequality, P2 + V2 ≤ 1, was theoretically derived by Jaeger et al.[8] and Englert, [9] independently. In Ref. [9], another inequality, D2 + V2 ≤ 1, was also investigated, where the distinguishability D represents a posteriori which-way knowledge after the particle has interacted with the which-way detector, and V is the fringe visibility. Here we would emphasize that the definitions of the two inequalities are different, and both the predictability and the distinguishability are well defined in Ref. [9]. The two duality relations have already been confirmed in experiments[10– 14] and even in a Wheeler’ s delayed-choice experiment.[15– 18] High-order wave– particle duality, [19] the duality with an N-dimensional internal degree of freedom, [20] and the duality for the device with losses[21] are also investigated, all of which satisfy the first inequality (P2 + V2 ≤ 1).
Generally, the duality is discussed in a standard optical Mach– Zehnder interferometer. In 1998, Stephan Dü rr et al. studied the fringe visibility and which-way information in an atom interferometer to experimentally prove the relation between the visibility and distinguishability, D2 + V2 = 1, [22– 24] where Bragg reflection of the atom from standing light waves is used to realize the function of the beam splitters of the interferometer, and the microwaves are used to select the suitable eigenvectors for detecting the distinguishability. Due to the extremely high sensitivity and excellent long-term stability of atom interferometer, a great variety of atom interferometers have been demonstrated since 1924, when de Broglie proposed that a massive particle has wave-like properties.[25] In 1950, Ramsey performed the first experimental demonstration of the interference in atoms.[26] Then atomic physics quickly became a hot topic. Carnal and Mlynek carried out a double-slit experiment with a beam of helium atoms, [27] Keith et al. used diffraction gratings to realize the beam-splitters and mirrors in the atom interferometer, [28] and Riehle et al., [29] Kasevich and Chu, [30, 31] demonstrated the atom interferometer using two-photon stimulated Raman transitions, which is proved to be advantageous for high sensitivities. In this paper, based on the Raman atom interferometer, where the Raman pulses can realize the function of the beam splitters and mirrors of the interferometer, we investigate the relation between the visibility and predictability, P2 + V2 ≤ 1.[9] The visibility and predictability can be obtained by detecting the interference fringes and the difference between the probabilities of atoms passing through the two paths, respectively. We will give a brief introduction of the Raman atom interferometer and discuss the duality relation between the visibility and the predictability in Section 2. Some conclusions are drawn from the present study in Section 3.
As the definition of wave– particle duality in Ref. [9], the wavelike and particlelike behaviors can be described by the visibility of the interference fringe pattern and the predictability about the two paths in the interferometer, respectively. The predictability represents the difference between the probabilities that a particle takes one way or the other way of the interferometer. In the Raman atom interferometer which is similar to an optical Mach– Zehnder interferometer, the wave and particle information can be stored in the long-lived internal states. Then we can obtain the wave– particle duality by detecting the atomic populations in different internal states. In the following, we will first make a brief description about the Raman atom interferometer and then analyse the wave– particle duality based on this type of atom interferometer.
The principle of a Raman atom interferometer has been presented in more detail in Refs. [30]– [34], so we only make a brief description about it here. The Raman atom interferometer is based on the two-photon stimulated Raman transitions. Consider an atom with a three-level system, whose energy level diagram is shown in Fig. 1. The states | g〉 and | e〉 are the two hyperfine ground states and state | i〉 is the excited state. Firstly, the atom absorbs a photon with frequency ω 1 and is pumped into the state | i〉 . Then it is stimulated to emit a photon with frequency ω 2. The Δ is the detuning of the laser frequency relative to the transition frequency of the excited state | i〉 , which is large enough to suppress the spontaneous emission. The scheme of a Raman atom interferometer is shown in Fig. 2. After the interaction of the atoms with a Φ -pulse Raman light, the time-evolution coefficients (cg and ce) in states | g〉 and | e〉 becomes

with the transferred matrix M(Φ ),

where t0 is the initial time and ϕ eff is the effective phase of the two lasers. For the free evolution time T, i.e., without Raman lasers, the transferred matrix becomes a unit matrix, M(0). In the atom interferometer which includes three Raman pulses (see Fig. 2), the atoms are split into two paths, i.e., paths A and B, by the first φ -pulse, acting as a beam splitter with an adjustable reflectivity. After a free evolution time T, it is reflected by a π -pulse and finally recombined by a π /2-pulse. The interferometer fringes can be observed at the output and measured through the atomic population probability in either of the two hyperfine levels.
After the atoms pass through the Raman atom interferometer, the interference fringe can be obtained, i.e., the atom possesses the wave-like characteristic. For the quantization of wave information, it can be described by the visibility of the interference fringe pattern after the φ − π − π /2 type of atom interferometer in Fig. 2, with the expression

where p denotes the population probabilities of atoms in state | g〉 or | e〉 . The maximum and minimum values can be obtained by adjusting the effective phase (ϕ eff) of Raman laser.
We assume that the atom is initially in state | g〉 . Then the total evolution matrix of the φ − π − π /2 type of atom interferometer can be written as

with

where ϕ eff, k denotes the effective phase of the k-th Raman pulse. Substituting Eq. (3a) into Eq. (1a), the population probabilities of atoms in | g〉 and | e〉 states can be obtained as
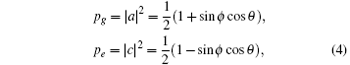
with θ = ϕ eff, 1 − 2ϕ eff, 2 + ϕ eff, 3. By adjusting the effective phase of Raman pulses, we can obtain the maximum and minimum population probabilities of atoms in state | g〉 as

Then the visibility of the interference fringe pattern is

For φ = π /2, we can obtain full wave information (V = 1), while the interference fringe pattern cannot be observed for φ = 0. The same results can be obtained when we detect the population probability of atoms in state | e〉 .
For the which-way information, we remove the second and third pulses in the atom interferometer in Fig. 2. The atoms interact with the first φ -pulse and then are split into two paths. If the internal state of the atom is found to be | g〉 , the atom is transmitted along path A, otherwise it is reflected along path B. So the which-way information can be stored in the atomic internal states and described by the difference between the probabilities (w1 and w2) that atoms passing through paths A and B with an expression as[9]

The probabilities of atoms passing through paths A and B are w1 = cos2(φ /2) and w2 = sin2(φ /2), respectively. For φ = 0, full which-way information is stored, while for φ = π /2, no which-way information is obtained. Then the predictability of the Raman atom interferometer is
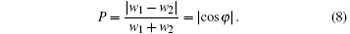
Consequently, equations (6) and (8) indicate that the wave– particle duality relation in a Raman atom interferometer is
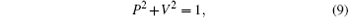
which still satisfies the inequality P2 + V2 ≤ 1. This result demonstrates the quantum-mechanical complementarity of massive particles and illustrates that the wave– particle duality of the atom is in good agreement with the duality relation, P2 + V2 ≤ 1.
In this work, we study the wave– particle duality in a Raman atom interferometer theoretically. The interactions of atoms with π /2-pulse or π -pulse Raman lasers can realize the functions of the 50/50 beam splitter or the mirror in the interferometer, respectively. After the φ − π − π /2 type of atom interferometer, the wave and particle information can be stored in the atomic internal states. By detecting the population probabilities of atoms in the ground states, we finally obtain the duality relation between the visibility and the predictability in the Raman atom interferometer, P2 + V2 = 1, which does not violate the inequality, P2 + V2 ≤ 1.
We thank Huang Jie-Hui for reading the manuscript and his helpful suggestion.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 | [Cited within:1] |
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 | [Cited within:1] |
| 34 | [Cited within:1] |




