Cite this Article
Wang Xiang-Li, Wang Wen-Bo. Harmonic signal extraction from noisy chaotic interferencebased on synchrosqueezed wavelet transform. Chinese Physics B, 24(8): 080203  
Permissions
Harmonic signal extraction from noisy chaotic interferencebased on synchrosqueezed wavelet transform
Wang Xiang-Lia), Wang Wen-Bob)
Wuhan University of Technology, School of Computer Science and Technology, Wuhan 430063, China
School of Science, Wuhan University of Science and Technology, Wuhan 430065, China

†Corresponding author. E-mail: 531448233@qq.com

*Project supported by the National Natural Science Foundation of China (Grant No. 61171075), the Natural Science Foundation of Hubei Province, China (Grant No. 2015CFB424), the State Key Laboratory Foundation of Satellite Ocean Environment Dynamics, China (Grant No. SOED1405), the Hubei Provincial Key Laboratory Foundation of Metallurgical Industry Process System Science, China (Grant No. Z201303).

Abstract

For the harmonic signal extraction from chaotic interference, a harmonic signal extraction method is proposed based on synchrosqueezed wavelet transform (SWT). First, the mixed signal of chaotic signal, harmonic signal, and noise is decomposed into a series of intrinsic mode-type functions by synchrosqueezed wavelet transform (SWT) then the instantaneous frequency of intrinsic mode-type functions is analyzed by using of Hilbert transform, and the harmonic extraction is realized. In experiments of harmonic signal extraction, the Duffing and Lorenz chaotic signals are selected as interference signal, and the mixed signal of chaotic signal and harmonic signal is added by Gauss white noises of different intensities. The experimental results show that when the white noise intensity is in a certain range, the extracting harmonic signals measured by the proposed SWT method have higher precision, the harmonic signal extraction effect is obviously superior to the classical empirical mode decomposition method.

PACS: 02.30.Nw; 31.70.Hq
Keyword: harmonic extraction; noisy chaotic interference; synchrosqueezed wavelet transform
1. Introduction

Many of the signals in nature have chaotic characteristics, such as electrocardiogram (ECG) signal, climate, and sea clutter signal. In addition, the chaotic signal has also been widely used in some professional field, such as chaos secure communication or chaotic electronic countermeasures.[1] In these applications, how to effectively extract the harmonic signal from the mixed signal which is interfered by chaotic signal has very important theoretic and practical significance.[2, 3] Leung et al.[4] estimated the harmonic signal amplitude and frequency in chaotic interference background by the minimum phase space volume method. Haykin and Li[5] studied the small target signal extraction from sea clutter signal with chaotic characteristic by artificial neural network. Stark et al.[6] extracted the harmonic signals of chaotic communication system by chaotic prediction method based on chaotic signal short-term forecasting feature. Wang et al.[7] investigated the harmonic signal extraction from received data contaminated with strong chaotic interference based on the geometry of chaotic interference, the two signals can be successfully separated in the way of projecting chaotic interference and harmonic signals into tangent space and its transverse space of the manifold in which the attractor lies. The above methods can better extract the harmonic signal, but required a more complex condition and a large quantity of calculations.

In recent years, with the development of wavelet and empirical mode decomposition (EMD), [8] the harmonic signal extraction methods from chaotic interference with wavelet or EMD have been widely investigated, and in view of the harmonic signal and chaotic signal they possess different time– frequency characteristics. Wang G G and Wang S X[9] extracted the harmonic signals under chaos interference by using the technology of phase space projection of wavelet transform. Li and Meng[10] used the EMD to decompose the mixed signal composed of harmonic and chaos signal into a series intrinsic mode-type functions (IMFs), and realized the harmonic signal extraction. Wang et al.[11] combined the wavelet and EMD, and proposed a method of extracting the harmonic signal from chaos interference based on the time– frequency characteristics of chaotic signal, noise, and harmonic signal. The EMD is adaptive and more suitable for nonlinear, non-stationary signal decomposition than wavelet. So, the EMD achieves a better effect than wavelet transform in harmonic extraction from chaos interference.

The EMD method can simply and effectively extract the harmonic signal from chaos interference, but the EMD is very sensitive to noise. If the chaos interference signal is added by some noises, the decomposing results of EMD will be seriously affected, resulting in the fact that the harmonic signal cannot be precisely separated.[12, 13] Owing to the effects of equipment and external environment, the noise is inevitable. Therefore how to precisely extract the harmonic signal from chaotic signal contaminated by noise is the problem that must be considered.

The synchrosqueezed wavelet transform (SWT) is a new nonlinear time– frequency reassignment algorithm based on continuous wavelet transform.[14, 15] The SWT can obtain high accuracy time– frequency curve by squeezing the time– frequency map of continuous wavelet transform in the frequency domain. Even if the signal is not basic harmonic signal, the SWT can still accurately calculate its instantaneous frequency.[15] The SWT has better robust to noise. When the signal is contaminated by white noises of different intensities, the SWT can still achieve clearly time– frequency curve and almost invariable decomposition results.[16] The SWT can improve some problems of EMD to some extent, the complex signal contaminated by noise can be accurately separate using SWT.

In this paper, based on SWT, we present a method of extracting harmonic signal from noisy chaotic interference. First, the mixed signal constructed by chaotic signal, harmonic signal, and noise is decomposed into a series of intrinsic mode-type functions (IMTFs), [15] then, the instantaneous frequency of each IMTF is calculated by using the Hilbert transform and according to the instantaneous frequency the needed harmonic signals and the chaotic signal are identified.

In experiments of harmonic signal extraction, the Duffing chaotic signal is selected as interference signal, and the mixed signal of chaotic signal and harmonic signal is added by Gauss white noises of different intensities. The experimental results show that when chaotic interference signals contain the Gauss white noises of different intensities, the extracting harmonic signals measured by the proposed SWT method have higher precision, the harmonic signal extraction effect is obviously superior to the classical empirical mode decomposition method.

2. SWT algorithm

The SWT proposed by Daubechies et al.[15] is a new time– frequency reassigned method based on the continuous wavelet transform. The purpose of SWT is to sharp the signal time– frequency and make the time– frequency curve become finer and clearer, so as to improve the instantaneous frequency precision of the time– frequency curve. The continuous wavelet transform of signal is defined as

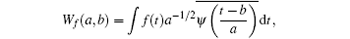
where ψ (x) is the given wavelet function. When Wf (a, b) ≠ 0, the instantaneous frequency of the signal f(t) can be calculated as follows:

Owing to the spread of the wavelet coefficients in the scale direction, [16] the precision of instantaneous frequency curve of non-stationary signal is usually influenced by wavelet transform. The final obtained instantaneous frequency often is not a slender curve, but it is a frequency ribbon.

Assume that the ω l is the l-th central frequency component of the signal f(t), the synchrosqueezed transform is determined only at the center ω l of the successive bins [ω l − Δ ω /2, ω l + Δ ω /2], with Δ ω = ω l − ω l− 1, by summing different contributions:

where ak is the discrete value of the scale a, and Δ ak = ak − ak − 1 . As can be seen from Eq.  (1), SWT will reassign the wavelet coefficient Wf (a, b) ≠ 0 to the (ω l, b) coordinate, and the ω f (a, b) will be limited in the interval [ω l − Δ ω /2, ω l + Δ ω /2]. That means that the instantaneous frequency of each component in f(t) will be squeezed into the narrow interval [ω l − Δ ω /2, ω l + Δ ω /2], and the frequency curve of fk (t) will not present strip, so that the time– frequency maps of non-stationary signal become finer and clearer.

If a continuous function fk (t) = Ak (t)cos (2π ϕ k (t)) satisfies the following properties: Ak (t) ∈ C1(R) ∩ L∞ (R), ϕ k ∈ C2(R), ,

then fk (t) is said to be the intrinsic mode-type function with accuracy ɛ (ɛ − IMT). For the signal

if the fk (t) = Ak (t)cos (2π ϕ k (t)) is a function of intrinsic mode-type function with accuracy ɛ , and satisfies

the f(t) is said to be a superposition of well-separated ɛ -IMTFs with separation d, which is denoted by Aɛ , d. if , the fk (t) can be nearly perfectly reconstructed by summing the SWT coefficients Tf (ω l, b) as

where

the error between reconstructing result and original fk (t) satisfies

whereC is a constant.

3. SWT method of extracting harmonic signal from noisy chaotic interference
3.1. Time– frequency analysis of harmonic signals by SWT in noisy chaotic interference

The SWT method can be successfully applied to the time– frequency analysis of nonlinear, nonstationary signal in noise environment.[15, 16] Assume the harmonic signal in noisy chaotic background to be

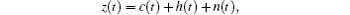
where the 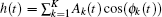denotes the harmonic signal, the c(t) represents the chaotic signal, and the n(t) refers to the Gauss noise, then the harmonic extraction from chaotic interference is identical to the time– frequency analysis of nonlinear, nonstationary noisy environment.

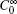
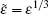
If the harmonic h(t) of the mixed signal is the superposition of ɛ -intrinsic mode-type functions with separation d, that is h ∈ Aɛ , d .[15] Selecting the function g ∈ and ∫ g(t)d t = 1, set , then the M-band synchrosqueezed wavelet transform with accuracy δ and threshold of z(t) can be defined by

where . According to Ref.  [16] we know that the harmonic components of the mixed signal z(t) can be extracted one by one by the M-band synchrosqueezed wavelet transform, and the error between the abstracted harmonic and original harmonic satisfies

where C denotes a constant.

In order to observe the SWT time– frequency ability of the harmonic in noisy chaotic interference signal, by using the Duffing equation to produce the chaotic signal and by adding the harmonic signal and a certain extent of Gauss noise into the chaotic signal, the time– frequency of the mixed signal is analyzed by SWT. The Duffing equation is a nonlinear oscillator with important application background, it has rich dynamic behaviors. Now, these dynamic behaviors have still research important contents. The Duffing equation is expressed as

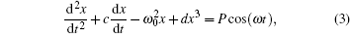
where ω 0 is the natural circular frequency of the system, c is the system damping, d is the nonlinear parameter, P is the excitation amplitude, and ω is the excitation frequency. In this paper, assuming x(0) = 1.0, and using the Runge– Kutta method to numerically solve Eq.  (3). In experiments, the parameters of Duffing equation are assumed to be c = 0.05, , d = 1, ω = 2, P = 10, sampling interval Δ t = π /300, and experimental signal length N = 1.2× 104. The Duffing chaotic signals are denoted as c(t).

In order to investigate the influence of noise for harmonic time– frequency in chaotic background, the noise level (NL) is defined as

where σ n is the standard deviation of noise, σ x is the standard deviation of chaotic signal, and n(t) is the Gauss noise. In the experiment, the two harmonic signals are selected as h1 (t) = sin (120t) + sin (125t), and h2 (t) = sin (120t) + sin (125t) + sin (130t). Setting the NL = 50% of the Gauss white noise n(t), and superimposing the Duffing chaotic signal, harmonic signal, and noise, the two mixed signals are obtained to be z1 (t) = c(t) + h1 (t) + n(t) and z2 (t) = c(t) + h2 (t) + n(t). The SWT time– frequency analysis results of z1 (t) and z2 (t) are shown in Figs.  1(a) and 1(b).

Fig.  1. Analyses of (a) two and (b) three harmonic frequencies versus time based on SWT under chaos interference.

As can be seen from the figure, even the noise level is higher, the SWT can still clearly separate the frequency of chaotic signal from each harmonic signal. Based on the SWT frequency analysis, finding the central frequency of each harmonic and using formula  (2) to reconstruct harmonic, we can realize the harmonic signal extraction under noisy chaos interference.

3.2. Extraction steps of harmonic by SWT from noisy chaotic interference

The extraction of harmonic signal from chaotic interference mainly contains 5 steps as follows.

(i) Calculating the continuous wavelet coefficients of signal. Choosing an appropriate mother wavelet ψ (t), calculating the continuous wavelet coefficient Wz (a, b) of the mixed z(t), and then calculating the instantaneous frequency

(ii) Devising the frequency interval. Assuming the the length of mixed signal f(t) is n = 2L + 1, the sampling time interval is Δ t, setting nv = 32, na = Lnv, Δ ω = [1/na − 1]log 2 (n/2), and ω 0 = 1/nΔ t, and fixing ω l = 2lΔ ω ω 0, l = 0, 1, … , na − 1, then the whole frequency will be divided into different tiny intervals

(iii) Calculating the synchrosqueezed value of the CWT coefficients: setting wavelet coefficients threshold

where , Mk = Wk, then calculating the synchrosqueezed wavelet transform coefficients of z(t) at central frequency ω l, thus

is obtained.

(iv) Extracting each component of the mixed signal. According to Refs.  [13] and [16], calculating each of central frequencies ω q* (k) (k = 1, 2, … , K) of the mixed signal, and setting interval

then extracting each component zk (t) of the mixed signal from formula  (2).

(v) Judging harmonic signal: first, calculating the Hilbert transform of the extracted signal zk (t) and the instantaneous frequency ω k (t) of zk (t). Then using the least square method to fit the instantaneous frequency ω k (t). The chaotic signal is non-stationary and nonlinear signal, so the fluctuation of its instantaneous frequency will become higher over time. The harmonic signal belongs to the linear stationary signal, its instantaneous frequency will tend to be stable over time. So, if the fitting value of ω k (t) approximately equals a constant , the extracted component zk (t) will be considered as a harmonic signal component of the mixed signal.

4. Results and discussion
4.1. Harmonic extraction in Duffing chaotic interference

In the experiment, first, selecting the Duffing signal as the chaos interference, setting the parameters of Duffing equation to be c = 0.05, , d = 1, ω = 2, P = 10, and the sampling interval Δ t = π /300, the first 100 periodic signals are filtered out and the experimental signal length is N = 1.2× 104. Let the mixed signal z(t) = c(t) + h(t) + n(t) composed of the chaotic signal c(t), harmonic h(t), and Gauss noise n(t).

In this paper, we respectively analyze the harmonic abstraction of SWT when the chaotic signal contains a single harmonic and multi harmonic. In experiments, in order to analyze the harmonic extraction ability of SWT method with different noise intensities, we keep the chaotic signal and harmonic unchanged and adjust gradually the Gauss noise intensity. We compare the harmonic extraction precision of SWT with that of the classical EMD method.

4.1.1. Extraction of single harmonic from noisy Duffing chaotic interference

Supposing the mixed signal z(t) = c(t) + h(t) + n(t), where c(t) is Duffing chaotic signal, and h(t) is the harmonic, and n(t) is the Gaussian white noise. The harmonic signal is h(t) = Asin (ω ht), where A = 1.0 and ω h = 0.5. The chaotic signal c(t) is shown in Fig.  2(a), the mixed chaotic signal z(t) of the noise level NL = 40% is shown in Fig.  2(b).

Fig.  2. (a) original chaotic signal, (b) mixed signal composed of chaos, harmonic, and noise, (c) EMD- and (d) SWT-extracted harmonic signal sin(0.5t).

The mixed signal z(t) is decomposed into three intrinsic mode-type functions by EMD, where im f3 (intrinsic mode-type function) is the extracted harmonic component. Comparing im f3 with the input harmonic signal h(t) as shown in Fig.  2(c), the harmonics extracted im f3 by EMD is heavily affected by noise, and there is a large deviation in their frequency and amplitude between im f3 and h(t).

The mixed signal z(t) is decomposed into two intrinsic mode-type functions c1 and c2 by SWT. The frequency analysis indicates that c2 is the harmonic signal extracted from the mixed signal. Figure  2(d) shows the comparison results between the original input harmonic signal h(t) and the decomposed harmonic signal c2 . It can be seen that their frequencies and their amplitudes also roughly keep space except that the amplitudes of the two end portions c3 present a certain attenuation. Figure  2 obviously indicates that the harmonic extraction effect by SWT is better than that by EMD.

When the EMD is used to separate harmonics from the chaotic interference signal with the strong noise, the extraction effect is inevitably affected by noise, and the harmonics cannot be completely extracted. However, SWT method compresses the time– frequency spectrum in the frequency domain direction after wavelet transform. Ever if the chaotic interference signal is polluted by Gaussian white noise, SWT still can obtain highly clear time– frequency curves and there are no cross-terms between time– frequency curves, so SWT has good robustness to noise in the harmonic extraction.

In order to observe the extraction effects of SWT and EMD under different noise intensities, the values of the noise level (NL) are respectively set to be 60%, 80%, 100%, and 120%. Table  1 shows the correlation coefficients (CCs) between the extracted harmonics and the original harmonics respectively by using SWT and EMD. It can be seen that the CC of EMD method is significantly reduced with the increase of the noise level. The CC shows that with the increasing of  the noise strength,   the extraction of harmonic signal becomes more and more difficult  to use the EMD method. When the noise levels are 80% and 100%, the correlation coefficients by EMD method are respectively 0.8628, 0.7517. The CC shows that the extracted harmonic has large distortion. From Table  1, it can be seen that the correlation coefficients of SWT method also decrease with the increase of the noise level. But when the noise level is 120%, the correlation coefficient of SWT is 0.9896, showing that the SWT method still achieves better extraction effect even if the noise level is higher. Based on Figs.  2(c), 2(d) and the experimental results in Table  1, it can be seen that in noisy chaotic interference, the SWT method has a better harmonic extraction effect than the EMD, and in a certain noise strength range, the harmonic signal can be extracted better.

Table 1. The CCs of extracted single harmonic in Duffting chaotic interference.
4.1.2. Extraction of multiple harmonic from noisy Duffing chaotic interference

In order to investigate the multiple harmonic signal extraction ability of the proposed SWT method under the noisy chaotic interference, we set the harmonic signal , where A1 = A2 = A3 = 1.0, , , and , and also set the noise level NL = 40% of the Gauss white noise n(t). Figure  3(a) is the given chaotic signal and the figure  3(b) is the mixed signal z(t) = c(t) + h(t) + n(t).

Fig.  3. Duffing chaotic signal (a); mixed signal composed of chaos, harmonic, and noise (b); EMD-extracted harmonic signal sin(0.5t) (c), sin(0.7t) (d), sin(0.9t) (e); SWT-extracted harmonic signal sin(0.5t) (f), sin(0.7t) (g), and sin(0.9t) (h).

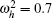
The mixed signal z(t) is decomposed into 7 intrinsic mode-type functions im fi (i = 1, … , 7) by EMD, and through the frequency analysis of Hilbert transform, we know that the im f3, im f4, and im f5 are separated harmonic signals. Figures  3(c)– 3(e) show the comparison results among three original harmonic signals y1, y2, y3 and three extracted signals im f3, im f4, and im f5 . As can be seen from Figs.  3(c)– 3(e), the extracted harmonic signals by EMD are greatly affected by noise, the frequency and amplitude of the extracted signals both have a certain extent of error with respect to the original input harmonic signals.

The mixed signal z(t) is decomposed into 4 intrinsic mode-type functions c1, c2, c3, and c4 by SWT, through the frequency analysis based on Hilbert transform, we know that the c2, c3, and c4 are harmonic signals separated from the mixed signal. Figures  3(f)– 3(h) are the comparison results of the three original harmonic signals y1, y2, y3 and three extracting signals c2, c3, and c4 . As can be seen, the SWT extraction method can better overcome the influences of noise, and the frequency and amplitude of the extracted signal are almost the same as those of the original harmonic signal. As can be seen from Figs.  3(c)– 3(h), when the noise level NL= 40%, the harmonic extraction precision of SWT method is far better than that of EMD method.

The noise level (NL) values are taken to be 40%, 60%, 80%, 100%, and 120% by using the SWT method and EMD method to extract three harmonic signals from noisy chaotic background, and by calculating the CCs between the extracted harmonic signals and original harmonic signals. The CCs are shown in Table  2.

Table 2. The CCs of extracted multiple harmonics in Duffing chaotic interference.

From the data in Table  2, it can be seen that the extracted harmonic signal precision of EMD method is significantly influenced by noise. when the NL= 80%, the correlation coefficients are 0.7367, 0.7418, and 0.6593 between extracted harmonic signal of EMD method and the original harmonic signal. Obviously, the extracted harmonic signals have great distortion, leading to bigger difference from original harmonic signals. From the correlation coefficients of SWT method in Table  2 it can be seen that the SWT method can obtain higher extraction precision for Gauss white noise of different noise levels. Even if the NL= 120%, the correlation coefficients between extracted signal of SWT and original harmonic signal still can reach 0.9272, 0.9250, and 0.9161.The experimental results in Fig.  3 and Table  2 show that under the noisy chaos interference, the multiple harmonic signals extraction method based on SWT has better robust to noise, in a certain noise intensity range, the multiple harmonic signals can be extracted effectively, and the extracted signals have very similarity to original harmonic signals.

4.2. Harmonic extraction in Lorenz chaotic interference

In order to test the harmonic extraction capacity of the proposed method in other chaotic interference, selecting the Lorenz system as the chaotic interference. Lorenz chaotic system model can be described by the following equations:

Set the parameters of Lorenz equation to be c= 10, a= 28, b= 8/3. Let the sampling interval Δ t = π /300, the first 100 periodic signal be filtered out, and the experimental signal length N = 4200. The mixed signal z(t) = c(t) + h(t) + n(t) is composed of the Lorenz chaotic signal c(t), harmonic h(t), and Gauss noise n(t).

Firstly, set the harmonic signal to be h(t) = A sin (ω ht), where A = 1.0 and ω h = 0.5. In order to observe the extraction effects of SWT and EMD under the different noise intensities, the values of the noise level (NL) are respectively set to be 40%, 60%, 80%, 100%, and 120%.

Table  3 shows the correlation coefficients between the extracted harmonics and the original harmonics respectively by using SWT and EMD. It can be seen that when the noise level is more than 80%, the correlation coefficient by EMD method is 0.8795; when the noise level is 120%, the correlation coefficients of SWT can still reach 0.9851. It shows that the SWT method still achieves better extraction effect even if the noise level is higher in Lorenz chaotic interference signal.

Table 3. The CCs of abstracted single harmonic Lorenz chaotic interference.

Secondly, set the harmonic signal to be

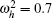
where A1 = A2 = A3 = 1.0, , , and. The mixed signal is z(t) = c(t) + h(t) + n(t), where c(t) is the Lorenz chaotic signal, and n(t) is Gauss noise. The noise level (NL) values are taken to be 40%, 60%, 80%, 100%, and 120%, by using the SWT and EMD method to extract three harmonic signals from noisy Lorenz chaotic background, and by calculating the correlation coefficients (CC) between the extracted harmonic signals and original harmonic signals. The correlation coefficients are shown in Table  4.

Table 4. The CCs of abstracted multiple harmonics in Lorenz chaotic interference.

From the data in Table  4, it can be seen that the extracted harmonic signal precision of EMD method is significantly influenced by noise. when NL= 80%, the correlation coefficients of three abstracted harmonics respectively are 0.7921, 0.7405, 0.7200. Even if NL= 120%, the correlation coefficients of three extracted harmonics by SWT can still reach 0.9702, 0.9534, and 0.9267. Obviously, the precision of abstracted harmonics by the SWT are higher than that of the EMD method.

The experimental results show that under the noisy Lorenz chaos interference, the extracted harmonics by EMD present a bigger difference from the original harmonic signals, and the SWT extracted harmonics method has better robust to noise, the extracted harmonics by SWT are more similar to original harmonic signals.

5. Conclusions

In this paper, the synthesis signal composed of the chaotic signal, harmonic signal, and noise is decomposed into a series of intrinsic mode-type functions based on SWT method, and then the harmonic signals are extracted from the intrinsic mode-type functions by using Hilbert transform. The proposed method is simple and very robust to noise.

In our experiments, the chaotic signal generated by Duffing and Lorenz oscillator is added by the white noises of different intensities, which is selected as the interference signal to shield the harmonic signal. The SWT method and EMD method respectively are used to extract the harmonic signal from the synthesis signal. The comparison of extracting harmonic signal between the SWT and EMD shows that the SWT method can precisely extract the harmonic signal one by one from the noisy chaotic interference signal, and the effect of harmonic signal extraction is better than that of classic EMD method.

Reference
1 Wang W B, Zhang X D and Wang X L 2013 Acta Phys. Sin. 62 050201 DOI:10.7498/aps.62.050201(in Chinese) [Cited within:1]
2 Li X Y, Wang G L and Zhou X X 2014 Chin. Phys. Lett. 31 064204 DOI:10.1088/0256-307X/31/6/064204 [Cited within:1]
3 Hu S L and Shi T Y 2013 Chin. Phys. B 22 013101 DOI:10.1088/1674-1056/22/1/013101 [Cited within:1]
4 Leung H and Huang X P 1995IEEE International Conference ICASSPDetroit: IEEE 1344 [Cited within:1]
5 Haykin S and Li X B 1995 Proc. IEEE 83 94 DOI:10.1109/JPROC.1995.1200273 [Cited within:1]
6 Stark J and Arumugaw B 1992 Int. J. Bifur. Chaos 2 2 DOI:10.1142/S0218127492000409 [Cited within:1]
7 Wang F P, Guo J B, Wang Z J and Xiao D C 2001 Acta Phys. Sin. 50 1019(in Chinese) [Cited within:1]
8 Huang N E, Shen Z, Long S R, Wu M G, Shih H H, Zheng Q, Yen N C, Tung C C and Liu H H 1998 Proc. R. Soc. Lond. A 454 903 DOI:10.1098/rspa.1998.0193 [Cited within:1]
9 Wang G G and Wang S X 2006 Journal of JLN (Jilin) University (Science Edition) 44 439(in Chinese) DOI:10.13413/j.cnki.jdxblxb.2006.03.0272006 [Cited within:1]
10 Li H G and Meng G 2004 Acta Phys. Sin. 53 2069(in Chinese) [Cited within:1]
11 Wang E F, Wang D Q and Ding Q 2011 J. Commun. 32 60(in Chinese) [Cited within:1]
12 Chen G D and Wang Z C 2012 Mechanical Systems and Signal Processing 28 259 DOI:10.1016/j.ymssp.2011.02.002 [Cited within:1]
13 Liu J L, Ren W X and Wang Z C 2013 Journal of Vibration and Shock 32 37(in Chinese) [Cited within:2]
14 Sylvain M, Thomas O and Stephen M 2012 IEEE Trans. Signal Process. 60 5787 DOI:10.1109/TSP.2012.2212891 [Cited within:1]
15 Daubechies I, Lu J F and Wu H T 2011 Applied and Computational Harmonic Analysis 30 243 DOI:10.1016/j.acha.2010.08.002 [Cited within:6]
16 Gaurav T, Eugene B, Neven S F and Wu H T 2012 Signal Processing 93 1079 DOI:10.1016/j.sigpro.2012.11.0292012 [Cited within:5]