†Corresponding author. E-mail: liuxizhong123@163.com
*Project supported by the National Natural Science Foundation of China (Grant Nos. 11347183, 11405110, 11275129, and 11305106) and the Natural Science Foundation of Zhejiang Province of China (Grant Nos. Y7080455 and LQ13A050001).
The nonlocal symmetry of the generalized fifth order KdV equation (FOKdV) is first obtained by using the related Lax pair and then localizing it in a new enlarged system by introducing some new variables. On this basis, new Bäcklund transformation is obtained through Lie’s first theorem. Furthermore, the general form of Lie point symmetry for the enlarged FOKdV system is found and new interaction solutions for the generalized FOKdV equation are explored by using a symmetry reduction method.
In nonlinear science, many effective methods, including Hirota’ s bilinear method, [1, 2] Darboux transformations (DT) and Bä cklund transformations (BT), [3, 4] inverse scattering transformation (IST), [5, 6] symmetry analysis, [7– 14] etc., have been developed to study integrable nonlinear systems. Usually, using these methods one can obtain multiple-soliton solutions and many kinds of nonlinear waves such as conoidal periodic waves, Painlevé waves, and so on. However, interaction solutions between solitons and nonlinear waves are hard to obtain by these traditional methods. Recently, Lou and his colleagues proposed a localization procedure to use nonlocal symmetry for finding interaction solutions and achieved many interesting results.[15, 16]
As we know, using Lie point symmetries of a differential system, one can transform given solutions to new ones via finite transformation and construct group-invariant solutions by similarity reductions. Unfortunately, nonlocal symmetry cannot be used directly to construct exact solutions for nonlinear systems. To conquer that obstacle, one needs to introduce more dependent variables to localize it in a new closed system. In this paper, we use the localization procedure to construct exact solutions for the famous generalized fifth order KdV equation (FOKdV) in the form
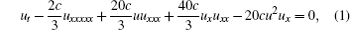
with c as an arbitrary constant. It can be seen that equation (1) generates the usual FOKdV equation when c is taken as 3/2.[17]
It is well known that the KdV equation plays a prominent role in understanding string theory, W-type algebras, statistical mechanics at critical two-dimensional (2D) gravity theories, fluid mechanics, etc. Due to the high nonlinearity of the FOKdV equation, many studies have been carried out on it, including stability properties of the soliton solutions.[18– 20] Especially, the effect of the dispersion due to higher order derivative terms on solitons has been studied for the FOKdV equation which are useful in the context of fluid mechanics and plasma physics.[21, 22] The analytic expressions for the soliton solution to the FOKdV equation have also been found.[23]
The paper is organized as follows. The Lax pair-related nonlocal symmetry of the generalized FOKdV equation is obtained in Section 2 and it is further localized in a new prolonged system by introducing multiple new variables in Section 3. On this basis, the finite group transformation theorem is also found by using Lie’ s first principle. In Section 4, the general form of Lie point symmetry group for the enlarged FOKdV system is obtained and the similarity reduction solutions are explored by using the classical symmetry approach. The last section is devoted to a short summary and discussion.
It is well known that the generalized FOKdV equation possesses the Lax pair

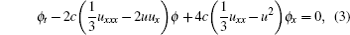
which means that the consistent condition ϕ xt = ϕ tx produces the generalized FOKdV equation (1).
A symmetry σ u of the generalized FOKdV equation is defined as a solution of its linearized equation
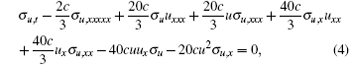
that means equation (1) is form-invariant under the transformation
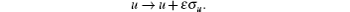
To seek the nonlocal symmetry of the generalized FOKdV equation related with the Lax pair, we use the method proposed in Ref. [24] and write σ u in the form
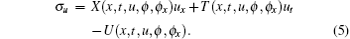
Substituting Eq. (5) into Eq. (4) and eliminating ut, ϕ xx, and ϕ t by Eqs. (1), (2), (3), we obtain the determining equations for the functions X, T, and U. Calculated by computer, the final result is

where di (i = 1, … , 4) are arbitrary constants.
It can be seen from Eq. (6) that not only the Lax pair-related symmetry but also the Lie point symmetry can be obtained by this method.
The nonlocal Lax pair-related symmetry of the generalized FOKdV equation can now be easily obtained by setting d1 = d2 = d4 = 0; the result is
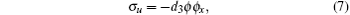
which has also been obtained by using the spectral gradient method.[25, 26]
Apparently, the nonlocal symmetry (7) cannot be used directly to construct explicit solutions for the generalized FOKdV equation. To localize it, we need to introduce new dependent variable
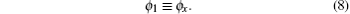
So the system is prolonged and the corresponding symmetry equations are

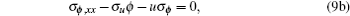
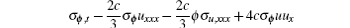

It can be easily verified that a solution of Eq. (9a) has the form


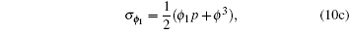
where the new variable p is introduced as
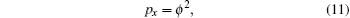
with compatibility condition
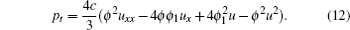
Solving the symmetry equation of Eq. (11)

with Eq. (10a), we get the symmetry for p
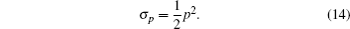
The form of σ p in Eq. (14) indicates that p is a solution of the Schwarzian form of the generalized FOKdV equation
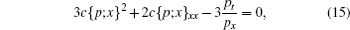
with the Schwarzian derivative
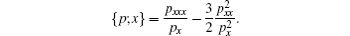
The results (10b) and (14) indicate that the Lax pair-related nonlocal symmetry (7) is successfully localized in the new enlarged system of Eqs. (1), (2), (3), (8), and (11) and the corresponding Lie point symmetry vector takes the form
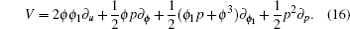
Now, let us study the finite transformation group corresponding to the Lie point symmetry (16), which can be stated in the following theorem.
Theorem 1 If {u, ϕ , ϕ 1, p} is a solution of the prolonged system of Eqs. (1), (2), (3), (8), and (11), then so is 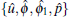
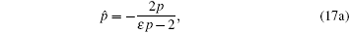

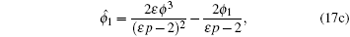
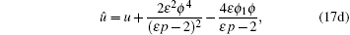
with arbitrary group parameter ɛ .
Proof Using Lie’ s first theorem on vector (16) with the corresponding initial condition as follows:
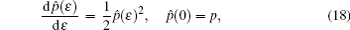
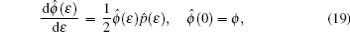
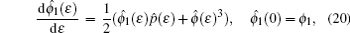
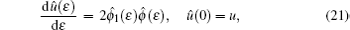
one can easily obtain the solutions of the above equations stated in Theorem 1, thus the theorem is proved.
For the prolonged closed system of Eqs. (1), (2), (3), (8), and (11), we seek the general Lie point symmetry in the form
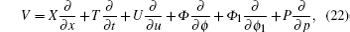
which means that the prolonged system is invariant under the following transformation
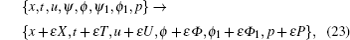
with the infinitesimal parameter ɛ . Equivalently, the symmetry in the form of Eq. (22) can be written as the following function form
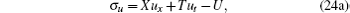
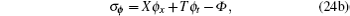
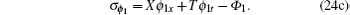
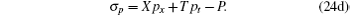
Substituting Eq. (24a) into Eqs. (4), (9b), and (13) and eliminating ut, px, ϕ t, ϕ 1t in terms of the prolonged system, we get more than 100 determining equations for the functions X, T, U, Φ , Φ 1, and P. Calculated by computer algebra, we finally get the desired result
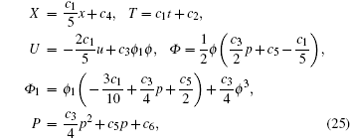
with arbitrary constants c1, c2, c3, c4, c5, c6. When c3 = 2 and c1 = c2 = c4 = c5 = c6 = 0, the obtained symmetry degenerated into the special form in Eqs. (10c) and (14). Consequently, the symmetries in Eq. (25) can be written explicitly as
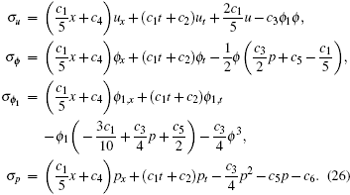
It can be seen from Eq. (26) that the c3-related symmetry is just the Lie point symmetry (10c) and (14) obtained in the last section.
To give the group-invariant solutions of the enlarged system, we have to solve Eq. (26) under symmetry constraints σ u = σ ϕ = σ ϕ 1 = σ p = 0, which is equivalent to solving the corresponding characteristic equation
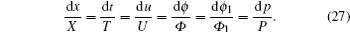
Without loss of generality, we consider the nontrivial symmetry reductions (c3 ≠ 0) in the following two cases:
Case 1ci ≠ 0 (i = 1, 2, 3, 4, 5, 6)
Firstly, we make the transformations c3 → c1c3, c5 → c1c5, c6 → − c1c6 and denote 
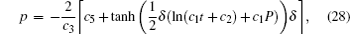
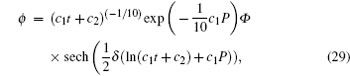
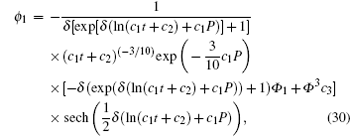
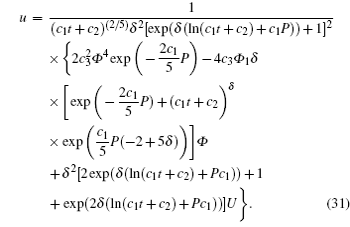
Here, P, Φ , Φ 1, and U are all group-invariant functions with group-invariant variable ξ = (c1x+ 5c4)/(c1t+ c2)15c1.
To get the symmetry reduction equations, we substitute Eqs. (28)– (31) into Eqs. (2), (8), (11), and (15) to find

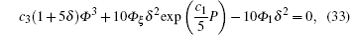
and
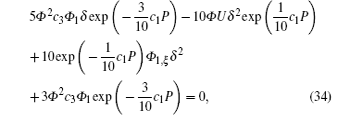
where P satisfied the five-order ordinary differential equation
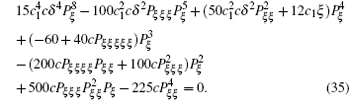
It is clear that when P is solved out from Eq. (35) new group-invariant solutions of the generalized FOKdV Eq. (1) would be immediately obtained through Eq. (31), where Φ , Φ 1, and U can be solved out from Eqs. (32), (33), and (34). The entrance of the tanh part in Eq. (28) indicates that the interaction solution between nonlinear waves and solitons can thus be obtained. This type of interaction solution is hard to obtain by other approaches.
To give out a concrete solution for the generalized FOKdV equation, we derive a simple solution for Eq. (35)
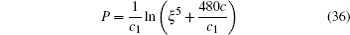
under the constraint condition δ = 1. Then, by solving out Φ , Φ 1, and U through Eqs. (32), (33), (34) and substituting them into Eq. (31), we finally get a rational solution
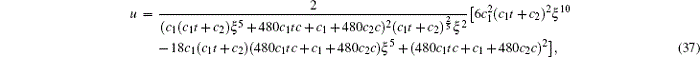
which can be easily verified by substituting Eq. (37) into Eq. (1).
When δ = 0, repeating similar steps those given above, we get explicit solutions for the generalized FOKdV equation as
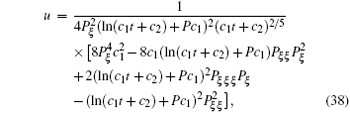
with P satisfying the following equation

Case 2ci ≠ 0 (i = 2, 3, 4, 5, 6) and c1 = 0
In this case, without loss of generality, we make the transformations c6 → − c6 for computing simplicity. When δ ≠ 0, following a similar procedure as in case 1, we obtain the symmetry reduction solutions and the corresponding symmetry reduction equations. Omitting these details, we give the final solution for the generalized FOKdV equation
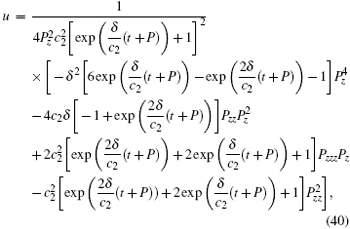
where z = (c2x − tc4)/c2 is the group-invariant variable and the invariant function P satisfies
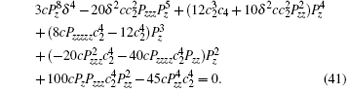
As a simple example, we give the solution of Eq. (41) as
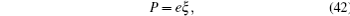
with e as a constant satisfying
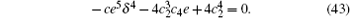
It results in a soliton solution for the generalized FOKdV equation
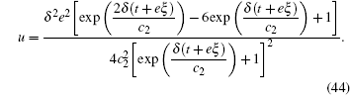
When δ = 0, similar to the above case, we obtain exact solutions for the generalized FOKdV equation, which reads
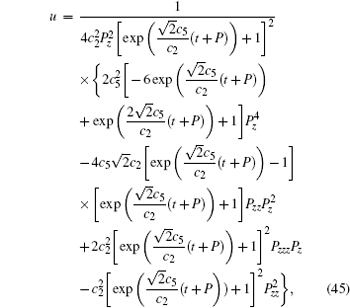
with P satisfying the following reduction equation
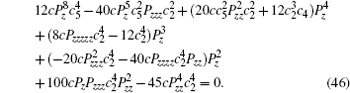
In summary, the Lax pair-related nonlocal symmetry has been obtained and used for deriving new exact solutions for the generalized FOKdV equation. For that purpose, multiple new dependent variables are introduced to localize it in a new enlarged system. On this basis, new Bä cklund transformation is obtained by using Lie’ s first theorem, from which new exact solutions can be derived from trivial seed solutions. Furthermore, the general form of Lie point symmetry for the enlarged generalized FOKdV system, which includes the localized Lax pair-related nonlocal symmetry as a special case, is successfully obtained and the corresponding symmetry reduction solutions are explored. Two cases of symmetry reductions are then obtained, from which new interaction solutions for the generalized FOKdV equation can be obtained.
In this paper, we have shown that nonlocal symmetry can be used for constructing new exact solutions of the generalized FOKdV equation, so it is meaningful to get as many nonlocal symmetries as possible. Besides the method using a Lax pair to derive nonlocal symmetries, there exist some other methods to obtain nonlocal symmetries, such as those obtained from Bä cklund transformation, [27] the bilinear forms and negative hierarchies, the nonlinearizations, [28, 29] and self-consistent sources, [30] etc. Using these various nonlocal symmetries to construct new interaction solutions for integrable systems deserves deeper investigation.
The authors are indebt to the referees and thank them very much for their comments and suggestions.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|


