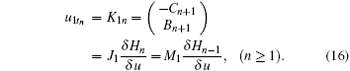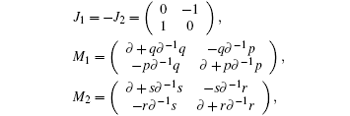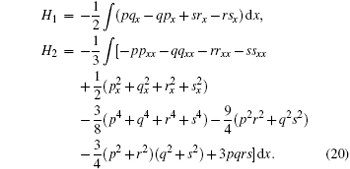 )
)
 )
) †Corresponding author. E-mail: wangelxz@126.com
*Project supported by the National Natural Science Foundation of China (Grant Nos. 61170183 and 11271007), SDUST Research Fund, China (Grant No. 2014TDJH102), the Fund from the Joint Innovative Center for Safe and Effective Mining Technology and Equipment of Coal Resources, Shandong Province, the Promotive Research Fund for Young and Middle-aged Scientisits of Shandong Province, China (Grant No. BS2013DX012), and the Postdoctoral Fund of China (Grant No. 2014M551934).
In this paper, we first introduce a Lie algebra of the special orthogonal group, g = so(4, ), whose elements are 4 × 4 trace-free, skew-symmetric complex matrices. As its application, we obtain a new soliton hierarchy which is reduced to AKNS hierarchy and present its bi-Hamiltonian structure and Liouville integrability. Furthermore, for one of the equations in the resulting hierarchy, we construct a Darboux matrix T depending on the spectral parameter λ.
), whose elements are 4 × 4 trace-free, skew-symmetric complex matrices. As its application, we obtain a new soliton hierarchy which is reduced to AKNS hierarchy and present its bi-Hamiltonian structure and Liouville integrability. Furthermore, for one of the equations in the resulting hierarchy, we construct a Darboux matrix T depending on the spectral parameter λ.
With the development of soliton theory, Lie algebra shows great promise. As it is well known, professor Tu presented a method which used Lie algebra as a tool to construct systematically the Lax equation. Especially, Tu[1] obtained trace identity-based loop algebra A1. Later, many kinds of Lie algebras and their subalgebras were constructed, and some hierarchies with physics meanings are given.[2– 11] Recently, professor Ma[12] generated a hierarchy of soliton equations associated with the real Lie algebra so(3, ℝ ) and shows that each equation has a bi-Hamiltonian structure and integrable in the Liouville sense. The real Lie algebra of the so(3, ℝ ) is not isomorphic to the real Lie algebra sl(2, ℝ ) over the real field ℝ , and the soliton hierarchy[12] is not gauge-equivalent to the famous AKNS soliton hierarchy over the real field ℝ . In fact, the two Lie algebras are isomorphic to each other over the complex field 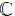
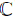
It is known that Darboux transformation provides us with a purely algebraic and powerful method to find a new solution of a nonlinear equation from a known solution in Refs. [13]– [16]. The classical Darboux transformation[17] mainly deals with a Sturm– Liouville problem, which presented solutions to the Korteweg-de Vries hierarchy of (1 + 1)-dimensional integrable systems with new potentials and new wave functions. Based on the work, proper transformation that applies to (2 + 1)-dimensional integrable systems was found. The method of the Darboux transformation has also been applied to the discrete integrable systems successfully. The present paper aims to review application of the Darboux transformation technique for superintegrable systems. In general, we assume every element of T is polynomial with respect to λ .
In this paper, we first introduce a Lie algebra of the special orthogonal group, g = so (4, 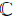
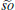
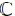
Firstly, let us consider the simple Lie algebra of the special orthogonal group, G = so(4, 


and the structure equations of so(4, 

We point out that the subalgebra G1 = span{e1, e2, e3} of so(4, 
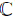
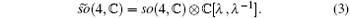
In the following, we work out a new soliton hierarchy from the matrix loop algebra 
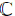
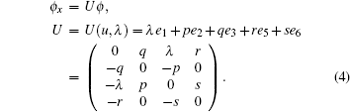
Setting
then the stationary zero curvature equation
gives rise to a solution for V as follows:
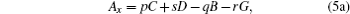
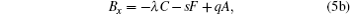
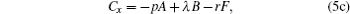


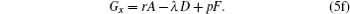
Substituting
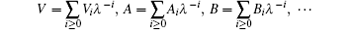
into Eqs. (55), we obtain
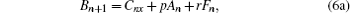


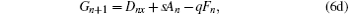

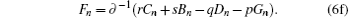
On taking the initial values
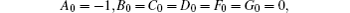
and determining the sequence of {Ai, Bi, Ci, Di, Fi, Gi, | i > 0}. Therefore, the first few sets can be computed as follows:


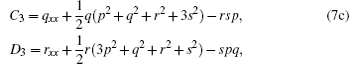
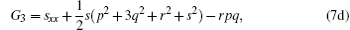
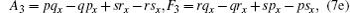
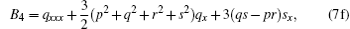
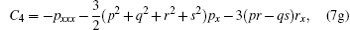
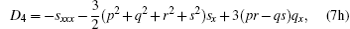

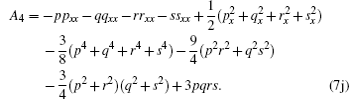
Now, taking

and reading a hierarchy of soliton equations:
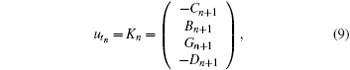
from the zero curvature equations, we have
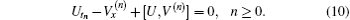
It is direct to compute that
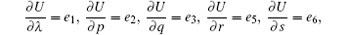
and read

Now the corresponding trace identity becomes
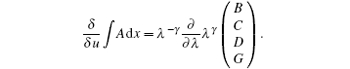
Balancing coefficients of each power of λ in the above equality we obtain

The case of m = 1 tells γ = 0, and thus we have
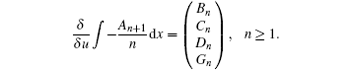
Consequently, we obtain the following Hamiltonian structure for the soliton hierarchy (9)
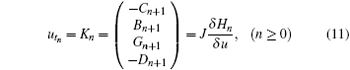
with the Hamiltonian operator

and the Hamiltonian functionals
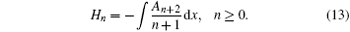
The recursion operator ϕ can be determined by the recursion relations (6a)– (6f)
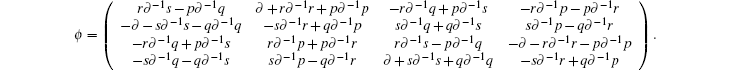
Equation (9) has bi-Hamiltonian structure
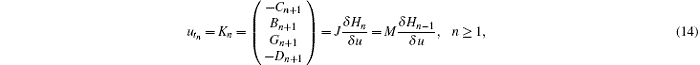
with the Hamiltonian operator
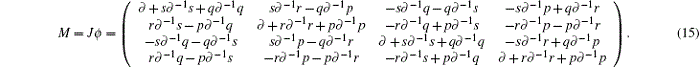
We consider the spectral problem (4) by introducing the temporal part
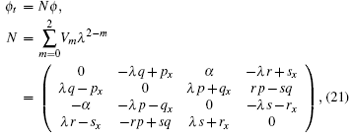
where 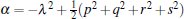
The compatibility condition ϕ xt = ϕ tx yields a zero curvature equation

Now we consider a Darboux transformation
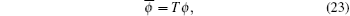
where T is defined by
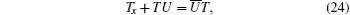
and
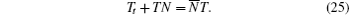
A new spectral problem reads
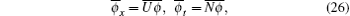
where
Now we consider the basic forms of T. First of all, we assume

where aij and bij (i, j = 1, 2, 3, 4) are functions of x and t. By inserting Eq. (27) into Eq. (24), we read that the coefficients matrix of λ 2 are

In the following, we consider the simplest non-trivial forms of T
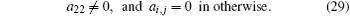
Under the condition equation (29), we insert Eq. (27) into Eq. (24) again, compare the coefficients of λ j (j = 2, 1, 0), and know it is obviously trivial for the case of j = 2. We then have

for the coefficients matrix of λ (j = 1)
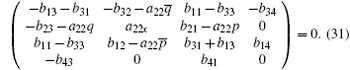
The case of j = 0 leads to the following equations
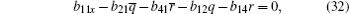
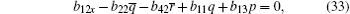
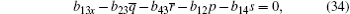
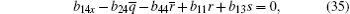

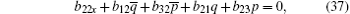
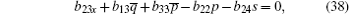
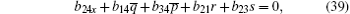
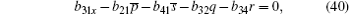
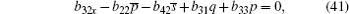
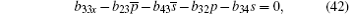

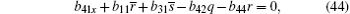
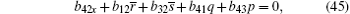
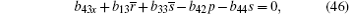
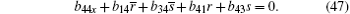
On the other hand, the solutions Φ ,

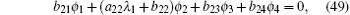
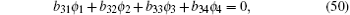
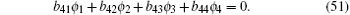
By substituting Eqs. (32), (42), (34), (40), (37), and (47) into Eq. (30), we get
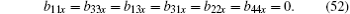
Combining Eq. (30) with Eqs. (48)– (52), we get
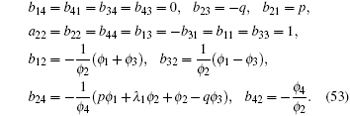
The unknown functions
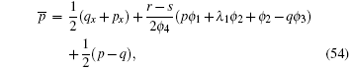
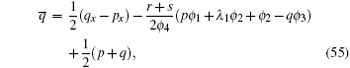
and unknown functions

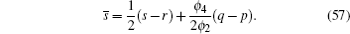
The others of Eqs. (32)– (47) can be proved to be satisfied automatically (under the condition ϕ x = Uϕ ).
If one can prove that the transformation equation (27) maps Eq. (21) into
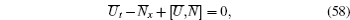
so that (
The main idea of the proof is following: here we only need to prove equation
Let us compare the coefficient of λ j (j = 3, 2, 1, 0). It is trivial for the cases of j = 3. For the case of j = 2, the coefficients matrix is
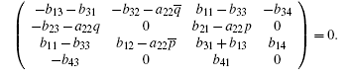
We have the same form as Eq. (31) when a22x= 0.
The case of j = 1 leads to the following equations
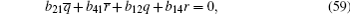
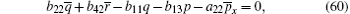
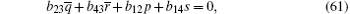
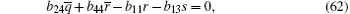

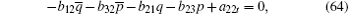
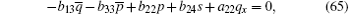

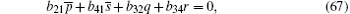
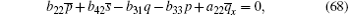

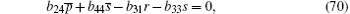
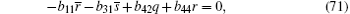



After substituting Eqs. (32)– (38), (40)– (44), (46), (47) into Eqs. (59)– (65), (67)– (71), (73), (74) respectively, and replacing Eqs. (66) and (72) with Eq. (30), then we find equations (59)– (74) are valid.
Also the following equations are presented from the case of j = 0
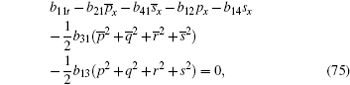
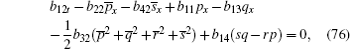
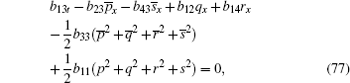
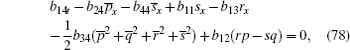
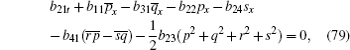
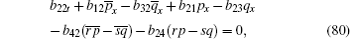
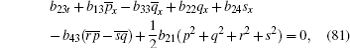
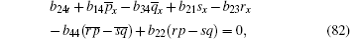



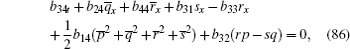
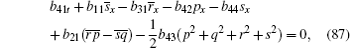

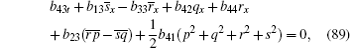
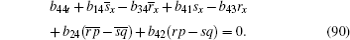
Here, we only give the proof of Eq. (88) for brevity.
From Eq. (53) and ϕ x= Uϕ , we read

Also, from Eqs. (56) and (57), we have
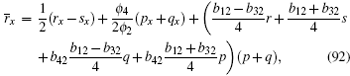
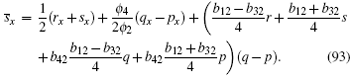
Again, from Eqs. (53) and ϕ t = Nϕ , we propose that
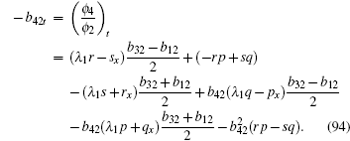
We know that equation (88) is true by substituting Eqs. (53)– (57), (92)– (94) into Eq. (88).
As the subalgebras of so(4, 
In the past, general coupling form[18– 23] by making use of Lie algebra A1, A2 and their subalgebras was presented in the following

and general super-integrable hierarchy form through use of Lie subalgebra B(0, 1) was proposed by Li, [24] Ma[25] as follows:

In this paper, we obtained the integrable coupling by making use of orthogonal Lie algebra so(4, 
Authors would like to thank Professor Ma Wen-Xiu for his useful discussion during his visit to Shandong University of Science and Technology of China.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|