Cite this Article
Lin Dong-Feng, Xu Yu-Zhuan, Shi Jiang-Jian, Zhang Yu, Luo Yan-Hong, Li Dong-Mei†, Meng Qing-Bo‡. Real-time quantitative optical method to study temperature dependence of crack propagation process in colloidal photonic crystal film. Chinese Physics B, 24(7): 077803  
Permissions
Real-time quantitative optical method to study temperature dependence of crack propagation process in colloidal photonic crystal film
Lin Dong-Fenga),b), Xu Yu-Zhuana),b), Shi Jiang-Jiana),b), Zhang Yua),b), Luo Yan-Honga),b), Li Dong-Mei†a),b), Meng Qing-Bo‡a),b)
Key Laboratory for Renewable Energy, Chinese Academy of Sciences, Beijing 100190, China
Beijing Key Laboratory for New Energy Materials and Devices, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China

†Corresponding author. E-mail: dmli@iphy.ac.cn

‡Corresponding author. E-mail: qbmeng@iphy.ac.cn

*Project supported by the National Basic Research Program of China (Grant Nos. 2012CB932903 and 2012CB932904) and the National Natural Science Foundation of China (Grant Nos. 51372270, 11474333, and 21173260).

Abstract

A real-time quantitative optical method to characterize crack propagation in colloidal photonic crystal film (CPCF) is developed based on particle deformation models and previous real-time crack observations. The crack propagation process and temperature dependence of the crack propagation rate in CPCF are investigated. By this method, the crack propagation rate is found to slow down gradually to zero when cracks become more numerous and dense. Meanwhile, with the temperature increasing, the crack propagation rate constant decreases. The negative temperature dependence of the crack propagation rate is due to the increase of van der Waals attraction, which finally results in the decrease of resultant force. The findings provide new insight into the crack propagation process in CPCF.

PACS: 78.67.–n; 62.20.mt
Keyword: colloidal photonic crystal; crack propagation; temperature; real-time quantitative optical method
1. Introduction

Cracks exist commonly in drying colloidal films, [1– 11] clays, [12, 13] and paintings.[14– 16] They not only can influence the rigidity and quality of materials, but also can be applied to identify the age, origin, and art forgery of paintings.[14– 16] Cracking in drying colloidal photonic crystal film (CPCF) is one of representative phenomena and attracts the attention of researchers all over the world.[3, 4, 6, 8– 10, 17] In theoretical studies, efforts are mainly devoted to investigating the mechanism and building models of crack propagation, including stick-slip motion[8] and particle deformation models.[5, 7, 17] Some models based on particle deformation have been set up, suggesting that particle deformation resulting in cracks is caused by different forces, such as surface tension, van der Waals, and tensile stress. However, these models emphasize on the critical time when cracks propagate in the film, while a whole crack propagation process is little investigated.

In experimental studies, efforts are mainly devoted to the final states of crack such as types[1] and spacing.[3, 6] Recently, Routh[6] and Wang[3] found that the final crack spacing increases when the temperature increases[6] or the particle radius decreases.[3] However, crack spacing is not suitable for characterizing cracks when the cracks are not parallel. Because of the lack of a real-time quantitative method for crack measurement, the crack propagation process remains unrevealed. Moreover, further detailed insight into the temperature dependence of the crack propagation rate is still unclear. Thus, real-time quantitative studies on the crack propagation process and the influence of temperature on crack propagation rate are essential for understanding the mechanism of this process.

In our previous work, [18– 20] an experimental method for CCD observation and reflectance measurement of the crack propagation was developed. In the present work, a real-time quantitative optical method is developed to characterize cracking in CPCFs. The detailed relationship between particle deformation value and the reflectance red-shift is built. Then the crack propagation process is investigated by this method in real time. Finally, the temperature dependence of the crack propagation rate is also investigated.

2. Materials and methods

The experimental set-up, materials, and investigation procedure follow our previous work reported in Ref.  [18]. Simply speaking, colloidal photonic crystal films were fabricated from 1  vol.% aqueous suspensions of 240-nm polystyrene (PS) latex through evaporation-induced colloidal self-assembly. A CCD camera and monochromator were used synchronously to obtain real-time in-situ CCD images and reflectance spectra of CPCF. The further development in this experiment was that hot air streams at different temperatures (ranging from 100 to 180  ° C) were set to investigate the influence of temperature. The local temperatures around the monitored CPCF region were 44.8, 47, 50.7, 57.6, and 63.9  ° C, respectively.

3. Results and discussion
3.1. Real-time quantitative crack characterization from reflectance spectrum red-shift: particle deformation value

As shown in Fig.  1, along with crack propagating throughout CPCF, the peak positions of reflectance spectra shift to longer wavelengths (red-shift). These two macroscopic processes, crack propagation[5, 7, 17] and reflectance spectrum red-shift, [18] are both found to be related to microcosmic particle deformation. On one hand, the spherical particles are observed by SEM to have deform to polyhedral particles, [21– 23] and the particle deformation results in crack propagation during drying.[5, 7, 17] On the other hand, the interstices between particles decrease due to the shape change from spherical to polyhedral.[22, 23] The decrease of interstices results in the increase of particle volume fraction and then the red-shift of reflectance spectrum peak positions.[18] Therefore, the particle deformation is the connection between crack propagation and reflectance spectrum red-shift. When particles deform more seriously, more cracks are found propagating with higher density. The particle deformation value is the appropriate parameter to characterize cracks quantitatively, including the interfacial and inside cracks. What one needs to do first is to derive the particle deformation value from the reflectance spectrum red-shift. A detailed derivation follows.

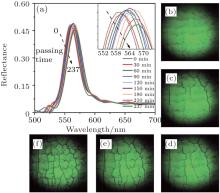Fig.  1. Real-time in-situ evolution of CPCF (a) reflectance spectra and (b)– (f) CCD images in CPCF during crack propagation.

Many experiments and simulations have revealed that mono-dispersed PS spherical particles self-assemble into a face-centered cubic (FCC) structure with the (111) planes parallel to the substrate interface during vertical deposition. The diffracted wavelength (λ ) is given by the Bragg equation[24]

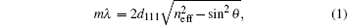
where m is the diffraction order, d111 is the inter-planar spacing of (111) planes, neff is the effective refractive index of the crystal, and θ is the incident angle. Here, θ is zero when the incident light is normal to the substrate interface. The effective refractive index of the crystal neff is given by a volume-weighted average,

where ϕ particle and ϕ water are the volume fractions occupied by PS particles and water between the particles, respectively. When m is 1, λ is the peak-position wavelength of reflectance spectrum.

With the solvent evaporating, PS particles start to deform, the particle distance and the interstices between particles decrease, [22, 23] resulting in the change of φ particle and λ .[18] To compute ϕ particle simply in our system, three assumptions are made here. First, CPCF is nearly dried out and ϕ water is regarded as zero during the deformation. Secondly, the time when the cracks begin to propagate and the reflectance spectrum begins to red-shift, is defined as zero time. At this time, CPCF is compact and ϕ particle is 0.74. The adjacent particle distance at this time is defined as R0 and can be obtained from substituting initial experimental λ into Eqs.  (1) and (2). Third, particle deformation is anisotropic due to the transverse shear stress, and the average of particle distance is considered and defined as R. The change of inter-plane spacing d111 is considered to be small during deformation, and d111 equals (2/3)1/2R0.

The lattice constant a equals 21/2R and the volume of a unit cell Vcell equals (21/2R)3. When the particle distance R decreases, Vcell decreases as well. There are four particle spheres in one unit cell and the total volume of particle spheres Vparticle equals 4(4/3)π (R0/2)3. During the deformation, the total volume of spheres Vparticle does not change, and thus φ particle becomes

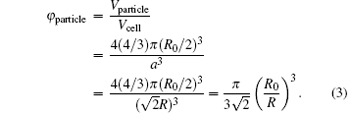
After solving Eqs.  (1)– (3) simultaneously, the relationship between λ and R is obtained. Further substituting the experimental peak-position wavelength λ at various times into Eqs.  (1)– (3), R at various times are obtained. The difference value of R with respect to R0 is the particle deformation value D. Figures  2(a)– 2(c) present the evolution of experimental peak-position wavelength λ , particle distance R, and particle deformation value D. As shown in Figs.  1 and 2, crack propagates when reflectance spectrum peak-position wavelength λ increases. Meanwhile, the particle distance R decreases and particle deformation value D increases. That is, when the particle deforms more seriously, the crack increases and becomes denser. The particle deformation value characterizes the crack, and the particle deformation process characterizes the crack propagation process.

Fig.  2. Evolution of (a) peak-position wavelength λ in experimental reflection spectra, (b) particle distance R derived from Eqs.  (1)– (3), (c) particle deformation value D.

3.2. Real-time particle deformation and crack propagation processes

As shown in Fig.  2(b), the particle distance R decreases and then keeps constant as time goes on. The particle deformation value D increases when the crack propagates. The absolute value of the R– t curve slope, which is defined as deformation rate v, decreases with time. As D is the change of R, v is also the slope of D– t curve. To obtain the regularity of the particle deformation rate, the relationship between R and v is first established and analyzed by statistical fitting analysis.

As the experimental temperatures are below the glass transition temperature of PS (Tg = 98.71  ° C shown in Fig.  A1 of Appendix  A), the particle deformation process is mainly controlled by van der Waals attraction and tensile stress in the drying film.[7] Van der Waals attraction keeps the particles together, whereas tensile stress arising from the particle deformation repulses the particles. Tensile stress is larger than van der Waals attraction; thus the direction of the resultant force is opposite to that of v; v is slowed down by the resultant force F and is a function of F, represented as v = f(F). Meanwhile, van der Waals and tensile stress both relate to R, and thus the resultant force F is a function of R, represented as F = f (R). Therefore, v is a function of R and represented as v = f(R). From the evolution of R and v in Fig.  2(b), v correlates with R. The relationship between them can be written as

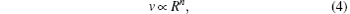
where n ≥ 0, which is undetermined. As R keeps constant after a period of time, a modified value R∞ is introduced and the relationship between R and v is represented as

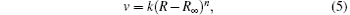
where R∞ is the particle distance at infinite time, k is the deformation rate constant, and R is the particle distance at time t.

In terms of v = dR/dt, equation  (5) becomes

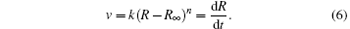
To obtain the specific relationship between R and t, n should be determined first. Considering that this is a micro-deformation process, n is suggested to be an integer. Based on statistical theory, n is finally determined to be one by the trial-and-error method. The detailed analysis and correlation test are shown in Appendix  B. Then the integration of R and t is performed and the specific relationship between R and t is

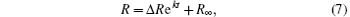
where Δ R equals (R0 − R∞ ), and R0 is the particle distance at zero time. The fitting curves and relations are shown in Figs.  3(a)– 3(e).

Fig.  3. (a)– (e) Experimental (black dot) and fitting (red line) evolution of particle distance D at different temperatures. (a) 44.8  ° C, (b) 47  ° C, (c) 50.7  ° C, (d) 57.6  ° C, (e) 63.9  ° C. (f) Fitting curves of normalized particle distance D with t at different temperatures.

As shown in Fig.  3 and Eqs.  (4)– (7), the fitting results show that the particle deformation rate v has a first-order correlation to R. With time going by, particle distance R decreases gradually, and the deformation rate v decreases as well. This is due to the existence of repulsive resultant force when the particles deform seriously. That is, when the particle deformation value D increases, the deformation rate v decreases. In macroscopic terms, the crack propagation rate slows down when the cracks become more numerous and denser. After a period of time, the deformation rate v stays stable and the crack propagation stops. This agrees intuitively with the CCD image evolution of crack.

3.3. Temperature dependence of particle deformation and crack propagation processes

To compare the tendencies of crack propagation processes at different temperatures, normalized R is plotted against t in Fig.  3(f). As shown in Fig.  3(f), the particle deformation process proceeds more slowly when temperature increases. This tendency is also reflected in the rate constant k. In Figs.  3(a)– 3(e), the rate constant k is negative due to the reaction direction; thus, the absolute values of k are considered here; | k| at different temperatures is obtained from the fitting curves, and the temperature dependence of | k| is plotted in Fig.  4. When the temperature increases, | k| decreases, indicating that the deformation rate decreases under the same conditions. The particle deformation process exhibits negative temperature dependence.

Fig.  4. Absolute variation of deformation rate constant | k| with temperature T.

The negative temperature dependence of the deformation rate can be explained as follows. As mentioned above, the resultant force F is opposite to v, and v slows down. When the temperature increases between 317.9  K and 337.1  K, van der Waals attraction increases, according to Ref.  [25]. However, the tensile stress does not change, and thus the resultant force F decreases. The estimation of the magnitude of forces is shown in Appendix  C. The decrease of resultant force F finally results in the decrease of deformation rate constant. When the temperature increases, the deformation rate changes more slowly, and the deformation rate constant decreases. In macroscopic terms, the crack propagation rate constant slows down as temperature increases, which suggests that the crack propagation rate is negatively dependent upon temperature. Meanwhile, fewer cracks are observed (as shown in Fig.  D1 in Appendix  D, in agreement with the result described in Ref.  [6] that the final crack spacing increases with increasing temperature.

Therefore, in order to achieve high quality CPCFs and reduce cracking, a certain higher temperature is preferred in drying films. These results provide a real-time quantitative way to help get deeper insight into the crack propagation mechanism, and then to control crack propagation. The detailed mechanism and theoretical analysis of crack propagation still needs to be systematically researched in further work.

4. Conclusions

A real-time quantitative optical method, the colloidal particle deformation value derived from reflectance spectra, is developed to investigate the crack propagation process. The crack propagation rate is found to slow down gradually to zero when cracks propagate. Moreover, a negative temperature dependence of the crack propagation rate is found after changing the temperature. With the temperature increasing, the crack propagation rate constant decreases. Detailed investigation reveals that the variation of the crack propagation rate constant is due to the increase of van der Waals attraction between particles, finally resulting in a decrease of resultant force. The method and findings provide new insight into the crack propagation process, which may help improve the manufacturing method and then the quality of materials.

Reference
1 Routh A F 2013 Rep. Prog. Phys. 76 046603 DOI:10.1088/0034-4885/76/4/046603 [Cited within:2]
2 Huang Y, Zhou J, Su B, Shi L, Wang J, Chen S, Wang L, Zi J, Song Y and Jiang L 2012 J. Am. Chem. Soc. 134 17053 DOI:10.1021/ja304751k [Cited within:1]
3 Cao H, Lan D, Wang Y, Volinsky A A, Duan L and Jiang H 2010 Phys. Rev. E 82 031602 DOI:10.1103/PhysRevE.82.031602 [Cited within:4]
4 Hartsuiker A and Vos W L 2008 Langmuir 24 4670 DOI:10.1021/la800137e [Cited within:1]
5 Singh K B and Tirumkudulu M S 2007 Phys. Rev. Lett. 98 218302 DOI:10.1103/PhysRevLett.98.218302 [Cited within:3]
6 Lee W P and Routh A F 2006 Ind. Eng. Chem. Res. 45 6996 DOI:10.1021/ie051256m [Cited within:5]
7 Tirumkudulu M S and Russel W B 2005 Langmuir 21 4938 DOI:10.1021/la048298k [Cited within:4]
8 Teh L K, Tan N K, Wong C C and Li S 2005 Appl. Phys. A 81 1399 DOI:10.1007/s00339-004-3095-y [Cited within:2]
9 Wong S, Kitaev V and Ozin G A 2003 J. Am. Chem. Soc. 125 15589 DOI:10.1021/ja0379969 [Cited within:1]
10 Velikov K P, van Dillen T, Polman A and van Blaaderen A 2002 Appl. Phys. Lett. 81 838 DOI:10.1063/1.1497197 [Cited within:1]
11 Shorlin K A, de Bruyn J R, Graham M and Morris S W 2000 Phys. Rev. E 61 6950 DOI:10.1103/PhysRevE.61.6950 [Cited within:1]
12 Hodges C S, Ding Y and Biggs S 2010 J. Colloid Interface Sci. 352 99 DOI:10.1016/j.jcis.2010.08.044 [Cited within:1]
13 Tarafdar S and Sinha S 2008 Ind. Eng. Chem. Res. 47 6459 DOI:10.1021/ie071375x [Cited within:1]
14 Ball P 2004 Nat. Mater. 3 851 DOI:10.1038/nmat1274 [Cited within:2]
15 Bucklow S 1999 Stud. Conserv. 44 233 DOI:10.1179/sic.1999.44.4.233 [Cited within:1]
16 Bucklow S 1997 Stud. Conserv. 42 129 DOI:10.1179/sic.1997.42.3.129 [Cited within:2]
17 Routh A F and Russel W B 1999 Langmuir 15 7762 DOI:10.1021/la9903090 [Cited within:4]
18 Lin D, Wang J, Yang L, Luo Y, Li D and Meng Q 2014 Langmuir 30 3949 DOI:10.1021/la404778p [Cited within:5]
19 Wang J, Yang L, Lin D, Luo Y, Li D and Meng Q 2012 J. Chem. Phys. 137 234111 DOI:10.1063/1.4772095 [Cited within:1]
20 Yang L, Gao K, Luo Y, Luo J, Li D and Meng Q 2010 Langmuir 27 1700 DOI:10.1021/la104338a [Cited within:1]
21 Li J, Xue L, Wang Z and Han Y 2007 Colloid. Polym. Sci. 285 1037 DOI:10.1007/s00396-007-1656-2 [Cited within:1]
22 Gates B, Park S H and Xia Y 2000 Adv. Mater. 12 653 DOI:10.1002/(SICI)1521-4095(200005)12:9<653::AID-ADMA653>3.0.CO;2-3 [Cited within:2]
23 Mazur S, Beckerbauer R and Buckholz J 1997 Langmuir 13 4287 DOI:10.1021/la970104w [Cited within:3]
24 López C, Vázquez L, Meseguer F, Mayoral R, Ocaña M and Miguez H 1997 Superlattices Microstruct. 22 399 DOI:10.1006/spmi.1996.0313 [Cited within:1]
25 Lifshitz E M 1956 Soviet Phys. 2 73 [Cited within:1]