Cite this Article
Chen Xin, Zhao Qian-Qian, Wang Xiao-Chun†, Chen Jun, Ju Xin. Linear optical properties of defective KDP with oxygen vacancy: First-principles calculations. Chinese Physics B, 24(7): 077802  
Permissions
Linear optical properties of defective KDP with oxygen vacancy: First-principles calculations
Chen Xina),b),c), Zhao Qian-Qiana),b), Wang Xiao-Chun†a),b), Chen Jund), Ju Xine)
Institute of Atomic and Molecular Physics, Jilin University, Changchun 130012, China
Jilin Provincial Key Laboratory of Applied Atomic and Molecular Spectroscopy, Jilin University, Changchun 130012, China
Collage of Chemistry, Jilin University, Changchun 130012, China
Laboratory of Computational Physics, Institute of Applied Physics and Computational Mathematics, Beijing 100088, China
Department of Physics, University of Science and Technology Beijing, Beijing 100083, China

†Corresponding author. E-mail: wangxiaochun@jlu.edu.cn

*Project supported by the National Natural Science Foundation of China (Grant No. 11474123), the Natural Science Foundation of Jilin Province, China (Grant No. 20130101011JC), and the Fundamental Research Funds for Central Universities of China.

Abstract

The linear optical properties of potassium dihydrogen phosphate (KDP) with oxygen vacancy are investigated with first-principles density functional theory calculations. We use Heyd–Scuseria–Ernzerhof (HSE06) functional to calculate the linear optical properties because of its accuracy in the band gap calculation. Compared with the perfect KDP, we found that due to the defect states located at the band gap, the defective KDP with oxygen vacancy has new optical adsorption within the energy region from 4.8 eV to 7.0 eV (the corresponding wavelength region is from 258 nm to 177 nm). As a result, the oxygen vacancy can decrease the damage threshold of KDP crystal. It may give a direction to the KDP production for laser system.

PACS: 78.20.Ci; 31.15.A–; 71.20.–b
Keyword: first-principles calculations; potassium dihydrogen phosphate; oxygen vacancy; linear optical study
1. Introduction

Potassium dihydrogen phosphate KH2PO4 (KDP) is a hydrogen-bonded ferroelectric crystal. The structures and properties of KDP have attracted wide and continuous interest. It is the very first that crystal is applied in nonlinear optics devices. It is still widely used in many nonlinear optical systems because it can grow into useful size. When temperature is above 123  K, KDP is in the paraelectric phase with a tetragonal crystal structure (I− 42d space group[1]). Davis et al. suggested that proton transport plays a major role in optical absorption.[2] The subsequent experiments using electron paramagnetic resonance (EPR) provided evidences for the proton-transport mechanism.[3] Liu et al. have calculated the electronic structure of the defective KDP with oxygen vacancy.[4] Using first-principles method, the effect of S substitution for P point defects in KDP crystal was studied by Gao et al., [5] and it is in agreement with the experimental study.[6, 7] The defect is common in the growing process of crystal. When the oxygen vacancies occur in the growing process of KDP and lead to defective KDP, the optical properties can be different for the perfect KDP. Although the KDP material is usually used as a nonlinear optical crystal, these linear optical properties affect the performance of the material in nonlinear optics, such as extrinsic absorption band within the band gap that influences the laser damage threshold of the material. The oxygen vacancies in KDP can cause the extrinsic absorption band within the band gap. This aspect of the material is less studied but important. The results are also of general interest to other oxides with oxygen vacancies, such as electrochromic material WO3.[8] The oxygen vacancy is generally referred to as a “ color center” in various oxides. First-principle study of the effects of oxygen vacancy on absorption spectrum of ZnO is also reported.[9] As far as we know, there was no first-principles study that focuses on the linear optical properties of KDP with oxygen vacancy. Then it is worthwhile to be studied.

It is well known that the band gaps of semiconductor and insulator are severely underestimated, which are calculated through the density functional theory based on generalized gradient approximation (DFT-GGA). In order to improve the calculation accuracy, the hybrid approach to constructing density functional approximations was introduced by Becke in 1993.[10] Hybridization with Hartree– Fock exchange provides a simple scheme for improving the calculation accuracy of band gap. Using the screened hybrid density functional HSE06, [11] the calculated band gap is consistent with experimental data very well.[12] The linear optical properties calculated based on accurate electronic structure will yield accurate results, such as the calculation of refractive indices.

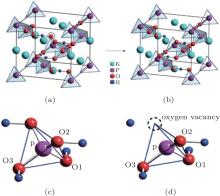
2. Computational method and details

The present work investigates the electronic structures of perfect KDP and defective KDP with oxygen vacancy, respectively, using HSE06 functional and the Vienna ab initio simulation package (VASP), which is based on the density functional theory and the projector augmented wave (PAW) representation.[13– 15] The cutoff energy of the plane-wave basis function is set to be 600  eV. We used a (4 × 4 × 4) division along the reciprocal-lattice directions in the primitive unit cell of the perfect KDP system according to the Monkhorst– Pack scheme.[16] The total energies for all systems are found to be converged to be less than 1 × 10− 5  eV/atom.[5] The KDP is in paraelectric phase with a tetragonal crystal structure (I − 42d space group). The primitive cell of perfect KDP contains 32  atoms, as shown in Fig.  1(a). In order to simulate the structure of the defective KDP with oxygen vacancy, we remove an oxygen atom from one corner of the tetrahedral PO4 unit that is in the center of the primitive cell for perfect KDP crystal, as shown in Fig.  1. All the atomic geometries were fully relaxed until the forces on all the atoms are less than 0.02  eV/Å . The lattice constants of the relaxed perfect KDP structure are a = 7.44  Å and c = 6.97  Å , which are in agreement with experimental data of a = 7.430  Å and c = 6.967  Å very well.[1] The P– O bond lengths for perfect and defective KDP are listed in Table  1.

Fig.  1. The primitive cells of (a) perfect KDP crystal and (b) defective KDP with oxygen vacancy. The circled oxygen atom is removed from the perfect structure in order to simulate oxygen vacancy. (c) Local atomic structure of the tetrahedral PO4 unit. (d) Local atomic structure of the oxygen vacancy in tetrahedral PO4.

Table 1. Bond length (in Å ) of perfect and defective KDP.
3. Results and discussion
3.1. Total density of state and partial density of state

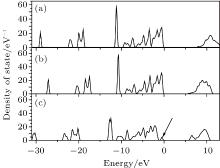
In order to compare the performances of HSE06 and GGA in electronic structure calculation, we calculate the total density of state (DOS) of perfect KDP through these two methods respectively, as shown in Figs.  2(a) and 2(b). The band gaps of perfect KDP are 7.18  eV using HSE06 (Fig.  2(a)) and 5.06  eV using GGA (Fig.  2(b)). The band gap that is calculated using HSE06 is in good agreement with the experimental data of 7.12  eV, [17] and is obviously better than the result using GGA (5.06  eV) and other results (4.35  eV using GGA, [18] 10.24  eV using mBJ-GGA, [18] 5.96  eV using GGA, [19] and 4.178  eV using GGA[20]). The total DOS of perfect KDP shows that it is a typical insulating system with a large band gap. The HSE06 functional can remarkably improve the calculation accuracy of band gap of KDP. The optical properties have a high relevance with the electronic structure. Then in order to get reliable optical properties, we decide to use HSE06 to calculate the electronic structures of perfect and defective KDP. The band gap of defective KDP with oxygen vacancy is 5.62  eV, which is much lower than 7.18  eV (perfect KDP). This fact is due to the fact that the new oxygen vacancy defect states are mainly located at the band gap, which is marked by the arrow in Fig.  2(c).

Fig.  2. The densities of states for (a) perfect KDP calculated using HSE06, (b) perfect KDP calculated using GGA, and (c) defective KDP calculated using HSE06. Solid line indicated by the arrow is defect state. The Fermi energy level is at 0 eV.

Figure  3 shows the orbital-resolved and atom-resolved density of states for perfect KDP and defective KDP with oxygen vacancy. In perfect KDP, each O atom is located at the same environment and the orbital-resolved DOS of each O atom is identical. In sharp contrast, the O1, O2, and O3 of defective KDP show large difference between each other due to the breaking of [PO4]3− tetrahedron symmetry. The defect state is generated by s-state, p-state of P, and p-state of O1. The results indicate that the removal of O atoms causes electronic charge redistribution near the defect site. Electrons accumulate near the Fermi level in s-state, p-state of P, and p-state of O1. The defect states (indicated by the arrows, in Figs.  3(e) and 3(f)) induce that the band gap decreases from 7.18  eV (perfect KDP) to 5.62  eV (defective KDP). More details about charge redistribution are illustrated in Fig.  4.

Fig.  3. (a)– (d) PDOS of perfect KDP, (d)– (h) PDOS of KDP with oxygen vacancy. O1, O2, and O3 correspond to the oxygen atom in Fig.  1. The Fermi energy level sets at 0  eV.

Fig.  4. Contour plots of the differences of electron charge densities for (b) perfect KDP and (c) defective KDP with oxygen vacancy. The plotted plane for (b) and (c) is along the (001) plane and cross the center P atom, as shown in (a). Contour plots of the differences of electron charge densities for (e) perfect KDP and (f) defective KDP with oxygen vacancy, along the plane that contains O– H– O– P chain shown in panel (d). In the contour plots of charge density differences, K, P O, and H atoms are denoted with grey, pink, red, and blue balls. The black rectangles in panels (b) and (c) indicate one unit cell. Solid and dashed lines in panels (b), (c), (e), and (f) correspond to Δ ρ > 0 and Δ ρ < 0, respectively.

3.2. Contour plots of the differences of electron charge densities

In order to understand the nature of atomic interaction in KDP crystal, the contour plots of differences of electron charge densities are shown in Fig.  4. The charge density difference is defined as the differences between the KDP crystal and the superposition of atomic charge densities, i.e., Δ ρ = ρ (KDP) − Σ ρ (atom). The contour plot of the charge density differences helps to visualize the characteristics of bonding. Figure  4(a) shows the location of plotted planes for Figs.  4(b) and 4(c). It is along the (001) plane that crosses the P atom at the center of the primitive cell, and the oxygen vacancy is above this plane. Figure  4(b) shows the contour plot of the differences of electron charge densities of perfect KDP crystal. The four P– O bonds are symmetric perfectly, and the length of each covalent bond is 1.56  Å . The formation of oxygen vacancy breaks the symmetry of PO4 tetrahedron as well as the symmetry of charge density difference around the center P atom, as shown in Fig.  4(c). Due to the defect in PO4 tetrahedral with oxygen vacancy, the charge density around K atoms also becomes slightly asymmetric and then induces a weak dipole around each K atom. In order to show more information around the oxygen vacancy, the plotted plane for Figs.  4(e) and 4(f) contains the location of oxygen vacancy, as shown in Fig.  4(d). The charge contour plot patterns that contain O– H– O– P chain without and with oxygen vacancy are shown in Figs.  4(e) and 4(f), respectively. In contrast with the perfect KDP (Fig.  4(e)), the electron charge density of defective KDP with oxygen vacancy is obviously redistributed. Figure  4(f) shows that the charge density between the H atom and the left neighbor O atom accumulates markedly, which means the interaction between the H and left O atom becomes stronger than that of Fig.  4(e). The H atom slightly moves left and approaches the left O atom, which is identified as a proton transfer. The three P– O bonds (1.63  Å ) of defective KDP become longer than that (1.56  Å ) of perfect KDP, as listed in Table  1. This is due to the fact that the lone pair electrons of P atom repulse three O atoms. Then the oxygen vacancies weaken the other three bonds between P and O atoms. The formation of the defect state induced by oxygen vacancy can be understood as follows. The removal of the O at the origin effectively creates a repulsive potential for the electron at the core of the vacancy, [8] which drives the “ extra” electron of the nearest P away from the vacancy site along the lowest energy direction [110].

3.3. Optical properties

We derive the linear optical properties of perfect KDP and defective KDP with oxygen vacancy from the reliable electronic structures of these two systems, which are calculated using HSE06 method. A linear response of a material to an electromagnetic radiation is described by the dielectric function ε (ω ). The dielectric function ε (ω ) (Fig.  5) can be described by

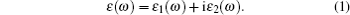Fig.  5. Complex dielectric functions of (a) perfect KDP and (b) defective KDP with oxygen vacancy.

The frequency-dependent imaginary part of the dielectric function can be calculated by the momentum matrix elements from the occupied and unoccupied wave functions within the selection rules. The real part of the dielectric function is obtained using the Kramers– Kronig relations

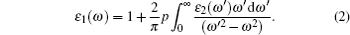All other linear optical properties can be obtained from the dielectric function.

(i) Absorption coefficient:

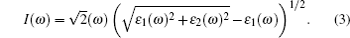(ii) Reflectivity:

(iii) Refractive index:

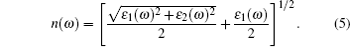(iv) Optical conductivity:

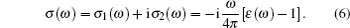(v) Extinction coefficient:

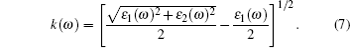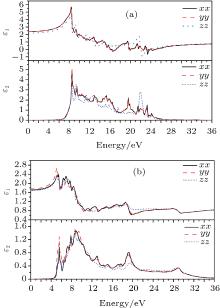
The real part ε 1 and the imaginary part ε 2 of the dielectric function of perfect KDP and defective KDP with oxygen vacancy are shown in Fig.  5, respectively. Because of the symmetry of perfect KDP crystal, the variation trend of ε xx (dielectric function of the KDP in xx direction) curve is consistent with that of ε yy for both the real part ε 1 and the imaginary part ε 2 of the dielectric function. However, in the defective KDP with oxygen vacancy, the structure symmetry is broken, the variation trend consistency between ε xx and ε yy disappears. For example, at 5.1  eV, the peak of ε 1(yy) of defective KDP with oxygen vacancy is obviously higher than that of ε 1(xx), as shown in Fig.  5(b). Compared with Fig.  5(a), the peak positions with the lowest energy in Fig.  5(b) move to lower energy, and thus redshift occurs. For example, the real part ε 1 peak with the lowest energy in Fig.  5(a) is located at 8.5  eV. However in Fig.  5(b), the real part ε 1 peak with the lowest energy is located at 5.6  eV, which is 2.9  eV lower than that in Fig.  5(a). These facts originate in the defect states of oxygen vacancy.

The linear optical properties of perfect KDP and defective KDP with oxygen vacancy are shown in Fig.  6. We find that for the defective KDP, the energy region in which the cure of each optical property is not flat becomes wider than that for perfect KDP. For example, the absorption coefficient I(ω ) of the defective KDP is not flat in the energy region from 4.8  eV to 36  eV, which is wider than that from 6.9  eV to 33.9  eV of perfect KDP. It means that compared with perfect KDP, the optical properties of defective KDP change greatly, e.g., the absorption band of defective KDP becomes wider than that of perfect KDP. The peak with the lowest energy for each optical property curve appears to be red shifted. For example, the peak with the lowest energy of absorption coefficient I(ω ) for defective KDP is located at 5.58  eV that is lower than that for the perfect KDP (8.52  eV). The absorption coefficient I(ω ) begins to rise at 4.8  eV (corresponding to 258  nm wavelength), as shown in Fig.  6(b). However, the perfect KDP begin to have optical absorption at about 7.0  eV (corresponding to 177  nm wavelength). It means that KDP with oxygen vacancy begins to absorb the energy of the laser irradiation from 4.8  eV which is much lower than that for the perfect KDP. The energy accumulation in KDP crystal will damage the stabilities of structure and optical properties of crystal. Hence, the oxygen vacancy in KDP reduces the damage threshold of KDP crystal from 7.0  eV to 4.8  eV. The origin of the absorption at 4.8  eV of KDP crystal with oxygen vacancy is related to the band gap absorption caused by the defect states, because the defect energy level for oxygen vacancy in defective KDP leads to a narrower band gap of 5.62  eV compared with that for perfect KDP (7.18  eV). The reflectivity R(ω ) is also an important property of a crystal and it can decide the quality of optics devices. The dramatic rise of R(ω ) reduces the optical transmittance of the KDP crystal. For the defective KDP with oxygen vacancy, the reflectivity begins to rise steeply at about 4.0  eV. However, the reflectivity of perfect KDP begins to rise steeply at about 7.5  eV. The extinction coefficient k(ω ) and optical conductivity σ 1(ω ) varies as nearly same as the absorption coefficient. The I(ω ), k(ω ), and σ 1(ω ) all reflect the absorption property of a crystal. The above facts reveal that the oxygen vacancy in KDP reduces the quality of KDP as a laser device system, and leads to a new energy region of optical absorption which is lower than 7.0  eV. The new optical absorption can cause energy accumulate around the defect site in the KDP crystal, and then remarkably decrease the damage threshold energy threshold of KDP crystal. Electrons near the defect site are excited to higher energy level in the wavelength range of photon absorption. Laser-induced excited electrons relax to the ground state and the released energy causes the strong lattice vibration. The strong lattice vibration can cause the laser damage. Then the defect site with unstable structure can be the origin of damage under the strong lattice vibration.

Fig.  6. Absorption coefficient, refractive index, optical conductivity, extinction coefficient, and reflectivity of (a) the perfect KDP and (b) the defective KDP with oxygen vacancy.

KDP is a uniaxial crystal with negative birefringence (no > ne), nxx = nyy = no, and nzz = ne.[22] The refractive indices of perfect KDP calculated with HSE06, experimentally measured value and other calculation results are listed in Table  2. Results obtained with HSE06 are better in agreement with experimental value than other calculation results. In view of the facts above, the performance of HSE06 in optical properties calculation is reliable.

Table 2. Refractive index of perfect KDP for selective wavelength (values (in%) in parentheses are difference from experimental values).
4. Conclusion

In conclusion, the electronic structure of perfect KDP and defective KDP with oxygen vacancy are investigated with screened hybrid density functional HSE06. Then based on these reliable data, the optical properties of perfect KDP and defective KDP with oxygen vacancy are derived. The defect states induced by oxygen vacancy are mainly located in the band gap, and reduce the band gap from 7.18  eV (for perfect KDP) to 5.62  eV. The defect states around Fermi level are mainly contributed by p and d electrons of P atom and s electrons of O1 atom. We compare the differences of charge density of perfect KDP and defective KDP to study the changes of atomic interaction. We find that the oxygen vacancy breaks the symmetry of the PO4 tetrahedral and causes the remarkable redistribution of electron charge around P atom, and then weakens the interactions between P and O atoms. Compared with the linear optical properties of the perfect KDP, the absorption coefficient I(ω ) of defective KDP begins to have unwanted absorption at 4.8  eV (corresponding to 258  nm wavelength), which is lower than 7.0  eV (corresponding to 177  nm wavelength) of perfect KDP. It means that the defective KDP with oxygen vacancy will begin to absorb the energy of laser radiation within the energy region from 4.8 to 7.0  eV, where the perfect KDP does not begin to absorb the energy of laser. Then the oxygen vacancy in KDP will lead to the lower damage threshold for the defective KDP than perfect KDP. Such a finding is expected to give a direction to the process of producing KDP crystal for laser system. Particular attention should be paid on preventing oxygen vacancy formation during the growing of KDP crystal, in order to avoid the extra optical absorption band caused by oxygen vacancy.

Acknowledgments

Part of the calculations was performed in the High Performance Computing Center (HPCC) of Jilin University. The authors also acknowledge Dr. Sheng-Peng Zhou for writing the data handling program.

Reference
1 Nelmes R J, Meyer G M and Tibballs J E 1982 J. Phys. C: Solid State Phys. 15 59 DOI:10.1088/0022-3719/15/1/005 [Cited within:2]
2 Davis J E, Hughes Jr R S and Lee H W H 1993 Chem. Phys. Lett. 207 540 DOI:10.1016/0009-2614(93)89044-I [Cited within:1]
3 Setzler S D, Stevens K T, Halliburton L E, Yan M, Zaitseva N P and DeYoreo J J 1998 Phys. Rev. B 57 2643 DOI:10.1103/PhysRevB.57.2643 [Cited within:1]
4 Liu C S, Hou C J, Kioussis N, Demos S G and Radousky H B 2005 Phys. Rev. B 72 134110 DOI:10.1103/PhysRevB.72.134110 [Cited within:1]
5 Gao H, Sun X, Liu B A, Xu M X, Hu G H, Xu X G and Zhao X 2010 Chin. Phys. Lett. 27 073101 DOI:10.1088/0256-307X/27/7/073101 [Cited within:2]
6 Hu G H, Zhao Y A, Sun S T, Li D W, Liu X F, Sun X, Shao J D and Fan Z X 2009 Chin. Phys. Lett. 26 097802 DOI:10.1088/0256-307X/26/9/097802 [Cited within:1]
7 Hu G H, Zhao Y A, Sun S T, Li D W, Sun X, Shao J D and Fan Z X 2009 Chin. Phys. Lett. 26 087801 DOI:10.1088/0256-307X/26/8/087801 [Cited within:1]
8 Karazhanov S Z, Zhang Y, Wang L W, Mascarenhas A and Deb S 2003 Phys. Rev. B 68 233204 DOI:10.1103/PhysRevB.68.233204 [Cited within:2]
9 Hou Q Y, Guo S Q and Zhao C W 2014 Acta Phys. Sin. 63 147101 DOI:10.7498/aps.63.147101(in Chinese) [Cited within:1]
10 Becke A D 1993 J. Chem. Phys. 98 1372 DOI:10.1063/1.464304 [Cited within:1]
11 Heyd J, Scuseria G E and Ernzerhof M 2003 J. Chem. Phys. 118 8207 DOI:10.1063/1.1564060 [Cited within:1]
12 Park S, Lee B, Jeon S H and Han S 2011 Current Appl. Phys. 11 S337 DOI:10.1016/j.cap.2010.09.008 [Cited within:1]
13 Kresse G and Furthmüller J 1996 Comput. Mater. Sci. 6 15 DOI:10.1016/0927-0256(96)00008-0 [Cited within:1]
14 Kresse G and Furthmüller J 1996 Phys. Rev. B 54 11169 DOI:10.1103/PhysRevB.54.11169 [Cited within:1]
15 Kresse G and Hafner J 1993 Phys. Rev. B 47 558 DOI:10.1103/PhysRevB.47.558 [Cited within:1]
16 Monkhorst H J and Pack J D 1976 Phys. Rev. B 13 5188 DOI:10.1103/PhysRevB.13.5188 [Cited within:1]
17 Dimitriev G Gurzaddyan G G Nikogosyan D N 1997 Hand book of Nonlinear Optical Crystals Berlin Springer DOI:10.1007/978-3-540-68392-6 [Cited within:1]
18 Aliabad H A R, Fathabadi M and Ahmad I 2013 Int. J. Quant. Chem. 113 865 DOI:10.1002/qua.24258 [Cited within:2]
19 Zhang Q, Chen F, Kioussis N, Demos S G and Radousky H B 2001 Phys. Rev. B 65 024108 DOI:10.1103/PhysRevB.65.024108 [Cited within:1]
20 Lin Z S, Wang Z Z, Chen C T and Lee M H 2003 J. Chem. Phys. 118 2349 DOI:10.1063/1.1533734 [Cited within:1]
21 Carr C W, Radousky H B and Demos S G 2003 Phys. Rev. Lett. 91 127402 DOI:10.1103/PhysRevLett.91.127402 [Cited within:1]
22 Zhu S J, Wang S L, Liu L, Wang D L, Li W D, Huang P P and Xu X G 2014 Acta Phys. Sin. 63 107701 DOI:10.7498/aps.63.107701(in Chinese) [Cited within:1]
23 Zernike J F 1964 J. Opt. Soc. Am. 54 1215 DOI:10.1364/JOSA.54.001215 [Cited within:1]