Cite this Article
Qiu Jian-Hua†, Wang Xiu-Qin, Yuan Ning-Yi, Ding Jian-Ning‡. Piezoelectric and electro optic properties of tetragonal (1 − x)Pb(Mg1/3Nb2/3)O3− xPbTiO3 single crystals by phenomenological theory . Chinese Physics B, 24(7): 077701  
Permissions
Piezoelectric and electro optic properties of tetragonal (1 − x)Pb(Mg1/3Nb2/3)O3− xPbTiO3 single crystals by phenomenological theory
Qiu Jian-Hua†, Wang Xiu-Qin, Yuan Ning-Yi, Ding Jian-Ning‡
Center for Low-dimensional Materials, Micro-nano Devices and System, Changzhou University, Changzhou 213164, China

†Corresponding author. E-mail: jhqiu@cczu.edu.cn

‡Corresponding author. E-mail: dingjn@cczu.edu.cn

*Project supported by the National Natural Science Foundation of China (Grant No. 51335002), the Changzhou Science and Technology Project, China (Grant No. CJ20130022), and the Priority Academic Program Development of Jiangsu Higher Education Institutions, China.

Abstract

An eighth-order Landau–Devonshire theory is constructed to investigate the piezoelectric and electro–optic properties of tetragonal (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals ( x = 0.38 and x = 0.4). The dielectric stiffness coefficients of the Landau potential are obtained by fitting to the dielectric properties and the phase transition temperature between cubic phase and tetragonal phase. It is indicated that tetragonal (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals have the first-order cubic-tetragonal phase transitions. The dielectric constants are in great agreement with the experimental results. The piezoelectric coefficients d33 and d31 at room temperature are about 145 pC/N and −62 pC/N respectively which are smaller than that of (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals around the morphotropic phase boundary. Moreover, tetragonal (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals have the linear electro–optic coefficients rc = 33.7 pm/V and rc = 28.8 pm/V for x = 0.38 and x = 0.4, respectively which are in accordance with the measurements.

PACS: 77.22.–d; 77.65.Bn; 78.20.Jq
Keyword: dielectric property; piezoelectric property; electrooptic effect
1. Introduction

Recently, ferroelectric (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 and (1 − x)Pb(Zn1/3Nb2/3)O3– xPbTiO3 single crystals have attracted a great deal of attention due to their large piezoelectric properties, high electromechanical coupling factors, and field-induced strain response.[1– 8] Moreover, the large piezoelectric coefficient is attractive for the photorefractive effect because the field-induced strain enhances the refractive index change via the photoelastic effect.[9] Therefore, ferroelectric single crystals with high electro– optic coefficients have practical applications in many optical devices, such as electro– optic modulators, switches, frequency shifters and light valves.

Experimentally, the photorefractive properties of tetragonal 0.62Pb(Mg1/3Nb2/3)O3− 0.38PbTiO3 single crystals have been investigated by the two-wave mixing experiment.[9] The effective electro– optic coefficient reff = 70  pm/V was observed at room temperature. On the other hand, the electro– optic measurements were performed by using the Senarmont compensator method at room temperature and the linear electro– optic coefficients of tetragonal 0.62Pb(Mg1/3Nb2/3)O3− 0.38PbTiO3 single crystals were 41– 43  pm/V at the wavelength of 633  nm.[10– 12] In addition, the electro– optic effects of (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals with different structures were measured. Tetragonal 0.62Pb(Mg1/3Nb2/3)O3− 0.38PbTiO3 single crystals poled along the ⟨ 001⟩ direction shown r33 = 70  pm/V, and rhombohedral 0.67Pb(Mg1/3Nb2/3)O3− 0.33PbTiO3 single crystals poled along the ⟨ 111⟩ direction had r33 = 107  pm/V.[13] The larger electro– optic coefficient of rhombohedral 0.67Pb(Mg1/3Nb2/3)O3− 0.33PbTiO3 single crystals attributed to their high piezoelectric properties.

Many papers on the electro– optic effect were reported experimentally, however, there have hardly been any publications about theoretical researches of an electro– optic effect in (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals. This is due to the complexity of the phase transitions of (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals that no theory can be applied to explain the physical properties very well. Therefore, we suggest an eighth-order Landau– Dovenshire phenomenological theory to investigate the electro– optic effect of (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals because of its success in explaining the phase transition and electro– optic effect of BaTiO3 and (Ba1− xSrx)TiO3.

Here, an eighth-order Landau– Dovenshire theory is constructed by fitting to the phase transition temperature and dielectric properties of (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals; then the piezoelectric coefficients and electro– optic effect are investigated. Theoretical calculations indicate that the observations of piezoelectric and electro– optic coefficients can be explained by the eighth-order theory.

2. Model and method

Ferroelectric (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals (x = 0.38 and x = 0.4) have the phase transition from cubic paraelectric phase to tetragonal phase.[14, 15] Given the spontaneous polarization and the applied electric field are along the [001] direction, the eighth-order thermodynamical potential can be given as a polynomial of the polarization component P3 under mechanical stress-free boundary condition[16]

where α 1, α 11, α 111, and α 1111 are dielectric stiffness coefficients. The temperature dependence of ferroelectricity is mainly governed by the dielectric stiffness coefficient α 1, and the other dielectric stiffness coefficients may be taken as temperature-independent parameters. α 1 = (T − T0)/2ε 0C obeys the Curie– Weiss law. Here, T0 and C are the Curie– Weiss temperature and constant respectively, and ε 0 is the dielectric constant of free space. In order to investigate the thermodynamic properties, these dielectric stiffness coefficients should be obtained firstly. Therefore, α 1 is fitted to the dielectric constant of the C phase by using the Curie– Weiss law. α 11, α 111, and α 1111 are fitted to the phase transition temperature from the cubic phase to the tetragonal phase, and to the dielectric constant of the tetragonal phase. The dielectric stiffness coefficients obtained in this work are listed in Ref.  [17].

The polarization of the tetragonal phase is determined by the equilibrium condition ∂ G/∂ P3 = 0, which is

The dielectric constant ε 33 can be given by differentiating the thermodynamic potential G

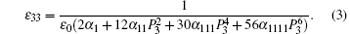
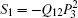
The piezoelectric coefficient dln can be derived by the relation dln = ∂ Sn/∂ El, where Sn is the spontaneous strain.[18] Therefore, the piezoelectric coefficients d33 = ∂ S3/∂ E3 and d31 = ∂ S1/∂ E3 are calculated with the strain and , [15] where Q11 and Q12 are electrostrictive coefficients.

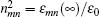
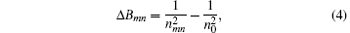
The optic property of crystal is generally described by the refractivity nmn, which is along the spontaneous polarization. The relation between optic frequency permittivity and refractivity ascribed to the electro– optic effect is . Defining , the shifting of refractivity is written as

where n0 is the refractive index of the single crystals without applying an electric field.

On the other hand, the refractivity is also described by the independent parameter P which is the sum of spontaneous polarization PS and the field-induced polarization PE. Therefore, the variety of refractivity can be given as a function of field-induced polarization PE

where Pp and Pq are the field-induced polarization, f is the linear polarization-optic coefficient, and g is the quadratic polarization-optic coefficient. The linear polarization-optic coefficient f and quadratic polarization-optic coefficient g, which are the functions of spontaneous polarization PS, can be deduced from Eqs.  (4) and (5).

The relation between linear electro– optic coefficient rc and linear polarization-optic coefficient f can be found by[19]

3. Results and discussion

The spontaneous polarizations Ps of tetragonal (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals (x = 0.38 and x = 0.4) are presented in Fig.  1. As shown in the figure, the cubic-tetragonal phase transitions occur at 175  ° C and 182  ° C for 0.62Pb(Mg1/3Nb2/3)O3− 0.38PbTiO3 and 0.6Pb(Mg1/3Nb2/3)O3− 0.4PbTiO3 single crystals respectively, which are in accordance with the measurements of 174  ° C[14] and 190 ± 5  ° C.[15] The polarizations increase as the temperature cools down to room temperature, and are discontinuous at the phase transition temperature, which indicates that the phase transitions from the cubic phase to the tetragonal phase are of the first-order. These results are in agreement with the experimental measurements.[15, 20] Moreover, the polarization of 0.6Pb(Mg1/3Nb2/3)O3− 0.4PbTiO3 single crystals is larger than that of 0.62Pb(Mg1/3Nb2/3)O3− 0.38PbTiO3 single crystals because of possessing more ferroelectric PbTiO3 composition.

Fig.  1. The temperature dependence of spontaneous polarizations of (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals.

Figure  2 shows the temperature dependence of dielectric constants ε 33 in (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals. The scattered dots are experimental measurements resulted from Refs.  [14] and [15] for x = 0.38 and x = 0.4 respectively. The solid lines are the theoretical results. The dielectric constants in the cubic phase are fitted by the Curie– Weiss law ε = C/(T − T0), and in the tetragonal phase are fitted using Eq.  (3). Due to the relaxor behavior, the dielectric constants of (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals with less PT composition have a strong deviation to the Curie– Weiss law above the Curie temperature. However, for x > 0.35, (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals show a weak relaxor behavior.[15] Therefore, the dielectric constants above the Curie temperature are fitted to the Curie– Weiss law for simplicity. The dielectric constants are discontinuous at the phase transition temperature, which show the first-order phase transitons. The room temperature dielectric constants of 0.62Pb(Mg1/3Nb2/3)O3− 0.38PbTiO3

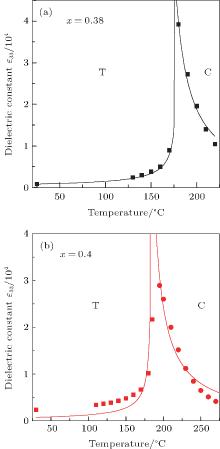Fig.  2. Dielectric constants ε 33 of (1 − x)Pb(Mg1/3 Nb2/3)O3– xPbTiO3 single crystals. Solid lines are the theoretical results calculated by eighth-order Landau– Dovenshire theory. Scattered dots are experimental observations originated from Ref.  [14] for x = 0.38 (a), and Ref.  [15] for x = 0.4 (b).

and 0.6Pb(Mg1/3Nb2/3)O3− 0.4PbTiO3 single crystals are 834 and 713 respectively, which are in agreement with the observations of 734– 828[3, 9, 14] and 420.[21] In a word, the calculations of dielectric constants for (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals are in accordance with the experimental results. Most importantly, the dielectric constants of (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals are much larger than those of conventional ferroelectrics, such as BaTiO3[16] and PbTiO3.[22]

The piezoelectric coefficients d33 and d31 as a function of temperature are plotted in Fig.  3 for (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals. The definition of piezoelectric coefficient dln shown in Section  2 is associated with the electrostrictive coefficients Qi, j. Therefore, the electrostrictive coefficients Q11 = 0.056  m4/C2 and Q12 = − 0.024  m4/C2 are taken into account in the calculations for (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals (x = 0.38 and x = 0.4).[23] It is worthwhile noting that another critical piezoelectric coefficient d15 is important to (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals and a high shear piezoelectric behavior was observed in tetragonal 0.58Pb(Mg1/3Nb2/3)O3− 0.42PbTiO3 single crystal.[24] However, piezoelectric coefficient d15 cannot be obtained by our eighth-order theory because of the electric field applied along the [001] direction. As seen from the figure, the piezoelectric coefficients d33 and d31 both increase with the temperature increasing. The piezoelectric coefficients d33 at room temperature are 145  pC/N and 143  pC/N for 0.62Pb(Mg1/3Nb2/3)O3− 0.38PbTiO3 and 0.6Pb(Mg1/3Nb2/3)O3− 0.4PbTiO3 single crystals respectively, which are comparable with the measurements of 210– 400  pC/N[14, 20, 25, 26] and 300  pC/N.[27] The piezoelectric coefficient d31 of 0.62Pb(Mg1/3Nb2/3)O3− 0.38PbTiO3 single crystals is − 62  pC/N which is in great agreement with the experimental result of − 60  pC/N.[11, 13] Furthermore, the piezoelectric coefficients of 0.62Pb(Mg1/3Nb2/3)O3− 0.38PbTiO3 and 0.6Pb(Mg1/3Nb2/3)O3− 0.4PbTiO3 single crystals are about the same. Tetragonal (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals have large piezoelectric properties, however, they are smaller than those of (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals, which are around the morphotropic phase boundary. Because they have the complicated crystal structure and the larger piezoelectric coefficients, they could be attributed to the relaxor ferroelectric state, [20] polydomain crystal structure, [25] or the polarization rotation induced by an electric field.[28]

Fig.  3. Piezoelectric coefficients d33 and d31 of (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals.

By utilizing Eqs.  (4)– (6), the linear electro– optic coefficients rc of (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals (x = 0.38 and x = 0.4) are obtained and shown in Fig.  4. The linear electro– optic coefficients increase as the temperature increases. However, the linear electro– optic coefficients are nearly invariant at the low temperature, which are very similar to those of the measurement.[12] The linear electro– optic coefficient of 0.62Pb(Mg1/3Nb2/3)O3− 0.38PbTiO3 single crystals is larger than that of 0.6Pb(Mg1/3Nb2/3)O3− 0.4PbTiO3 single crystals. Moreover, the 0.62Pb(Mg1/3Nb2/3)O3− 0.38PbTiO3 single crystals have a linear electro– optic coefficient of 33.7  pm/V, which is in agreement with the experimental results of 41– 43.3  pm/V.[10– 12]

Fig.  4. The linear electro– optic coefficients of (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals as a function of temperature.

4. Conclusion

In this paper, an eighth-order Landau– Devonshire theory is constructed to investigate the ferroelectric, dielectric, piezoelectric, and electro– optic properties of (1 − x)Pb(Mg1/3Nb2/3)O3– xPbTiO3 single crystals (x = 0.38 and x = 0.4). By fitting to the experimental measurements, the dielectric stiffness coefficients are obtained. Theoretical calculations indicate that the experimental observations of dielectric constants, piezoelectric coefficients, and linear electro– optic coefficients are explained very well by the eighth-order Landau– Devonshire theory. Therefore, these results could be useful for further experimental studies.

Reference
1 Li X B and Luo H S 2010 J. Am. Ceram. Soc. 93 2915 DOI:10.1111/jace.2010.93.issue-10 [Cited within:1]
2 Noheda B, Cox D E, Shirane G, Gao J and Ye Z G 2002 Phys. Rev. B 66 054104 DOI:10.1103/PhysRevB.66.054104 [Cited within:1]
3 Feng Z Y, Zhao X Y and Luo H S 2006 J. Am. Ceram. Soc. 89 3437 DOI:10.1111/jace.2006.89.issue-11 [Cited within:1]
4 Fang S X, Tang D Y, Chen S M, Zhang H and Liu Y L 2015 Chin. Phys. B 24 027802 DOI:10.1088/1674-1056/24/2/027802 [Cited within:1]
5 Li F, Zhang S J, Xu Z, Wei X Y, Luo J and Shrout T R 2010 J. Appl. Phys. 108 034106 DOI:10.1063/1.3466978 [Cited within:1]
6 He C J, Xu F, Wang J M, Du C L, Zhu K J and Liu Y W 2011 J. Appl. Phys. 110 083513 DOI:10.1063/1.3654142 [Cited within:1]
7 He C J, Fu X D, Xu F, Wang J W, Zhu K J, Du C L and Liu Y W 2012 Chin. Phys. B 21 054207 DOI:10.1088/1674-1056/21/5/054207 [Cited within:1]
8 Park S E and Shrout T R 1997 J. Appl. Phys. 82 1804 DOI:10.1063/1.365983 [Cited within:1]
9 He C J, Zhou Z X, Liu D J, Zhao X Y and Luo H S 2006 Appl. Phys. Lett. 89 261111 DOI:10.1063/1.2424669 [Cited within:3]
10 Wan X M, Xu H Q, He T H, Lin D and Luo H S 2003 J. Appl. Phys. 93 4766 DOI:10.1063/1.1561991 [Cited within:2]
11 He C J, Ge W W, Zhao X Y, Xu H Q, Luo H S and Zhou Z X 2006 J. Appl. Phys. 100 113119 DOI:10.1063/1.2384813 [Cited within:1]
12 Wan X M, Wang D Y, Zhao X Y, Luo H S, Chan H L W and Choy C L 2005 Solid State Commun. 134 547 DOI:10.1016/j.ssc.2005.02.033 [Cited within:3]
13 Jeong D Y, Lu Y, Sharma V, Zhang Q M and Luo H S 2003 Jpn. J. Appl. Phys. 42 4387 DOI:10.1143/JJAP.42.4387 [Cited within:2]
14 Feng Z Y, Zhao X Y and Luo H S 2004 J. Phys. : Condens. Matter 16 6771 DOI:10.1088/0953-8984/16/37/013 [Cited within:5]
15 Noblanc O, Gaucher P and Calvarin G 1996 J. Appl. Phys. 79 4291 DOI:10.1063/1.361865 [Cited within:6]
16 Li Y L, Cross L E and Chen L Q 2005 J. Appl. Phys. 98 064101 DOI:10.1063/1.2042528 [Cited within:2]
17 The list of the parameters of G (in SI units, the temperature T in °C) used in the calculations. For x = 0. 38: T0 = 162. 1, C = 7. 13 × 105, α11 = −1. 7 × 108, α111 = 6. 9 × 109, and α1111 = 1. 4 × 1010. For x = 0. 4: T0 = 175. 6, C = 5. 95 × 105, α11 = −1 × 108, α111 = 3. 9 × 109, and α1111 = 1 × 1010 [Cited within:1]
18 Emelyanov A Y, Pertsev N A and Kholkin A L 2002 Phys. Rev. B 66 214108 DOI:10.1103/PhysRevB.66.214108 [Cited within:1]
19 Di Domenico M and Wemple S H 1969 J. Appl. Phys. 40 720 DOI:10.1063/1.1657458 [Cited within:1]
20 Zhao X Y, Wang J, Chew K H, Chan H L W, Choy C L, Yin Z W and Luo H S 2004 Mater. Lett. 58 2053 DOI:10.1016/j.matlet.2003.12.024 [Cited within:3]
21 Tang Y X, Wan X M, Zhao X Y, Pan X M, Lin D, Luo H S, Sun J L, Meng X J and Chu J H 2005 J. Appl. Phys. 98 084104 DOI:10.1063/1.2106014 [Cited within:1]
22 Huan M J, Furman E, Jang S J, Mckinstry H A and Cross L E 1987 J. Appl. Phys. 62 3331 DOI:10.1063/1.339293 [Cited within:1]
23 Li F, Jin L, Xu Z, Wang D W and Zhang S J 2013 Appl. Phys. Lett. 102 152910 DOI:10.1063/1.4802792 [Cited within:1]
24 Li F, Zhang S J, Xu Z, Wei X Y and Shrout T R 2011 Adv. Funct. Mater. 21 2118 DOI:10.1002/adfm.v21.11 [Cited within:1]
25 Feng Z Y, Zhao X Y and Luo H S 2006 J. Appl. Phys. 100 024104 DOI:10.1063/1.2220490 [Cited within:2]
26 Wan X M, Luo H S, Wang J, Chan H L W and Choy C L 2004 Solid State Commun. 129 401 DOI:10.1016/j.ssc.2003.10.025 [Cited within:1]
27 Emelyanov A S, Raevskaya S I, Savenko F I, Topolov V Y, Raevski I P, Turik A V and Kholkin A L 2007 Solid State Commun. 143 188 DOI:10.1016/j.ssc.2007.02.003 [Cited within:1]
28 Guo Y P, Luo H S, Ling D, Xu H Q, He T H and Yin Z W 2003 J. Phys. : Condens. Matter 15 L77 DOI:10.1088/0953-8984/15/2/110 [Cited within:1]