Currently, magnetic materials showing a large magnetocaloric effect (MCE) have become a topic of growing interest, since the magnetic refrigeration technique based on the MCE is regarded as a promising alternative to the conventional vapor-cycle refrigeration.^{[1, 2]} A large MCE is always observed in magnetostructural transition materials where the contribution of lattice entropy to structural transition is considerable.^[3] Among such materials, La– Fe– Si compounds with NaZn₁₃-type structure (the 1:13 phase) are one of the most promising magnetic refrigerants, as they hold several advantages towards magnetic cooling applications, such as low cost and nontoxic consisting elements, high magnetic moment and MCE, relatively low driven field and little hysteresis, and tunable Curie temperature (T_c) by elemental substitution or interstitial insertion.^{[4– 10]} The solidified microstructure of as-cast stoichiometric La(Fe, Si)₁₃ compounds usually consists of secondary phases including α -Fe and LaFeSi (the 1:1:1 phase). It is required at least one week homogenization around 1323 K to obtain the single 1:13 phase in La(Fe, Si)₁₃ bulk alloys.^[11] Due to this energy consuming and low efficient preparation, alternative techniques, such as melt spinning, ^[12] strip casting, ^[13] and powder metallurgical processing, ^{[14, 15]} have been developed to shorten annealing time. Till now, almost all previous studies concerned the synthesis methods, magnetic entropy change (Δ S), and adiabatic temperature change (Δ T_ad) for La(Fe, Si)₁₃-based stoichiometric compounds. Very recently, an off-stoichiometric composition LaFe_8.8Si_2.2 was reported, which has a single 1:13 phase directly formed in a solidification state, but shows a rather low value of Δ S (about 2 J/kg· K in 1.5 T).^[16] In this paper, we present a new La-rich composition of La_1.7Fe_11.6Si_1.4. Large Δ S of about 18 J/kg· K in 2 T in this alloy and its hydride was obtained. A peculiar microstructure and corresponding first-order magnetostructural transition, and hydrogenation behavior are investigated.

An ingot with the nominal composition of La_1.7Fe_11.6Si_1.4 was prepared by induction melting in an argon atmosphere. As-cast alloys were annealed at 1323 K for different times from 1 to 7 days in a quartz ampoule filled with argon, and then quenched into ice water. Hydrogenation was performed in a furnace filled with 2 atm H₂ atmosphere at 473 K for 5 hours to saturate H concentration.^[17] The H concentration was determined by hot extraction method (ONH, TCH-600). The crystal structure was studied using a powder x-ray diffraction (XRD, Bruker D8, Cu-K_α radiation). The microstructure was observed by scanning electron microscope (SEM, FEI Quanta 250 FEG). The phase composition was analyzed by electron microprobe (EM, JXA-8100), which has a high accuracy about ± 0.1 wt.%. Magnetic measurements were carried out using a Quantum Design MPMS SQUID vibrating sample magnetometer.

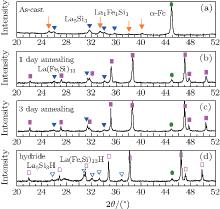
Apart from usually observed α -Fe and 1:1:1 phases in stoichiometric La(Fe, Si)₁₃ compositions, an additional phase in La_1.7Fe_11.6Si_1.4 was found by XRD presented in Fig. 1(a), which can be well indexed to be the La₅Si₃ phase (tetragonal, I4/mcm, a = 0.788 nm, c = 1.437 nm). Still, the α -Fe is the main phase in the as-cast sample. The phase constitution dramatically changed upon a short-time annealing for 1 day, as shown in the XRD pattern in Fig. 1(b). The phase constitution was almost unchanged upon annealing for 3 days as shown in the XRD pattern in Fig. 1(c). Full hydrogenation shifts all XRD peaks to lower angles excepted for the α -Fe phase, indicating that the values of lattice constant a increase from 1.142 nm to 1.155 nm for 1:13 phase, and for La₅Si₃ phase the values of lattice constant a and c increase from 0.788 nm to 0.798 nm and 1.437 nm to 1.483 nm respectively, as shown in Fig. 1(d). Figures 2(a)– 2(c) shows the microstructure of the specimens annealed at 1323 K for 0– 3 days. The as-cast sample contains the α -Fe (black phase), 1:1:1 phase (gray phase) and La₅Si₃ phase (white phase). From the SEM observation in Figs. 2(b) and 2(c), the 1:13 grains exhibiting a faceted morphology are surrounded by La₅Si₃. The volume fraction of the 1:13 phase nearly reaches 80%, whereas the La₅Si₃ phase was retained, but there observed little amount of α -Fe and no 1:1:1 phase. A prolonged annealing up to 7 days did not impact this microstructure very much (not shown here). According to the previously established La– Fe– Si ternary phase diagram, ^[18] the La₅Si₃ phase locates at the La rich boundary. The formation of this Si-rich and Fe-free La₅Si₃ phase is expected to result in the 1:13 matrix being depleted of Si, thus the concentration of Fe increases in the 1:13 matrix and the MCE is enhanced.^[5] This assumption was confirmed by the result of electron microprobe, which suggests the real composition of the 1:13 matrix as La_8.18Fe_83.59Si_8.24 ( = La_1.16Fe_11.83Si_1.17). As the La(Fe, Si)₁₃ compound with a lower Si content has a higher capability to absorb hydrogen due to a large weighted average Fe– Fe distance, ^[19] it seems reasonable that the present 1:13 hydride matrix contains high H content. The amount of H in this sample is measured to be 3100 ppm. This value is much higher than that in La_1.0Fe_11.8Si_1.2(∼ 2320 ppm).^[19] However, we are not able to exclude the H in the secondary phase La₅Si₃ without knowing its hydrogen absorption capability. Interestingly, hydrogen decrepitation process leads to single crystalline particles by almost keeping the initial shape and size of the non-hydrogenated 1:13 grains, as shown in Fig. 2(d). Also, some residual La₅Si₃ and α -Fe phases adhesive on fracture surfaces are visible. The form of single crystalline La– Fe– Si particles would seem more attractive for magnetic refrigerant applications.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. XRD patterns of as-cast, annealed, and hydrogenated La1.7Fe11.6Si1.4.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. SEM backscattered electron images of as-cast bulk La1.7Fe11.6Si1.4 (a), annealed for 1 day (b) and 3 day (c) at 1323 K. (d) Single crystalline hydride particle.

It has been known that in order to exploit the potential of Δ T_ad in a finite field for first-order transition materials, a sharp magnetostructural transition is desirable, and more importantly the field dependence of transition temperature (dT_c/dH) has to be optimized.^{[3, 20, 21]} The optimal value of dT_c/dH for Ni_49.8Mn₃₅In_15.2 is 7.8 K/T, ^[3] and 6.5 K/T for La(Fe, Si)₁₃system.^[20] From the magnetization versus temperature at different fields (0.2 and 1 T) in Fig. 3, the value of dT_c/dH for La_1.7Fe_11.6Si_1.4 is calculated to be 6.3 K/T that is very close to the theoretical optimized one suggested by Sandeman.^[20] This ideal case would give rise to the maximum Δ T_ad of 13 K.^[20] A large Δ T_ad of 5.5 K in 2 T has been found by the direct experimental measurement for La_1.7Fe_11.6Si_1.4 (not shown here), but still far from the theoretical value. This discrepancy implies that a higher driven field is required to reach the upper bound of cooling effect. Nevertheless, the large dT_c/dH and steep transition in first order transitions are favorable for the table-like temperature dependence of MCE, as reported in antiperovskite Mn₃GaC alloys.^{[22, 23]} In comparison, stoichiometric composition La_1.0Fe_11.6Si_1.4 shows a smaller value of dT_c/dH about 3.6 K/T and slightly smeared magnetostructural transition at high fields.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Comparison of magnetization as a function of temperature on applying different field in La1.7Fe11.6Si1.4 and La1.0Fe11.6Si1.4. The insert shows the shift of transition temperature by increasing magnetic field.

Figure 4 shows the isotherms and related magnetic entropy change as a function of temperature and field for La_1.7Fe_11.6Si_1.4 annealed for 3 days and its hydride La_1.7Fe_11.6Si_1.4H_2.9. For La_1.7Fe_11.6Si_1.4, the magnetization curves at temperatures well above T_c (173 K) show very small low-field susceptibility due to a little amount of α -Fe phase. A sharp change in magnetization above T_c from 184 K to 175 K takes place at a critical field. Combined the well-defined onset field with the observed large magnetic hysteresis width (∼ 1 T), this compound undergoes a typical first-order magnetostructural transition.^[24] The entropy change Δ S is calculated by using the Maxwell relation , where μ ₀ and H are permeability and magnetic field, respectively. The maximum Δ S value is 18 J/kg· K when applying a field of 2 T. An interesting feature is that the Δ S peak broadens asymmetrically toward higher temperature with increasing field, which can be ascribed to the field-induced itinerant electron metamagnetic transition.^[4] This characteristic causes a peculiar table-like Δ S curve over a wide temperature range of 10 K in 2 T, which is desirable for enhancement of the refrigerant capacity in an ideal Ericsson cycle magnetic refrigeration. In comparison, the temperature range for the Δ S plateau induced by 2 T field change has been reported to be 7 K in stoichiometric La_1.0Fe_11.9Si_1.1, and 2 K in La_1.0Fe_11.8Si_1.2.^[25] The full hydrogenated La_1.7Fe_11.6Si_1.4H_2.9 sample exhibits much smoother magnetization curves, and its hysteresis width is significantly reduced to 0.1 T. Hysteresis for a system includes two components: intrinsic hysteresis due to lattice incompatibility between the transforming phases and extrinsic hysteresis caused by microstructural features such as grain boundaries and secondary phases.^[26] It is assumed that the current hydrogenation brings about the single crystalline 1:13 powders, and very likely removes grain boundaries as well as phase boundaries with the La₅Si₃ phase. Most importantly, the hydrogenation decrepitation does not impair the MCE. The Δ S still keeps a high level of 17 J/kg· K in 2 T. Moreover, a relatively lower field (e.g., 1 T, which can be more easily generated with Nd– Fe– B permanent magnets) can induce a large Δ S of 14 J/kg· K. The MCE is more pronounced than that observed in stoichiometric La_1.0Fe_{11.74− y}Mn_ySi_1.26H_1.53 (about 12 J/kg· K in 1.6 T), ^[27] indicating that the H distributes more homogeneously in La_1.7Fe_11.6Si_1.4H_2.9. We believe that the present novel microstructure exhibiting the 1:13 grains surrounded by the La₅Si₃ phase is helpful for hydrogen absorption. The magnetic field dependence of Δ S in samples before and after hydrogenation is also shown in Fig. 4. In the case of non-hydrogenated sample, the Δ S remains constant at low field, rapidly increases in a linear manner at a critical field, then saturates at higher field. This discontinuity becomes smeared in hydrogenated sample, which can be interpreted by the disappearance of Δ S plateau.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (a), (b) Magnetization versus field at various temperatures, (c), (d) entropy change versus temperature at various fields, and (e), (f) entropy versus field at various temperatures, for non-hydrogenated (left column) and hydrogenated La1.7Fe11.6Si1.4 (right column).

Last, we compare the influence of hydrogenation on the T_c and MCE between La_1.7Fe_11.6Si_1.4 and La_1.0Fe_11.6Si_1.4, as shown in Fig. 5. One aspect is that the decrease of the Δ S upon hydrogenation in La_1.0Fe_11.6Si_1.4 is about 20% (the data taken from Ref. [15]), whereas it keeps constant in La-rich sample. On the other hand, the T_c of La_1.7Fe_11.6Si_1.4 is lower than that of La_1.0Fe_11.6Si_1.4, but hydrogen shifts T_c of La_1.7Fe_11.6Si_1.4 to a higher value exceeding that in La_1.0Fe_11.6Si_1.4. This phenomenon has been explained by the different space for H in the unit cell.^[20] From this result, it can be concluded that the 1:13 matrix phase of La_1.7Fe_11.6Si_1.4 should contain more H than the single 1:13 phase in La_1.0Fe_11.6Si_1.4 (about 2041 ppm), although the La₅Si₃H_y phase also contributes H concentration to the sum H amount.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Temperature dependence of entropy change for 2 T field change in La1.7Fe11.6Si1.4 and La1.0Fe11.6Si1.4 and their hydrides.

We have reported a new off-stoichiometric La_1.7Fe_11.6Si_1.4. The dual-phase structure with 1:13 (80 vol.%) and La₅Si₃ phases can be obtained by only 1 day annealing. This novel composition exhibits table-like large entropy change. Hydrogenation results in the single crystalline 1:13 particles with size of 60– 80 μ m. The hydride particles contain high H concentration and high T_c, and exhibit large Δ S of 14 J/kg· K in 1 T accompanying with small hysteresis losses. These features suggest that the present La-rich alloy is a highly suitable refrigerant candidate for magnetic refrigerators.