Surface plasmon polaritons (SPPs) are slow waves that are caused by the collective oscillations of the free electron gas in noble metals.^{[1, 2]} They can be excited not only by plane waves with wave vector compensation, but also by perpendicularly or parallelly moving electron beams (e-beam).^{[3– 7]} SPPs have become attractive research topics due to their interesting physics and important applications, such as enhanced radiation, ^{[8– 10]} enhanced optical transmission, ^[11] field imaging, ^[12] terahertz devices, ^[13] and biosensor.^[14]

Recently, an attractive SPPs Cherenkov light radiation source (SPCLS) with a simple structure of a metal film with a dielectric medium loading was presented in Ref.  [8]. In SPCLS, SPPs on the metal film are at first excited by a parallelly moving e-beam. They are then transformed into radiation waves with strong power enhancement when the Cherenkov radiation (CR) condition is satisfied in the dielectric medium. SPCLS provides a promising way to obtain a coherent and tunable radiation source within a wide frequency range or a sensitive particle detector.^[15] SPCLS can also be excited by a perpendicularly moving e-beam. However, the radiation waves in this case are incoherent and untunable because all of the SPPs are excited by the perpendicularly moving e-beam.^[7] In this paper, we aim to look for stronger radiation power enhancement and extend the radiation frequency tuning band by analyzing the physical process of the radiation transformation in parallelly excited SPCLS and investigating their radiation properties.

This paper is organized as follows. The physical process of the radiation transformation in SPCLS is analyzed in Section 2. The dependencies of the radiation power enhancement on the e-beam energy and the film thickness are presented in Section 3. Section 4 analyses the radiation frequency. Section 5 gives the summary.

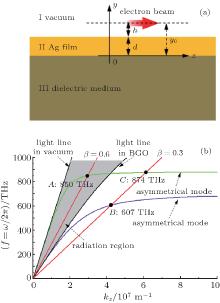
A schematic of SPCLS is shown in Fig.  1(a), in which a metal film is supported by a dielectric medium and an e-beam is uniformly moving parallel to the metal film surface. 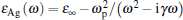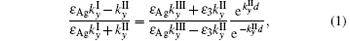Many materials, such as metals Ag, Au, Al and dielectric media Bi₃Ge₄O₁₂ (BGO), SiC, SiO₂, ZnSe, MgO-TiO₂, can be used in SPCLS.^[8] To simplify the analysis, in this paper the dielectric medium is BGO, ^[16] and the metal film is Ag with its relative permittivity described by the modified Drude model , where ε _∞ = 5.3, ω _p = 1.39 × 10¹⁶  rad/s, and γ = 3.21 × 10¹³  Hz.^{[17– 20]} Making use of the Maxwell’ s equations and the boundary conditions, we can obtain the dispersion equation of SPCLS

where , k₀ = ω /c, c is the velocity of light in a vacuum, and ε _Ag and ε ₃ are the relative permittivities of the Ag film and BGO, respectively. The dispersion curve is drawn in Fig.  1(b).

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. (a) Schematic of SPCLS: Ag film is supported by dielectric medium Bi3Ge4O12 (BGO). (b) Dispersion curve of SPCLS: film thickness d = 50  nm, the medium is BGO. The shaded part between the light lines in vacuum and in the medium is the radiation region.

For the thin metal film supported by a dielectric medium, there are symmetrical and asymmetrical modes of SPPs, depending on the distribution of field E_z on the perpendicular direction of the film (Y direction in this structure).^[1] As shown in Fig.  1(b), the dispersion curves of both modes are always below the light line in vacuum because SPPs are slow waves and none of them can be transformed into radiation waves in the vacuum. However, the wavevector of part of the asymmetrical mode can be smaller than that of light in the dielectric medium. Then, as shown in Fig.  1(b), part of its dispersion curve locates in the radiation region between the light lines in a vacuum and those in the dielectric medium. SPPs located in this region can be transformed into radiation waves. When SPCLS is excited by a parallel e-beam, only the SPPs corresponding to the working point, which is the cross point of the e-beam line and the dispersion curve, can be excited.^[7] This means that if the working point lies in the radiation region, then coherent radiation waves can be obtained in the dielectric medium.

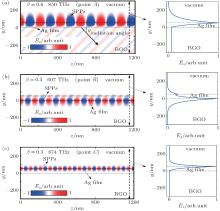
For example, in the case of e-beam energy β = 0.6 (the e-beam energy is described by β , where β = u₀/c and u₀ is the velocity of the moving e-beam), the corresponding working point A lies in the radiation region, and then the excited SPPs with operating frequency 850  THz can be transformed into radiation waves, whose contour map is shown in Fig.  2(a). It is illustrated in this figure that the excited SPPs are confined to the vacuum/film interface and they decay exponentially away from this interface in the vacuum. In the film, the excited SPPs decay rapidly in the Y direction until they are transformed into radiation waves in the medium. This indicates that the SPPs are excited firstly on the vacuum/film interface by the parallelly moving e-beam, and they then penetrate though the metal film with attenuation along the Y direction. Finally, they are transformed into radiation waves in the dielectric medium with a radiation angle that is determined by the e-beam energy together with the permittivity of the dielectric medium, as shown by the following equation:

Accordingly, the radiation angle can be changed by adjusting the e-beam energy, and the maximum radiation angle θ _max is determined by the dielectric medium.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Contour maps of the excited SPPs, the thickness of the film is 50  nm, and the dielectric medium is BGO: (a) contour map of Ez at 850  THz for β = 0.6 (asymmetrical mode); (b) contour map of Ez at 607  THz for β = 0.3 (symmetrical mode); (c) contour map of Ez at 874  THz for β = 0.3 (asymmetrical mode).

In the case of β = 0.3, the corresponding working points B and C lie outside of the radiation region, the excited SPPs with operating frequencies 607  THz and 874  THz cannot be transformed into radiation waves, whose contour maps are show in Figs.  2(b) and 2(c), respectively. It can be seen that the fields of the excited SPPs are both confined to the film surface and decay exponentially to zero along the Y direction. The skin depths of the SPPs fields in vacuum and dielectric are and , respectively, where and are given in Eq.  (1).

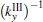
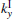
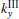
In the case that an e-beam is moving parallel to a dielectric medium without a metal film, CR can be generated in the medium when the e-beam energy is larger than the CR threshold.^{[8, 21, 22]} When there is a metal film located above the dielectric medium (SPCLS), due to the excited SPPs in the film, the radiation power (P_SPCLS) can be enhanced compared to that without the metal film (P_CR). This enhancement can then be obtained in the frequency domain by η (ω ) = P_SPCLS/P_CR.

3.1. Power intensity ratio and SPPs’ energy loss

To analyze the radiation power enhancement in SPCLS, we first study the power intensity ratios on the vacuum/film interface of the excited SPPs and the incident waves from e-beam at the SPPs’ operating frequency. Making use of the nonhomogeneous Helmholtz equation and the boundary conditions, we can obtain the electric field of the excited SPPs on the vacuum/film interface of SPCLS:

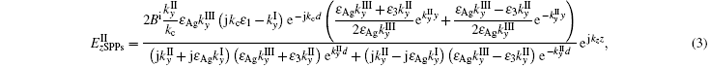
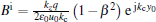
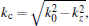
where , q is the charge density of the e-beam, and k_z = ω /u₀.

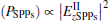
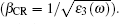
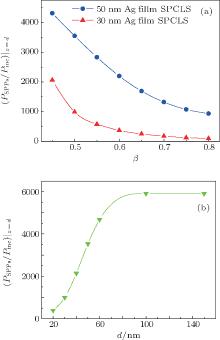
Based on the relationship , the power intensity P_SPPs| _{z= d} (d is the film thickness as shown in Fig.  1(a)) of the excited SPPs on the vacuum/film interface can be obtained, as can that of the incident waves P_inc| _{z= d}.^[23] The power intensity ratios of the excited SPPs and the incident waves at the SPPs’ operating frequency for varying e-beam energy in SPCLS with 30  nm and 50  nm Ag films are shown in Fig.  3(a). In this paper, we focus on the excited SPPs that can be transformed into radiation waves, and then the e-beam energy should be larger than the CR threshold β _CR It can be seen that this ratio decreases with the increasing e-beam energy, and the largest value is obtained at the e-beam energy near to β _CR in BGO. For example, excited by an e-beam of β = 0.45 (61  keV), the SPPs obtain the power intensity ratio 2063 in SPCLS with 30  nm Ag film and 4314 with 50  nm Ag film.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. The power intensity ratios on the vacuum/film interface of the excited SPPs and the incident waves from e-beam at the SPPs’ operating frequency: (a) dependencies of the power intensity ratio on e-beam energy for SPCLS with 30  nm and 50  nm Ag films; (b) dependence of the power intensity ratio on Ag film thickness for fixed e-beam energy β = 0.5.

The dependence of this ratio on the film thickness for fixed e-beam energy β = 0.6 is shown in Fig.  3(b). It can be seen that the power intensity ratio at first increases to a peak value with the increasing film thickness, it then saturates. This happens because when the film is thick enough, thicker than 80 nm as shown in Fig.  3(b), the excitation of SPPs on the film can be regarded as that on a semi-infinite metal.^[7]

In SPCLS, the excited SPPs on the vacuum/film interface penetrate though the film with rapid attenuation along the Y direction. They are then transformed into radiation waves on the film/medium interface. Accordingly, the energy loss of the excited SPPs in the film should also be studied to analyze the radiation power enhancement in SPCLS. For the Ag film in SPCLS with fixed thickness, the SPPs’ energy loss decreases with the increasing e-beam energy. This happens because the propagation constant k_z (k_z = ω /u₀) of the excited SPPs in Eq.  (2) decreases with the increasing e-beam energy. The decreasing k_z leads the decreasing wave number 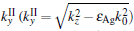along the Y direction. This leads to the increase of the skin depth of the excited SPPs field, which is inversely proportional to the penetration energy loss for the Ag film with fixed thickness. On the other hand, for the fixed e-beam energy, the energy loss increases with the increasing film thickness. This happens because the increasing film thickness gives rise to the increasing distance of attenuation of the excited SPPs.

3.2. Radiation power enhancement in SPCLS

Based on the physical process of the radiation transformation in SPCLS, the radiation power enhancement is determined by the power intensity ratio of the excited SPPs and the incident waves from e-beam, together with the SPPs’ penetration energy loss in the film. We now use the results given above to analyze the dependencies of the radiation power enhancement on the e-beam energy and parameters of the film.

The radiation field in the dielectric medium can be obtained as

where Bⁱ and k_c are the same as those given in Eq.  (3). When the e-beam energy is larger than β _CR in the dielectric medium, in Eq.  (4) is imaginary, and then becomes a radiation field. Based on the relationship , the radiation power P_SPCLS can be calculated, and then the radiation power enhancements η (ω ) can be obtained, which are illustrated in Figs.  4(a) and 4(b).

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Radiation power enhancement of SPCLS at the operating frequency: (a) dependence of the enhancement on e-beam energy for SPCLS with 30  nm Ag film; (b) dependence of the enhancement on e-beam energy for SPCLS with 50  nm Ag film. The insets show the enhancement of all of the frequency components in SPCLS.

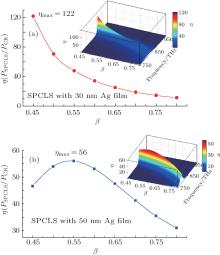
As shown in Fig.  4(a), for SPCLS with 30  nm Ag film, the radiation power enhancement η decreases rapidly with the increasing e-beam energy. It obtains the maximum value η _max = 122 when the e-beam energy (β = 0.45) is near to β _CR in BGO. This happens because the penetration energy loss of the excited SPPs is very weak for the 30  nm Ag film, and the power intensity of the excited SPPs dominates the radiation power enhancement in SPCLS. The power intensity of the excited SPPs decreases with the increasing e-beam energy, and this causes the decreasing enhancement in SPCLS.

However, the dependence of this enhancement on the e-beam energy exhibits a different tendency for SPCLS with 50  nm Ag film. As shown in Fig.  4(b), the enhancement at first grows with the increasing e-beam energy, it then decreases. The maximum value η _max is 56 at e-beam energy β = 0.54 (96  keV). This happens because the penetration energy loss of the SPPs becomes remarkable for the 50  nm Ag film, and then the enhancement is determined by the power intensity of the excited SPPs together with their penetration energy loss. When the e-beam energy is near to β _CR, the energy loss dominates this enhancement in SPCLS. The energy loss decreases with the increasing e-beam energy, which causes the increasing enhancement. With a further increase of the e-beam energy, the decreasing power intensity of the excited SPPs determines the enhancement in SPCLS, which causes the decreasing enhancement. It can be clearly seen from the insets of Figs.  4(a) and 4(b) that for radiation waves in SPCLS only the frequency component at the operating frequency of the excited SPPs is dramatically enhanced.

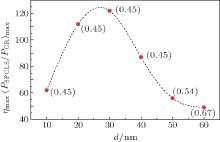
The dependence of the maximum radiation power enhancement η _max (at the optimized e-beam energies) in SPCLS on varying Ag film thickness is shown in Fig.  5. It can be seen that the maximum enhancement increases with the increasing film thickness from 10  nm to 30  nm and then decreases, and η _max obtains the largest value when the Ag film thickness is between 20  nm and 30  nm. When the film is 10  nm or 20  nm thick, the power intensity of the excited SPPs is very small, which in turn leads to a small η _max. With the increase of the film thickness, not only the intensity of the excited SPPs but also the energy loss in the film increases. When the film thickness is larger than 30  nm, the large energy loss also leads to a small η _max. Accordingly, the largest value of η _max can be obtained by optimizing the thickness of the Ag film in SPCLS together with the e-beam energy.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. The dependence of the maximum power enhancement at the optimized e-beam energy on the film thickness, the optimized e-beam energies are also labeled in the figure. The dielectric medium is BGO.

Because the radiation frequency of SPCLS is determined by the operating frequency of the excited SPPs, it can be tuned by adjusting the e-beam energy. The dispersion curves of SPCLS with 30  nm Ag film and 50  nm Ag film in the radiation region are shown in Fig.  6(a). It can be seen that, for SPCLS with 30  nm Ag film, the radiation frequency is 875  THz for β = 0.45, and 843  THz for β = 0.75. Whereas for SPCLS with 50  nm Ag film, it is 866  THz for β = 0.45, and 812  THz for β = 0.75. Accordingly, in the same e-beam energy variation range, a wider radiation frequency tuning band can be obtained in SPCLS with 50  nm Ag film against that with 30  nm Ag film. As shown in Fig.  6(b), the tuning band of radiation frequency of SPCLS with 50  nm Ag film reaches up to 6.5% (β from 0.45 to 0.75), whereas that of SPCLS with 30  nm Ag film is 3.6% (β from 0.45 to 0.75).

Fig.  6.

	Figure Option ViewDownloadNew Window
	Fig.  6. (a) The dispersion curves in the radiation region for SPCLS with 50  nm Ag film and 30  nm Ag film. (b) The dependencies of the radiation frequencies on the e-beam energy.

Since the dispersion relation of asymmetrical mode of SPPs is mainly determined by the SPPs on the vacuum/film interface, the permittivity of the dielectric medium almost makes no differences to the radiation frequency of SPCLS when the radiation is generated. The radiation frequency then remains almost the same with the increasing permittivity of the dielectric medium, but the radiation angle will increase with the increasing permittivity.

The detailed analyses and numerical calculation given in this paper show that, in SPCLS, SPPs are first excited by the parallel moving e-beam on the vacuum/film interface and then penetrate though the metal film until they are transformed into enhanced and coherent radiation waves in the dielectric medium. Strong radiation power enhancement and wide radiation frequency tuning band in SPCLS can be obtained by optimizing the e-beam energy and the film thickness. For SPCLS with Ag film and BGO medium, the largest radiation power enhancement reaches up to 122 times and the radiation frequency tuning band reaches up to 6.5%. The results obtained in this paper will facilitate the practical applications of light radiation source and the sensitive particle detector of SPCLS.