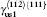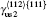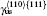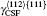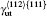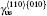†Corresponding author. E-mail: xiaozhiwu@cqu.edu.cn
‡Corresponding author. E-mail: qingliu@cqu.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 11104361 and 11304403) and the Fundamental Research Funds for the Central Universities, China (Grant Nos. CQDXWL2014003 and CDJZR14328801).
Using first principles calculations combined with the quasiharmonic approach, we study the effects of temperature on the elastic constants, generalized stacking fault energies, and generalized planar fault energies of Ni3Al. The antiphase boundary energies, complex stacking fault energies, superlattice intrinsic stacking fault energies, and twinning energies decrease slightly with temperature. Temperature dependent anomalous yield stress of Ni3Al is predicted by the energy-based criterion based on elastic anisotropy and antiphase boundary energies. It is found that p increases with temperature and this can give a more accurate description of the anomalous yield stress in Ni3Al. Furthermore, the predicted twinnablity of Ni3Al is also decreasing with temperature.
The L12 ordered alloy Ni3Al is widely used as high temperature structural material because of their superior mechanical properties, such as high strength and resistance to creep.[1– 5] The temperature dependent anomalous yield stress, the rise of yield strength with temperature increasing, is observed in Ni3Al intermetallics.[6, 7] This phenomenon has attracted much attention due to the high temperature applications.[8, 9] It has been generally accepted that anomalous yield stress is an intrinsic property originated in the structure and properties of superdislocations, and is due to thermally activated cross slip from the (111) primary slip plane to the (010) cross slip plane. The difference in antiphase boundary (APB) energy on (111) and (010) planes is one of the key factors controlling the activation enthalpy of cross slip of a ⟨ 110⟩ (111) dislocation.[10, 11] The anomalies results from the type-I dissociation of 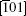
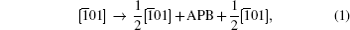
where 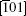
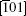

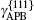

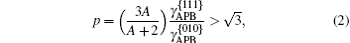
with A = 2C44/(C11− C12) the elastic anisotropy ratio. The transition from anomalous to normal temperature dependence of yield strength of (Ni1− xFex)3Ge has been investigated by Liu et al. based on the fact that Ni3Ge exhibits an anomaly while Fe3Ge does not.[13] The impacts of 5d transition metals Re and Pt on yield stress anomaly of Ni3Al are predicted by the APB anisotropy ratio.[14] Tichy et al. suggested that the anomaly is also controlled by type-II dissociation of 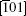

where 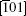

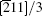
Deformation twinning is another deformation mechanism for plastic deformation in Ni3Al. The twinning mechanism plays an important role in Ni3Al with a limited number of independent slip systems, and deformation twinning has been reported by many researchers under various creep loading conditions.[25– 27] For example, Viswanathan et al.[28] employed the diffraction contrast and high-resolution TEM to investigate the deformation mechanisms during intermediate temperature creep of Ni-based superalloys, and found that microtwinning occurs via sequential movement of identical 1/6⟨ 112⟩ Shockley partials on successive (111) planes. Xie et al.[29] used the molecular dynamics (MD) simulation to explore the dislocation formation and twinning from the crack tip in Ni3Al. It is well known that the generalized planar fault (GPF) energy curve can predict the preference for twinning in fcc metals and alloys. Recently, there have been many theoretical studies focused on the qualitative dependence of mechanical twinning tendency (twinnability) on the GPF energy curve in fcc metals and alloys.[30– 40] The entire GPF energy curve along the pseudo-twinning direction of 1/6⟨ 112⟩ (111) in L12 structure alloys has been determined using ab intio calculations.[41, 42] However, the entire GPF energy curves along the pseudo-twinning direction at different temperatures and, in particular, the temperature dependence of the twinnability, have not yet been reported for Ni3Al alloy.
In this paper, we employ the first principles methods and quasiharmonic approximation to investigate the GSF energy and GPF energy curves at different temperatures. The main focus is the effects of temperature on elastic constants, anisotropy, APB energies and twinning energies. Based on the above results, temperature dependent yield strength anomaly and twinnability of Ni3Al are also discussed.
The Helmholtz free energy of Ni3Al at a constant volume V and T has three major contributions[43, 44]

where E0(V) is the 0 K total energy and Fel is the thermal electronic contribution to free energy from finite temperature via integration over the electronic density of state (DOS) following the Fermi– Dirac distribution.[45, 46] Both the E0(V) and Fel can be obtained from first principles calculations. Fvib is the phonon free energy arising from the lattice vibrations. The phonon free energy within the framework of a quasiharmonic approach can be expressed as
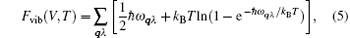
where ω qλ represents the frequency of the λ -th phonon mode at wave vector q, and the sum is over all wave vectors q and over all three phonon branches λ in the first Brillouin zone.
The isothermal elastic constants are defined as the second derivatives of the Helmholtz free energy with respect to strain
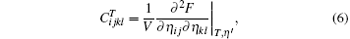
where η ′ indicates that all other strains are held fixed and V = V(T) is the equilibrium volume at temperature T. There are three independent elastic constants 
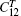

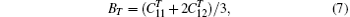
and determined from the Vinet equation of state[47] corresponding to a pure volume deformation of the lattice. We apply a volume-conserving orthorhombic strain to calculate the difference between 
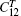
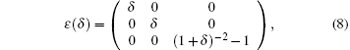
and the corresponding free energy change is
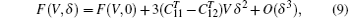
with F(V, 0) as the free energy of the unstrained structure.
We use a volume-conserving tetragonal strain to determine 
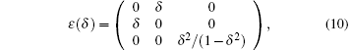
which leads to the energy change
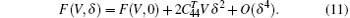
In this paper, we use the quasistatic approach proposed by Wang et al.[48, 49] to calculate the temperature dependence of elastic constants of Ni3Al. It is based on the assumption that the temperature dependence of elastic constants is solely caused by thermal expansion. There are abundant experimental evidences[50– 52] which support the approximation. The quasistatic approach has the following three steps.[48] The first step is calculating the equilibrium volume V(T) at given T using the first-principles quasiharmonic approximation. In the second step, based on the energy-strain relations Eqs. (8)– (11), we predict that the static elastic constants at 0 K as a function of volume 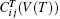
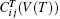

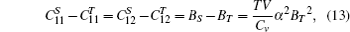
where CV is the isochoric heat capacity and α is the thermal expansion coefficient.
The calculations reported in this work are performed with the Vienna ab initio Simulations Package (VASP) code.[53] The electron– ion interactions are described by the projector augmented wave (PAW) method[54] and the exchange-correlation functionals are treated by the generalized gradient approximation (GGA) of Perdew– Burke– Ernzerhof (PBE).[55] Convergency of the total energies with respect to the number of k-point meshes and the energy cut-off has been checked. Here, the wave functions are sampled on 21× 21× 21 k-point mesh for elastic constants calculations and 21× 21× 1 for GSF energies and GPF energies calculations based on the Monkhorst– Pack scheme[56] together with the linear tetrahedron method incorporating Blö chl corrections.[57] The energy cut-off of plane wave is set to 500 eV for all calculations. The total energy is converged numerically to less than 10− 6 eV per atom with respect to electronic self-consistency. We adopt a 48-atom supercell consisting of 10 (111) atomic planes to calculate fault energies to generate GSF energy and GPF energy curves at different temperatures. Between the periodically repeated supercell a vacuum layer with a thickness of 7 (111) atomic planes is added to avoid the fault energy interaction in adjacent cells due to periodic boundary conditions. Due to the ferromagnetic nature of Ni-containing materials, all the calculations are performed within the spin polarization approximation.
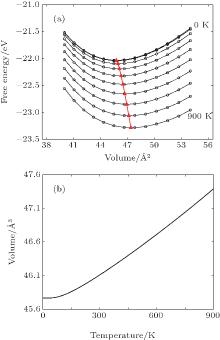
Phonon calculations are carried out by the supercell approach as implemented in the PHONOPY package, [58– 60] with VASP again the computational engine. The chosen supercell size strongly influences on the thermal properties. Therefore, the adequate supercell size consisting of 3× 3× 3 unit cells with 108 atoms is chosen to calculate the phonon frequency in Ni3Al. The forces resulting from displacements of certain atoms in the supercell are calculated by the VASP code with 7× 7× 7 k-point mesh for BZ integrations. The other settings of VASP calculations are the same as those described above. The phonon modes are obtained by using the PHONOPY, which can support the VASP interface to calculate force constants directly in the framework of density-functional perturbation theory (DFPT).[61] Additional details of phonon methodology can be found in Refs. [62] and [63]. Figure 1 represents the calculated phonon dispersion curves for Ni3Al along several high-symmetry directions in the Brillouin zone together with the room temperature measurements by neutron diffractions of Ni3Al.[64] A good agreement is observed between calculations and measurements. The method to calculate the temperature dependent lattice constants for Ni3Al is the same as our calculations for Al, Ni, and Cu.[62, 62] Figure 2(a) represents the free energy as a function of unit cell volume of Ni3Al at every 100 K between 0 and 900 K and the values depicted by the red triangle-up is the equilibrium volume at the corresponding temperature. Obviously, the thermal expansion is obvious as the equilibrium volume is increasing (see Fig. 2(b)).
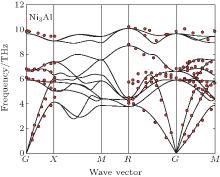 | Fig. 1. Phonon spectrum of the intermetallic compound Ni3Al. The calculated values are plotted as solid lines and those from the inelastic neutron scattering measurement[64] are plotted as red solid circles. |
The temperature dependence of elastic constants is important for predicting and understanding the mechanical strength, stability, and phase transitions of a material.[65] In this work, we employ the first-principles quasistatic approach[48, 49] to determine the temperature dependent elastic constants of Ni3Al. The calculated equilibrium lattice constant and elastic constants at T = 0 K in comparison with previous theoretical results[66– 74] and experimental values[75, 76] are tabulated in Table 1. In general, our results are in good agreement with experiments and previous theoretical calculations. Figure 3(a) shows the calculated adiabatic elastic constants in comparison with experimental data from rectangular parallelepiped resonance measurements by Tanaka and Koiwa[77] and Prikhodko.[78] The calculated 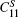
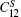
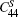
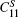
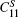
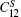
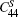
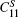
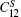
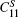
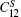
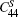
 | Fig. 3. (a) The calculated adiabatic elastic constants (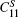 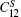 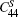 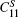 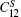 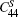 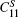 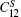 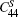 |
Table 1. Calculated equilibrium lattice constant a (Å ) and elastic constants Cij (GPa) for Ni3Al at 0 K compared with previous computed results and experimental data. Note that 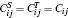 |
As is well known, cubic crystals have elastic anisotropy as a result of the fourth rank tensor property of elasticity. The present results for 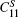
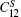
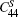

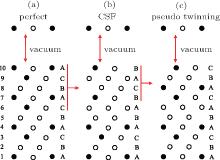
The plastic behavior of Ni3Al is determined by the dislocation motion and deformation twinning. It is widely accepted that three different types of dislocation dissociations exist in L12 Ni3Al. A stable dislocation dissociation is that a ⟨ 110⟩ superdislocation dissociates into two 1/2⟨ 110⟩ superpartials bound by APB either on the (111) or (010) plane, type-I dissociation in Eq. (1). Also, the 1/2⟨ 110⟩ (111) superpartial may further dissociate into two 1/6⟨ 112⟩ (111) Schockley partials separated by complex stacking fault (CSF) called a metastable dislocation dissociation, namely
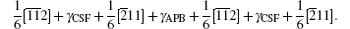
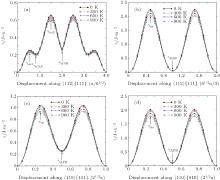
Another stable dislocation dissociation is that the ⟨ 110⟩ (111) dislocation will also dissociate into two 1/3⟨ 112⟩ (111) dislocations bound by superlattice intrinsic stacking fault (SISF), type-II dissociation in Eq. (2). In this paper, based on the lattice constant versus temperature relations a(T), all these GSF energy curves in the temperature range of 0– 900 K are calculated and plotted in Fig. 4. The change of GSF energies at elevated temperature are mainly caused by volume change due to thermal expansion. The quasiharmonic approach lets one take into account the anharmonicity of the potential at the first order: vibrational properties can be understood in terms of the excitation of the noninteracting phonon. Therefore, the quasiharmonic approximation is usually appropriate if the temperature is lower than the melting point. Therefore, we only calculate the GSF energy curves up to 900 K that is lower than the melting point.
The calculated APB energies, CSF energies, and SISF energies are illustrated in Table 2. Based on these results, we predicted the anomalous yield stress phenomenon by Eq. (2), the energy-based condition. Obviously, all the calculated p at different temperatures satisfy 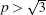
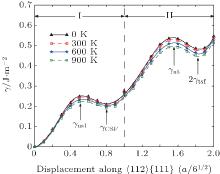
There are two types of deformation twining in Ni3Al. One deformation twinning called pseudo-twinning is formed via the sequential motions of identical 1/6⟨ 112⟩ Shockley partials and the other deformation twinning called anti-twinning is generated by sequential shear of 1/3⟨ 112⟩ dislocations on successive (111) planes. The GPF energies along the shear direction are evaluated on the two (111) planes. Figure 5 shows the temperature dependent GPF energies curves of Ni3Al. The first half of each GPF energy curve is evaluated by sliding the upper 6– 10 atomic layers relative to atomic layers 1– 5 over a distance 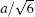
Previous study has shown that the relative sizes of γ us and γ ut can describe the ease with which an fcc material deforms by twinning relative to deforming by dislocation-mediated slip.[30] According to this analysis, once a leading partial dislocation has been nucleated, whether a subsequent nucleation event will consist of a trailing partial dislocation (i.e., a perfect dislocation) or of a second leading partial on an adjacent slip plane (micro-twin) will be determined by the difference 
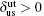

Table 2. Stacking fault energies (J/m2), relative barrier difference  |
A more thorough treatment of the balance between dislocation-mediated slip and deformation twinning has been proposed by Tadmor and Bernstein[31] in the following form:
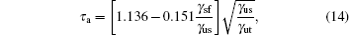
where γ sf and γ us are replaced by γ CSF and γ us1 for the pseudo-twinning in Ni3Al, respectively. τ a is a relative measure of the tendency of an fcc metal to undergo deformation twinning: a larger τ a indicates a greater propensity for twinning. So far, the temperature dependence of the twinnability of Ni3Al along the pseudo-twinning direction has not been calculated. The computed values of τ a based on Eq. (14) for Ni3Al are listed in Table 2. It can be seen that the twinnability parameter of Ni3Al at 0 K is smaller than those of the fcc pure metals, such as Al (τ a = 0.930), Cu (τ a = 1.001), and Ag (τ a = 1.042).[31] Further, the twinnability of Ni3Al at different temperatures is much smaller than those of fcc metals.[62] However, the twinnability is similar to that of TiAl (τ a = 0.776) along its pseudo-twinning direction.[37] From Table 2, it is easy to see that the twinnability of Ni3Al decreases with the increase of temperature, which has the same change trend with fcc metals.[62, 63] However, the twinnability of Ni3Al with temperature predicted by τ a and 

It is generally admitted that the change of charge density intrinsically determines the change of stacking fault energy. Here, the charge density differences on the fifth (010) and (111) planes of faulted and perfect structures are calculated in order to reveal the effect of temperature on the stacking fault energy of Ni3Al. As shown in Figs. 7(a)– 7(d), the significant charge density redistributions can be caused by shifting of the (010) plane at different temperatures. One can easily see that the charge density of 0 K is always larger than that of 900 K for perfect and APB structures. It demonstrates that Ni– Ni and Ni– Al interactions at 0 K are stronger than those at 900 K, all the total energies at 0 K are lower than those at 900 K. A similar charge density redistribution can occur by shifting of the (111) plane at different temperatures. Further, the relative charge density differences between the faulted structure and the perfect structure on the fifth (010) and (111) planes at different temperatures are plotted in Figs. 8(a)– 8(d), respectively. One can see that the relative charge density differences at 0 K on the (010) and (111) planes are slightly larger than 900 K, indicating that the fault energies of the (010) and (111) planes at 0 K are slightly higher than 900 K. In other words, the stacking fault energies decrease with temperature increasing.
In this paper, we employ first principles calculations combined with a quasiharmonic approach to study the effects of temperature on the elastic constants, GSF energies, and GPF energies of Ni3Al at different temperatures. The APB energies, CSF energies, SISF energies, and twinning energy decrease slightly with temperature. Temperature dependent anomalous yield stress of Ni3Al is predicted by the energy-based criterion based on elastic anisotropy and APB energies. It is found that p increases from 4.888 to 5.219 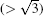
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|
| 51 |
|
| 52 |
|
| 53 |
|
| 54 |
|
| 55 |
|
| 56 |
|
| 57 |
|
| 58 |
|
| 59 |
|
| 60 |
|
| 61 |
|
| 62 |
|
| 63 |
|
| 64 |
|
| 65 |
|
| 66 |
|
| 67 |
|
| 68 |
|
| 69 |
|
| 70 |
|
| 71 |
|
| 72 |
|
| 73 |
|
| 74 |
|
| 75 |
|
| 76 |
|
| 77 |
|
| 78 |
|