It is widely believed that the strong electronic correlation is of key importance to high-T_c superconductors and determines the behavior of transition metal oxides.^[1] Up to now, the phase transition in strongly correlated electron systems is still the focus of interest in modern condensed matter physics. The minimal model that describes the essential physics of such systems is the one-band Hubbard model.^[2] This model on a one-dimensional (1D) lattice has been exactly solved.^[3] When the local interaction U is repulsive, the hall-filled 1D Hubbard model undergoes a metal– insulator transition (MIT) at U = 0 and the insulator is a Mott insulator with gapless spin and gapped charge excitations. This insulating state is incomprehensible within ordinary electron band theory and it is the result of strong electronic correlation. The Mott-type ground state has a characteristic spin-density-wave (SDW) with power-law decay of spin correlations.

Yet the Hubbard model is a homogeneous one with uniform repulsive interaction and on-site orbital energy. In consideration of the fact that real materials usually consist of several different kinds of atoms, some modified inhomogeneous Hubbard models are proposed. The ionic Hubbard model (IHM) with alternating potentials ± Δ at adjacent sites is regarded as a description to the neutral– ionic transition in mixed-stack organic charge-transfer salts^{[4, 5]} or the ferroelectric transition in perovskite oxides.^{[6, 7]} In 1D IHM, when U increases, the transition is from a band insulator to a Mott insulator, via a bond-ordered, ferroelectric insulator.^{[8– 15]} The Hubbard chains with special site-dependent potentials, such as the Fibonacci and Harper modulation, are also discussed.^[16] The alternating Hubbard model (AHM) with different U_A and U_B on neighbouring sites has been reported to simulate the systems whose spatial invariance is broken by two types of atoms, say “ anions” and “ cations” .^{[17, 18]} In the phase diagram of AHM, the system is always insulating and two types of regions, dominated by SDW and charge density wave (CDW), are observed.^[18] The generalized inhomogeneous model with site-dependent U has been also discussed.^[19] For considerable insight into the nonrandom inhomogeneous systems such as magnetic multilayer and superlattice, ^{[20– 23]} a 1D superlattice model with periodic arrangement of repulsive and free sites, but with constant orbital energy, has been widely studied for many different unit cell configurations and electron fillings.^{[24– 30]} The Mott– Hubbard insulator sets in at filling density ρ _I for these superlattice structures, ^[25] not at half-filling as in the Hubbard model. The period of SDW and the profile of local moment have rich properties.^[27] Here, we consider a more realistic superlattice model with the following Hamiltonian:

where i runs through all sites of the one-dimensional superlattice; is the creation (annihilation) operator for an electron with spin σ (↑ or ↓ ) at site i; and n_i = n_i↑ + n_i↓ are electron number operators. The hopping t is taken as the energy unit. The on-site Coulomb interaction U_i and the on-site potential ε _i are site-dependent. In the following discussion, we will treat the superlattices with L_U repulsive (U_i = U > 0, ε _i = ε ) sites and L₀ free (U_i = ε _i = 0) sites per unit cell.

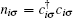
The electronic and magnetic properties of model (1) have been investigated by Lanczos diagonalization, ^[31] where the system size is typically less than 10. Some significant methodological studies imply that the properties of superlattice (1) are more sensitive to the modulation of ε than that of U.^{[32– 34]} In the previous work for L_U = L₀ = 1, ^[35] the system shows a correlated-metal phase at the particle– hole symmetrical point and becomes a band insulator beyond this point. The phase transition in superlattices with other combinations of L_U and L₀ has not been reported.

In this paper, we report charge and spin energy gaps and magnetic properties for superlattice Hamiltonian (1) at half-filling with the help of the density-matrix renormalization group (DMRG) procedure.^{[36– 40]} The unit cell of the superlattice here has L₀ = 1 to 6 free site(s) and L_U = 1 repulsive site. Section 2 presents the charge and spin excitations and the MIT of the Hubbard superlattice. In Section 3, magnetic properties, including local moment profile and SDW structure factor, are discussed. Section 4 gives the phase diagram and a summary.

The charge and spin excitation gaps Δ _C and Δ _S of the superlattices with N sites at half-filling can be given by

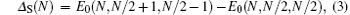
respectively. E₀(N_e, N_↑ , N_↓ ) is the ground state energy, N_σ (σ = ↑ or ↓ ) is the number of electrons with spin σ and thus the total number of electrons N_e = N_↑ + N_↓ and N_e = N at half-filling. To get the gaps in the thermodynamic limit (N → ∞ ), the finite-system DMRG algorithm is employed for chains with different lengths. We use a quadratic polynomial in 1/N to extrapolate the energy gaps under the thermodynamic limit^[35]

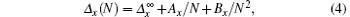
where x can be C (charge) or S (spin).

We start by examining the behaviors of energy gaps at the particle– hole symmetric point ε = − U/2. The finite-size behaviors of the spin and charge gaps for a superlattice with L₀ = 2 are shown in Figs. 1(a) and 1(b), respectively. For a definite chain length N, the spin gap Δ _S decreases with on-site repulsion U increasing. However, the extrapolation in Fig. 1(c) displays that as N → ∞ , Δ _S tends to be gapless regardless of the repulsion U (Δ _S for N → ∞ is also plotted in Fig. 1(a)). Nevertheless, with U increasing, the charge gap Δ _C in Fig. 1(b) hardly changes for small U. When U is large enough, Δ _C goes up rapidly. In the thermodynamic limit N → ∞ shown in Figs. 1(b) and 1(d), the charge gap Δ _C vanishes for small U and appears when U exceeds a critical U_c. Therefore, there is an MIT at U = U_c for the superlattice with L₀ = 2 and the insulator state is the Mott insulator, in which Δ _C is finite and Δ _S vanishes.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. The spin gap Δ S and charge gap Δ C as functions of U and system length N for panels (a)– (d) L0 = 2 and panels (e) and (f) L0 = 3. ε = − U/2.

For superlattices with odd L₀, the MIT is not observed. The charge and spin gaps Δ _C and Δ _S with L₀ = 3 are shown in Figs. 1(e) and 1(f), respectively. It is found that both energy gaps decrease with U increasing for a definite N. In the thermodynamic limit N → ∞ , the gaps vanish and the ground state with L₀ = 3 is always metallic at half filling and the particle– hole symmetric point ε = − U/2. In the previous work for L₀ = 1, the particle– hole symmetrical point is a correlated-metal point at half-filling.^[35] Our calculation shows that for other odd L₀ (e.g., L₀ = 3, 5), this conclusion is kept.

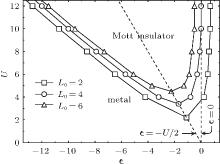
The MIT transition points for superlattices with different even L₀ at half-filling are checked and the result is shown in Fig. 2. It is seen that for larger L₀, Δ _C increases more slowly with U increasing and critical U_c increases. The critical U_c for superlattices with L₀ = 2, 4, and 6 are 2.2, 3.4, and 4.5, respectively. One recalls that this phase transition also happens in the one-dimensional Hubbard model at half-filling where the transition occurs at U = 0. When the superlattice structure is present and there are more free sites in a unit cell, a stronger repulsive interaction is required to give rise to a Mott insulator phase.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Charge gaps for different even L0 in the thermodynamic limit. ε = − U/2.

Next, we turn to the properties of superlattices without particle– hole symmetry. When one observes the effect of orbital energy ε _i, the energy difference between sites is essential. Without loss of generality, ε _i at free sites are regarded as zero and ε _i = ε at repulsive sites. ε is changed to adjust the distribution of electrons. As shown in Fig. 3, we choose superlattices with L₀ = 3 and 4 to demonstrate how ε affects the charge and spin excitations. For odd L₀ (e.g., L₀ = 3), the charge and spin gaps Δ _C and Δ _S always have the same values and are opened beyond the particle– hole symmetric point. This feature indicates that the superlattice with odd L₀ becomes a band insulator at half-filling when the particle– hole symmetry is broken. For even L₀ (e.g., L₀ = 4), the spin excitation is always gapless. For small repulsion U, the system is always metallic while for large U (e.g., U = 8 in Fig. 3(d)), the system persists as a Mott– insulator just around the particle– hole symmetric point ε = − U/2 and the MIT occurs when ε is far away from − U/2. A phase diagram for superlattices with even L₀ is given in Section 4.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Charge gap Δ C (triangles) and spin gap Δ S (squares) as functions of the orbital energy ε for different L0 and U. (a) L0 = 3, U = 1; (b) L0 = 3, U = 8; (c) L0 = 4, U = 1; (d) L0 = 4, U = 8.

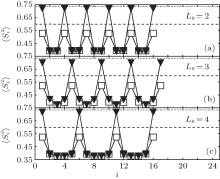
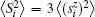
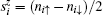
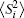
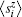
The local moment is usually used to measure the degree of itinerancy in electron lattice systems, where is the net spin or the magnetization. For the Hubbard model at half-filled filling, varies from 3/8 (the limit of complete itinerancy, i.e., U = 0) to 3/4 (the limit of complete localization, i.e., U = ∞ ), and is always 0 because of the lack of spontaneous breaking of symmetry.

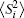
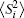
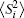
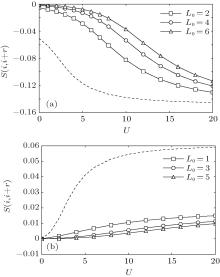
For the superlattice with particle– hole symmetry, figure 4 displays the local moment profile within the range of several periodic cells. Regardless of the superlattice structure and the value of U, always reaches the maximum at repulsive sites and is close to the complete itinerant limit 3/8 at free sites. When U is strong enough, e.g., U = 16, on repulsive sites is comparable with that of the Hubbard model. However, it is not true for weak U. For example, for U = 4 in Fig. 4, is about 0.53, which is smaller than 0.6 of the Hubbard model.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Local moment at site i for L0 = 2 (a), 3 (b) and 4 (c). Squares refer to U = 4 and triangles to U = 16; dashed and dotted lines denote the local moment of the Hubbard model with U = 4 and 16, respectively. ε = − U/2.

Now, we study the static spin structure factor to describe the spin correlation, which is defined as

We consider 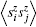instead of ⟨ S_i· S_j⟩ because of the SU(2) symmetry of the Hamiltonian (1). Our numerical results indicate that the finite-size scaling effect of F(q) is insensitive to system size if N is large enough, e.g., N > 100. The following results are for N = 120, 180, 192, 210, 216, and 210 corresponding to L₀ = 1 to 6, respectively. Figure 5 displays F(q) for ε = − U/2 and different L₀ and U. For small repulsive interaction U, F(q) has a peak at q = π for all superlattice structures. As U increases, for odd L₀, there are some slight uplifts in F(q) located at q = k_eπ /(L₀ + L_U), where k_e is an even integer. For example, the uplifts of F(q) occur at q = 2π /6 and 4π /6 for L₀ = 5 in Fig. 5(e); meanwhile, the uplift still holds at q = π for L₀ = 1 and F(q) has a unique peak at q = π in Fig. 5(a). The uplifts of F(q) for a superlattice with odd L₀ only occur at very large U (e.g., U = 18). For even L₀ and large U, e.g., U > 10, multiple peaks appear in F(q), which are located at q = k_oπ /(L₀ + L_U), where k_o is an odd integer. For example, there are 2, 3, and 4 sharp peaks in Figs. 5(b), 5(d), and 5(f) for L₀ = 2, 4, and 6, respectively. Furthermore, the multiple peaks are enhanced with U increasing.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Static spin structure factor F(q) for ε = − U/2 and different L0 and U. (a) L0 = 1; (b) L0 = 2; (c) L0 = 3; (d) L0 = 4; (e) L0 = 5; (f) L0 = 6.

It is worth noting that there is the cusp structure in the Hubbard model for different electron filling density ρ .^[41] For instance, SDW has a cusp at q_max = 2k_F = π ρ for ρ ≤ 1, or q_max = 2k_F = π (2 − ρ ) for ρ ≥ 1. For the superlattice model in Ref. [27], a two-peak structure is observed in a specific electron density region while there is only one peak at q = π at half-filling (see Fig. 6 therein). In our Hubbard superlattices, the multiperiodic SDW is found at half-filling and the particle– hole symmetric point.

In order to understand the above characteristics of static spin structure factors, we consider the local spin correlation . Obviously, the peak of F(q) at q = π results from the antiferromagnetic correlation between the nearest neighboring sites for all superlattices. In Fig. 6, we present the spin correlation S(i_U, i_U + L₀ + 1) between the nearest neighboring repulsive sites, where i_U labels the site with on-site repulsion U. For even L₀, S(i_U, i_U + L₀ + 1) is always antiferromagnetic and enhanced by U. As S(i_U, i_U + L₀ + 1) is strong enough, a new antiferromagnetic period L₀ + 1 emerges. Therefore, the multiple peaks in F(q) appear at q = k_oπ /(L₀ + 1) with k_o being an odd integer. For odd L₀, S(i_U, i_U + L₀ + 1) is ferromagnetic and also increases with U increasing. As S(i_U, i_U + L₀ + 1) is strong enough there appears a local maximum in F(q) at q = k_eπ /(L₀ + 1) with k_e being an even integer.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Spin correlation S(i, i + r) between the nearest neighboring repulsive sites as a function of U for (a) even L0 and (b) odd L0. The dashed lines correspond to the spin correlation between (a) the nearest neighboring sites and (b) the next nearest neighboring sites in the 1D Hubbard model. ε = − U/2.

We have investigated the charge and spin gaps and spin structure in 1D half-filled Hubbard superlattices with one repulsive site and L₀ free sites per unit cell. For odd L₀, the charge and spin gaps always have the same values. There is a correlated-metal phase at the particle– hole symmetric point ε = − U/2. The superlattice is a band insulator beyond ε = − U/2. As U increases, for odd L₀, there are some slight uplifts in the spin structure factor, which results from the ferromagnetic correlation between the repulsive sites. For even L₀, the MIT is observed and the phase diagram is shown in Fig. 7. The system is a Mott insulator around the particle– hole symmetric point ε = − U/2. The spin excitation is always gapless. The charge gap vanishes for small U and opens for U > U_c. In the insulator regime, we observe a multiple-peak structure in the spin structure factor, which results from the antiferromagnetic correlation between the nearest neighboring repulsive sites.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Phase diagram of superlattices with even L0 on the U– ε plane.

Our results show that the electronic and magnetic properties of the Hubbard superlattice model (1) have an interesting odd– even L₀ disparity. Some results can be qualitatively understood by energy band theory. For the superlattice, if L₀ is odd, the length of unit cell is even and the number of bands is also even. At half-filling, half of the bands are filled. The system is metal or insulator depending on the properties of the bands around Fermi level. However, when L₀ is even, half-filling makes the middle band cross the Fermi level and this band splits under the interaction of U, which causes the superlattice to be an insulator. The interaction of U on the band also occurs in the one-band Hubbard model. This kind of odd– even disparity is also found in the linear periodic atomic chains of carbon-transition-metal TM-C_n.^{[42, 43]} The first-principles calculation shows that for linear carbon-transition-metal compounds, the relative position of energy bands depends on the number of carbon atoms. Hence, spin-dependent electronic properties also vary according to odd or even carbon atoms. In conclusion, although the importance of nanoscale spatial inhomogeneity has been widely recognized, ^[32] the effort in experiment and theory should be made to understand properly the consequence of nanoscale inhomogeneity.