The properties of polymers can be affected by spatial, chemical, or interfacial confinement of the polymer. Confinement plays an important role in processes such as lubrication, filtration, colloid stabilization, flow-injection problems, drug delivery applications, etc. Polymers confined in nanopores, nanospheres, or the nanocomposite systems are always considered to be an extension of the thin films on supported substrates.^{[1– 4]} When polymers are confined by restricted volume, there is always a surface/interface that makes the polymers impenetrable. It can greatly affect conformation, ^{[5– 11]} glass transition^{[12– 15]} of polymers, even the self-assembly of block copolymers.^{[16– 21]} The conformational properties of polymer glasses on planar surfaces are widely investigated experimentally and theoretically.^{[10– 12]} Even the curvature of the surface/interface is an important factor to change the phase behavior of polymers.^{[5, 6, 22]} Recently, the glass transition of polymers in rigid cylindrical inorganic (anodic aluminum oxide, AAO) nanopores is studied.^{[7– 9, 23]} Double glass transition temperatures of poly(methyl methacrylate) confined in alumina nanocylinder template were observed.^[7] This shows that the polymers confined in curved surfaces have special properties. We can use these factors to tailor the properties of polymers.

The structural properties of polymer glass near a planar hard wall is well studied.^{[10, 11]} The important factor is the density distribution of polymers in confined states. The effect of density on the polymer glass transition temperature has been investigated by Monte Carlo simulation and mode coupling theory, respectively.^{[10, 11]} Generally, the average density can be obtained in experiments. Confined polymers can show strong local density variations, density oscillations/ fluctuation due to the confinement, which will strongly influence the dynamics as well.^[24] Also the interaction between the surface and the polymer is likely very important.^{[25– 27]} Temperature-dependent density profiles have been observed.^[10] However, the effect of the strength of confinement or the curvature of the hard wall on the structural properties is still unclear. In this work, we consider the polymer glass in a nanocylinder. The radius of the nanocylinder, the length of the polymer, and also the temperature are considered. We also analyze the bond length and the conformation of the polymer under the above conditions.

We consider n polymer chains with length N and segment size a (we set a = 1 here) confined in a nanocylinder with radius R and length L in unit of a. The polymer chains are described by a coarse-grained bead-spring model, where each bead is thought of as representing a few (about 3– 5), successive chemical monomers along the chain. The interactions between the beads are modeled by a Lennard– Jones (LJ) potential U_LJ(r) that is truncated at r_c,

Here r = | r_i − r_j| is the distance between beads at positions r_i and r_j. Constant C is chosen such that U_LJ(r) is continuous at the cutoff distance. We choose the LJ diameter σ = 1 as the length unit, and ε = 1 as the unit of temperature (with Boltzmann’ s constant k_B = 1). The spring connecting two neighboring beads along the chain is described by the so-called “ finitely extensible nonlinear elastic” (FENE) potential

Choosing r₀ = 1.5 and k = 30, the total potential between neighboring beads is U_LJ(r) + U_FENE(r).

The confining cylindrical walls are defined in terms of a wall potential^{[6, 28, 29]}

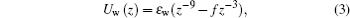
where z is the normal distance from the wall. We assume that the wall atoms can be treated as a continuum of a certain density ρ _w. Note that in order to obtain the equation one has to transform the usual LJ parameters via ε _w = 4π σ ¹²ρ _wε /45 and ε _wf = 2π σ ⁶ρ _wε /3. The value ε _w = 0.1 is used for the polymer beads in this study.

Monte Carlo simulation method is used in the present work. In the Monte Carlo simulations, two types of elementary moves are carried out; local moves that displace a monomer to a nearest neighbor site and pivot moves about the z axis.^{[5, 6]} In all simulations, nN local move attempts were followed by 100n pivot move attempts. We refer to this sequence as one Monte Carlo (MC) step. 10⁶ Monte Carlo steps are performed, and the properties are computed when t > 5 × 10⁵ in order to avoid the effect of the initial configuration.

We systematically analyze the conformational phases of polymers confined in nanocylinders of different radii. The temperature effect is also considered. The polymer density ϕ 0 (= nN/(π R²L)) is set to 0.6, which suffices to make the model exhibit the behavior of dense polymer melts.^{[10, 30]}

3.1. Monomer density profile

The radial density function of polymers in the nanocylinder is represented by ϕ (r). The total number of polymer beads nN in the nanocylinder can be obtained by . Figure 1 presents the radial monomer density profile of polymers in the nanocylinder with N = 8, 16, 32 at R = 6 and T = 4. Here we can see the large oscillations of the density distribution near the hard wall of the nanocylinder. The density oscillation decays near the center of the nanocylinder. The density oscillation for the chain with N = 8 is a little larger near the hard wall, while that for longer chains is smaller. It is easy to understand that the longer chains cannot easily be near the hard wall of the nanocylinder due to the depletion effect.^[31] Compared with long chains, the short polymer chains can have large density oscillations near the inner hard wall of the nanocylinder. This is why two T_g have been observed of polymers with low molecular weight in AAO nanotubes.^[7] In the following part, we present the result based on the polymer glass with N = 8.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Radial density profiles of polymers in the nanocylinder with N = 8, 16, and 32 at R = 6 and T = 4. Note that 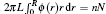, the total number of polymer beads in the nanocylinder is the same below.

Figure 2 gives the radial density profiles of polymers in the nanocylinder with different radii R = 8, 6, 4 at polymer chain length N = 8. When the radius of the nanocylinder is large, the density oscillation near the inner hard wall of the nanocylinder is very large, and the density decays to the average value near the center of the cylinder. When the radius decreases, the density oscillation near the hard surface increases. The oscillation is not only near the hard wall of the cylinder, but diffuses to the center of the cylinder when the radius of the cylinder is small. This result shows that the oscillation is larger in a cylinder with smaller radius. The maximum density oscillation increases as the radius of the nanocylinder decreases. The difference of the density oscillation in nanocylinders with different radii will affect the phase behavior of polymers in the nanocylinder. This different packing density will affect the phase behavior of polymers in nanoscale. For example, the glass transition of polymers poly(methyl methacrylate) in rigid cylindrical inorganic (AAO) nanopores shows double glass transition temperatures.^[7] This shows that the polymers confined in curved surfaces have special properties. Our simulation results confirm the different T_g coming from the different packing density in nanoconfinement.

Fig. 2.

	Figure Option ViewDownloadNew Window
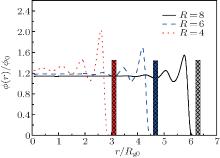	Fig. 2. Radial density profiles ϕ (r) of polymers in the nanocylinder with R = 8, 6, and 4 at N = 8 and T = 4. Rg0 is the radius of gyration of polymers in bulk.

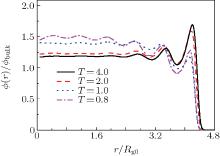
Figure 3 gives the radial density profiles of polymers in the nanocylinder as a function of the radius of the nanocylinder at different temperatures with N = 8 and R = 6. The studied temperatures vary between those of the ordinary liquid and those of the supercooled melt. At higher temperatures, the configurational properties of the polymers close to the walls of the nanocylinder show the following characteristics: the density profiles of the monomers are enhanced at the walls and decay toward the bulk value on the length scale of the bond. This phenomena is also observed for polymers confined in two parallel hard walls.^[10] However, at lower temperatures (such as T = 0.8 and 1.0), the density oscillation is not only near the hard wall of the nanocylinder, but also in the center of the nanocylinder. The strange behavior is that the average density of polymers in the center of the cylinder is higher than those near the inner hard walls at low temperatures.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Radial density profiles ϕ (r) of polymers in the nanocylinder as a function of the radius of the nanocylinder at N = 8 and R = 6.

3.2. Conformational property

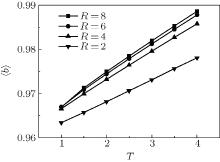
The conformation of polymer chains has great effect on the polymer density in the nanocylinder. Figure 4 shows the radius of gyration of polymers in a nanocylinder as a function of temperature. The overall radius of gyration is shown in Fig. 4(a). The polymer chains in the nanocylinder will contract with decreasing temperature. The contraction is strong when the polymers confined in a nanocylinder with small radius. In order to clearly see how the polymers contract in the smaller nanocylinder at lower temperature, we also give the radius of gyration along the axis and the cross section of the nanocylinder in Fig. 4(b). Note that . From Fig. 4(b), we can see that the almost does not change when decreasing the temperature, while tends to decrease when decreasing the temperature. Hence, the contraction of polymer chains is along the axis when decreasing the temperature. We also note that the radius of gyration of polymers is affected by the radius of the nanocylinder. The is proportional to the radius of the cylinder due to cylindrical confinement, and the of the polymers in smaller nanocylinders shows the larger extension along the axis of the nanocylinder.

Fig. 4.

	Figure Option ViewDownloadNew Window
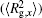
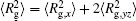
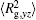
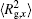
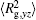
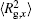
	Fig. 4. Radius of gyration of polymers in the nanocylinder as a function of temperature at N = 8 with R = 8, 6, and 4. (a) 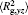, (b) and .

We further consider the bond length of polymers in the nanocylinder. Figure 5 presents the bond length of polymers as a function of temperature with N = 8 at R = 8, 6, 4, and 2. The bond length decreases with lowering temperature. Also, the bond length in the nanocylinder with smaller radius is shorter, which shows that the polymers will contract when they are highly confined in the nanocylinder.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Bond length of polymers as a function of temperature with N = 8 at R = 8, 6, 4, and 2.

From the above conformational properties of polymers in a nanocylinder, we can deduce that both the bonds and the chains tend to align preferentially parallel to the wall (extension along the axis of the nanocylinder) when temperature declines and confinement is high. When the polymers are highly confined and progressively supercooled, all features of the profiles and the tendency of parallel orientation with respect to the walls become more pronounced. Moreover, the oscillation or perturbation introduced by the presence of the walls penetrates deeply into the bulk, decaying on a length scale which is larger than the radius of gyration.

The structural properties of a polymer melt confined in nanocylinders were investigated by Monte Carlo simulation. The polymers show different features close to the inside walls of the nanocylinder. There are several maxima of the density near the wall, which shows that distribution of the polymer in the nanocylinder is not universal. The density profiles of the polymers are enhanced near the wall of the nanocylinder and decay toward the bulk value. That is to say, the nano-confinement causes different packing densities near the wall and far from the wall. Comparing the highest densities near the inside wall of the nanocylinder, we can find that the highest density decreases with increasing radius of the nanocylinder. At lower temperatures, the density excess is not only near the inside wall of the nanocylinder, but also shifts to the center of the nanocylinder when the radius of the nanocylinder is very small.

The radius of gyration along the axis of the nanocylinder tends to contract when the radius of the nanocylinder is small. The bond length of polymers in the nanocylinder decreases a little when confined in a small nanocylinder. When temperature decreases, the polymer chains tend to contract along the axis of the nanocylinder, resulting in a decrease of the bond length. The above results show that the structural properties of polymers in a nanocylinder are not only affected by the curvature of the cylinder, but also by temperature. Our results are very helpful in understanding different packing-induced physical behaviors of polymers in nanocylinders, such as glass transition, crystallization, ^[32] etc.