Spintronics is a possible technology to conquer the bottleneck in electronic industry where the quantum effect becomes remarkable with the size of devices decreasing to nanometers.^{[1– 6]} Besides the half-metal materials, ^{[2, 3, 7]} spin-selective semiconductors^{[8– 10]} are also natural candidates for spintronics. A few kinds of low-dimensional materials are proposed to be spin-selective under applied electric fields, including graphene nanoribbons, ^{[11– 17]} silicene nanoribbons, ^{[18– 20]} germanene nanoribbons, ^{[21, 22]} and so on. The zigzag graphene nanoribbon (ZGNR) is a one-dimensional planar form of carbon, and it is stable with dangling bonds being saturated by hydrogen atoms or other chemical groups like methyl group, fluorine atom, and so on.^{[23– 26]} The spin texture of ZGNR can be tuned by structural modification on the ribbon edges, such as sawtooth zigzag edges, ^{[27– 29]} substitution of carbon atoms, ^{[30, 31]} and Stone– Wales defects.^{[32, 33]} The spin properties of ZGNR wider than four zigzag chains (> 4ZGNR) have been studied a lot. However, the spin texture and electric field effect remain unknown for ultrathin ZGNR with only three or four carbon chains (3ZGNR, 4ZGNR) as shown in Fig.  1. We reveal the coexistence of a normal spin-degenerate conducting mechanism and spin-selective conducting mechanism in such ultrathin ZGNRs by applying an in-plane electric field perpendicular to the direction of the ribbon edge.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Optimized atomic structures of (a) 3ZGNR and (b) 4ZGNR. One unit cell is shown between two parallel slashed lines, and the lattice constant is a. The applied electric field is along the x axis. Black balls are carbon and white ones are hydrogen.

Our first-principles calculations are carried out with the CASTEP package based on the local density approximation (LDA) of CA-PZ^[34] functional using a norm-conserving peseudopotential.^[35] Self-consistent results are obtained with a plane-wave cutoff of 680  eV on a 1× 50× 1 Monkhorst– Pack k-point grid. A supercell with a vacuum layer of 15 Å is used to ensure decoupling between neighboring slabs. For structural relaxation, all atoms are allowed to relax until the atomic forces are smaller than 0.005  eV/Å . The electric field E is applied along the positive direction of the x axis as shown in Fig.  1.

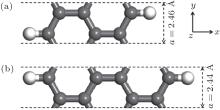
Figure  1 illustrates the atomic structures of 3ZGNR and 4ZGNR. The experimental lattice constant of graphene (2.45  Å ) is used for the initial geometries. Hydrogen atoms are used to saturate the dangling bonds of the carbon atoms on the edges. Both geometries of 3ZGNR and 4ZGNR are fully optimized. After the optimization, the lattice constant increases a little (∼ 0.4%) for 3ZGNR due to the odd number of carbon chains and decreases a little (∼ 0.3%) for 4ZGNR due to the even number of carbon chains. Both structures remain planar.

The critical spin-polarized band structures of 3ZGNR are shown in Fig.  2 with increasing E from 0  V/Å to 0.500  V/Å by a step of 0.005  V/Å . The Fermi level (E_F) is not set to zero. For 0  V/Å , the conduction band minimum (CBM) and the valence band maximum (VBM) are spin-degenerate. Without the applied field, there is only one conduction band minimum, which locates around the X point (CBM_X, K_X = π /a) in the one-dimensional wavevector space. 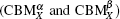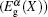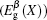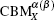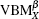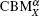As we already know, the CBM_X for wider ZGNRs is split in energy with respect to two spins α and β when field E is applied, and the energy gap of α decreases while that of β increases with increasing field.^[2] For ultrathin ZGNRs, the follows the same rule. Meanwhile, as shown in Fig.  2(b), the second and the higher conduction bands go down in the vicinity of the Γ point with increasing E. For 0.445  V/Å , the CBM at the Γ point (K = 0) overlaps the VBM around the X point (K = π /a) for spin α , and the electrons of spin α can transmit to the spin-degenerate conduction band with a momentum change (Δ P = ħ Δ k, Δ k ≈ 0.43 × 2π /a), i.e., the first conducting channel is open and corresponds to a new CBM around the Γ point (CBM_Γ ) and a new energy gap E_g (Γ ). Moreover, the valence band maximum is spin-splitted when the field E is applied and always changes slightly with increasing E, which is similar for ultrathin and wider ZGNRs. The spin-splitted VBM ( and ) locates around the X point. As a result, the CBM_Γ declines and crosses the and one after the other with increasing E. Increasing E to 0.500  V/Å , the overlaps with the and turns on the second conducting channel.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Band structures of 3ZGNR under increasing applied fields. Bottom panels are enlarged views of the upper panels around EF. For spins, α and β are displayed in red and blue, respectively. Five electric fields of (a) 0  V/Å , (b) 0.200  V/Å , (c) 0.445  V/Å , (d) 0.460  V/Å , and (e) 0.500V/Å are applied to the system respectively.

The spin-polarized band structures of 4ZGNR are shown in Fig.  3 with increasing E from 0  V/Å to 0.500  V/Å by a step of 0.005  V/Å . The E_F is not set to zero either. As shown in Fig.  3(b), when the electric field is applied, the CBM_X and VBM_X of 4ZGNR are spin-splitted, while the conduction bands go down in the vicinity of both Γ and X points, that is, the band structure of 4ZGNR follows the same tendency of 3ZGNR. However, when E is increased to 0.380  V/Å (Fig.  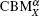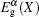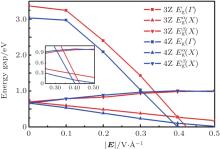3(c)), the normal minimum overlaps with the , i.e., the energy gap closes firstly, and the first conducting channel is open around the X point. It coincides with the wider ZGNRs but not the 3ZGNR. Moreover, with increasing E, 4ZGNR behaves similarly to 3ZGNR: a spin-degenerate CBM around the Γ point emerges and brings a new energy gap E_g (Γ ) correspondingly. If the field E keeps on increasing, the CBM_Γ declines to cross the and at 0.400  V/Å and 0.420  V/Å (Figs.  3(d) and 3(e)), respectively.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Band structures of 4ZGNR under increasing applied fields. Bottom panels are enlarged views of the upper panels around EF. For spins, α and β are displayed in red and blue, respectively. Five electric fields of (a) 0  V/Å , (b) 0.200  V/Å , (c) 0.380  V/Å , (d) 0.400  V/Å , and (e) 0.420  V/Å are applied.

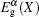
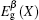
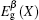
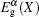
Figure  4 illustrates the relationship between the strength of the electric field E and the spin-splitted energy gap of 3ZGNR and 4ZGNR at different k points, E_g (Γ ), , With increasing E, the energy gap increases while the other spin-splitted energy gap decreases to 0 gradually for both 3ZGNR and 4ZGNR. Then the ribbons become half-metal, which is consistent with the behavior of wider ZGNRs. Meanwhile, the energy gap E_g (Γ ) decreases to 0 when E is increased to 0.445  V/Å and 0.400  V/Å for 3ZGNR and 4ZGNR, respectively, thus the ribbons become metallic. This is a new kind of conducting mechanism for ultrathin ZGNR which does not appear in wider ZGNRs.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Dependence of band gap on the strength of electric field (E) for 3ZGNR (red) and 4ZGNR (blue). The band gap is obtained by LDA calculation.

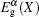
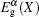
Besides the common X point conduction, both 3ZGNR and 4ZGNR have Γ point conduction. This is a feature of the ultrathin ZGNRs different from wider ZGNRs, and there is a distinction between 3ZGNR and 4ZGNR. In 3ZGNR as shown in Fig.  4, the E for closing E_g (Γ ) (0.445  V/Å ) is lower than that for closing (0.500  V/Å ), and the first conduction channel is around the Γ point along the path of spin-degenerate CBM to VBM. While in 4ZGNR, the E for closing E_g (Γ ) (0.400  V/Å ) is higher than that for closing (0.380  V/Å ), so the first conduction channel is the common one as that in wider ZGNRs along the path of spin-splitted CBM to VBM around the X point. Consequently, increasing the width of the nanoribbon, the conducting mechanism will transition from the Γ point conduction to the common X point conduction in wider ZGNRs.^{[2, 3]} Due to the symmetry of parity, the even– odd effect is obvious in narrow ZGNRs, and it results in the difference of band structure near E_F between 3ZGNR and 4ZGNR, as shown in Figs.  2(b) and 3(b).^{[36, 37]}

The different effects of the electric field between ultrathin and wider ZGNRs originate from the different ribbon widths. It is well known that the localized edge states are ferromagnetic in ZGNRs. The main difference of conducting mechanism between ultrathin ZGNRs and wide ZGNRs is caused by the different distances between the two edges, i.e., the width of the ribbon, and the corresponding interactions between opposite edge states in the narrow ZGNRs.^{[2, 3]} In nanoribbons, E_F locates close to the X point in momentum space under zero bias, and the electrons in the vicinity of E_F locate around the two edges in real space, which contribute to the X point conduction. On the other hand, electrons at the Γ point are distributed across the entire nanoribbon in real space. Thus, the influence of the electric field on the electronic structure depends on the side to surface ratio. For ultrathin nanoribbons, the two edges almost occupy the whole area of the ribbon and the electrons redistribute obviously for both X and Γ points, thus the influence of the electric field is strong for both conducting mechanisms. For wider nanoribbons, only the electrons moving along the edges redistribute obviously, while the electrons at the Γ point are weakly affected because most of them are inside the ribbon. The distributing distance of the localized edge states determines the critical width of ZGNRs. From systematic calculations, we find that 4ZGNR is the critical width. The change of conducting mechanism disappears for ZGNRs wider than 4 carbon chains, and all wide ZGNRs only have one kind of conducting mechanism which is spin-splitted around the X point. In applications, the collaboration and competition between the two conducting mechanisms should be considered, which can be checked and verified by studying the density of states around E_F using spin-polarized scanning tunnelling microscopy (STM) and scanning tunnelling spectroscopy (STS). In addition, only electrons with one kind of spin can be conductive in the X point conduction, while both α and β electrons can be conductive in the Γ point conduction, when the applied electric field increases. This property makes new electronic devices, which are able to work in both conventional (spin-degenerate) or spin-polarized modes, possible.

The conducting mechanism may change due to the underestimation of the band gap in LDA calculations. To check the effect of underestimation, both 3ZGNR and 4ZGNR are also studied with the generalized gradient approximation (GGA) based on PBE functional^[38] under the same precision as the LDA calculations. As we know, the GGA functional always gives a wider band gap than the LDA. The results of GGA are shown in Fig.  5. For 3ZGNR, the results of LDA and GGA are qualitatively the same. For 4ZGNR, the results of LDA and GGA show inverse order of transition between two conducting mechanisms with increasing electric field; it is due to the different deviation in estimation of the band gap in LDA and GGA. The electric fields needed to close the gap between the VBM_X and the spin-degenerate CBM_Γ are analogous for LDA and GGA calculations. Moreover, a much higher electric field is needed to close the gap between the VBM_X and the spin-splitted CBM_X in GGA due to the remarkable band gap around the X point.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. Dependence of band gap on the strength of electric field (E) for 3ZGNR (red) and 4ZGNR (blue). The band gap is obtained by the GGA calculation.

The electric field effect in ultrathin ZGNRs (3ZGNR, 4ZGNR) is studied with density functional theory. New conducting channels are open with increasing applied field. Both Γ point conduction and X point conduction should be considered in applications of ultrathin ZGNRs, which is different from that of the wide ones. The phenomena result from the quantum confinement effect and make new electronic devices working in both conventional or spin-polarized modes possible.