Granular materials are ubiquitous in natural, industrial, mining and geological processes. While they are comprised of many solid particles, their bulk properties exhibit many nonlinear phenomena such as force chains, ^{[1– 3]} surface waves and surface instability, ^{[4, 5]} resistance to penetration, ^[6] segregation, ^{[7, 8]} jamming and clogging, ^{[9– 12]} granular flow, ^{[13– 15]} granular clock, ^{[16, 17]} stress fluctuation, ^[18] etc. Fluidized beds have been widely used in industry for processing granular materials, such as hydrocarbon cracking, coal gasification, drying and mixing, and so on.^{[19, 20]} A plasma fluidized bed (PFB) is a hybrid technology combining the plasma and the gas fluidized bed together.^{[21– 25]} On one hand, plasmas can enhance chemical reaction in the bed without the need of heating the granular bed. Meanwhile, the flowing air in the bed can carry away the heat generated by the plasma, so that the equipment will not be burned. In recent years, some atmospheric pressure discharge sources have been developed, including the atmospheric plasma jet, ^[26] the surface dielectric barrier discharges (DBD)^[27] and the micro-hollow cathode discharge.^{[28, 29]} The technique of the plasma fluidized bed has attracted more and more attention. Mohammedi et al. used a fluidized bed to quench the high-temperature plasma.^[30] Francke et al. used the technique of laser Doppler anemometry to measure the hydrokinetic characteristics of particles in a plasma fluidized bed.^[31]

Previous studies of plasma fluidized beds mainly focused on the chemical reactions in them. It is necessary to comprehensively study the effect of plasma on the fluidization behavior of the granular system. In the environment of plasmas, the granular particles are charged and will behave differently from a normal gas environment. In this paper, we focus on the stabilization effect of plasma on a bubbling fluidized bed. We use corona-induced dielectric barrier discharge (CDBD) to generate plasma at room temperature and air pressure. Our experiments show that the granular bed is strongly affected by the plasma. With the increase in plasma discharge current, the bubbling in the bed is gradually eliminated and the surface fluctuation of the bed is also suppressed. The bubble size decreases monotonically with discharge current. The minimal stabilizing current to eliminate bubbles in the bed is found to increase linearly with flowing air velocity. A simplified model is also proposed to consider the electric Coulomb force. We find that the Coulomb force points inversely to the gradient of particle volume fraction. Therefore, the Coulomb force suppresses the develop of bubbles in the bed.

The experiment is performed in a quasi-two-dimensional fluidized bed, as shown in Fig.  1. The container is made of glass plate 4-mm thick. The inner dimensions of the container are 15-mm wide, 150-mm long, and 500-mm high. Plasma is generated with corona-induced dielectric barrier discharge. This method can generate plasma at room temperature and atmospheric pressure. A bronze plate is fixed at the back of the container as one electrode. The front electrode is an array of 14× 5  pins (diameter 0.4  mm), so as to maintain a uniform discharge of plasma. The horizontal distance between pins is 10  mm, vertical distance is 20  mm. Both electrodes are connected to an AC power supply with a maximum peak voltage of 30  kV and an adjustable frequency ranging from 15  kHz to 30  kHz.

Fig.  1.

	Figure Option ViewDownloadNew Window
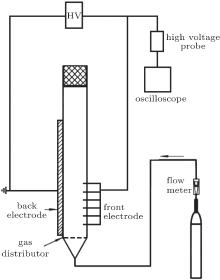	Fig.  1. Side view schematic diagram of the plasma fluidized bed. The fluidized bed is vertical. Gas (air) blows upward to fluidize the granular bed of glass beads.

The granular bed to be fluidized is 400-mm high, and is composed of glass beads of diameter 0.5  mm. The bed is fluidized with air. An air flow meter is adopted to measure the air velocity. The fluidized bed is at air pressure and room temperature T ≈ 25  ° C. Moreover, a digital camera (800× 600 pixels, shutter speed: 60  fps) is adopted to record the fluidization state of the bed. The bubble size in the fluidized bed is measured afterwards by analyzing the captured pictures.

Figure  2(a) shows the voltage and discharge current as a function of time at V_pp = 15  kV. There are many current peaks in the positive cycle of the applied voltage and few current peaks in the negative cycle. It is clear that the discharge events in the two half voltage cycles are different. This asymmetry is distinct from a conventional DBD air reactor between two parallel plate electrodes. The corresponding Lissajous figure is shown in Fig.  2(b). The Lissajous figure is an ellipse, which is different from the typical figure, a parallelogram, in the air reactor. Because of the distortion effect of the field caused by the solid particles, discharge mainly occurs on the surface of the particles. Electrons will be arrested by the particles in the process of plasma discharge. The particles will have negative charges.^[25]

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. (a) Waveforms of the applied voltage and the discharge current at Vpp = 15  kV, and panel (b) is the corresponding Lissajous figure.

According to the Geldart grouping, ^[19] the granular particles used in this fluidized bed belong to the B group, corresponding to a bubbling fluidized bed. In the case, the bed’ s bubbling air velocity v_mb equals its minimum fluidization velocity v_mf. Therefore, when the air speed exceeds the fluidization speed, the excessive air will form bubbles, inducing instability in the bed. Here we show, with plasma, that the fluidization of the granular bed is stabilized. Increasing the plasma discharge current, the bubble size in the system will dramatically decrease and the surface fluctuation is suppressed.

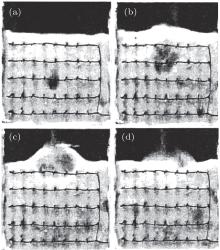
Figure  3 shows a typical evolution of an air bubble in the fluidized bed without plasma at an air velocity of 0.34  m/s. A bubble forms within the granular bed and expands quickly when it moves upward. When the bubble reaches the surface, it creates an obvious apophysis. Finally, the bubble is broken and the apophysis disappears.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Snapshots of the fluidized bed without plasma. (a) A new bubble is forming; (b) the bubble expands; (c) the bubble reaches the granular bed surface; (d) the bubble is broken. Air velocity is 0.34  m/s. In the picture, the black area is air, the white area is solid glass beads.

With the plasma, the fluidized bed becomes much more stable. Figure  4 shows the evolution of the fluidized bed with a plasma discharge current of 1.1  mA. Even with such a small discharge current of plasma, the fluidized bed is obviously stabilized. One can see that bubbles can form in the system, but their expansion is greatly suppressed. At the top surface, the bubble creates a much smaller apophysis.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Snapshots of the plasma fluidized bed with a discharge current 1.1  mA. (a) A new bubble is forming; (b) and (c) bubble expansion is suppressed; (d) the bubble is broken. Air velocity is 0.34  m/s.

Figure  5 shows the fluidized bed with a plasma discharge current of 10.2  mA. The bubble expansion is further suppressed. Meanwhile, air jets appear at the top surface. That is, the air passes the granular bed through the spacings between the particles and creates small air jets.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. Snapshots of the plasma fluidized bed with a discharge current 10.2  mA. (a) A new bubble is forming; (b) and (c) bubble expansion is suppressed, and air jets appear at the surface; (d) the bubble is broken. Air velocity is 0.34  m/s.

Figure  6 shows the fluidized bed with a plasma discharge current of 14.7  mA. Now there is no bubble developing in the system. The air passes through the porous granular bed and creates some air jets at the surface of the bed. We note that the height of the granular bed is slightly expanded by about 5%.

Fig.  6.

	Figure Option ViewDownloadNew Window
	Fig.  6. Snapshot of the plasma fluidized bed with a discharge current 14.7  mA. No visible bubble is detected. Air jets appear at different points on the surface. Air velocity is 0.34  m/s.

Figure  7 shows the surface fluctuation (measured by the height of surface apophysis) with different discharge current. One can see that the fluctuation of the surface monotonically decreases with discharge current. When the discharge current is above 14.7  mA, the surface fluctuation is completely suppressed. With the experiment, we find that the generation speed of new bubbles in the granular bed also decreases monotonically with the discharge current. When the discharge current is above 14.7  mA, there is no visible bubble generated in the granular bed.

Fig.  7.

	Figure Option ViewDownloadNew Window
	Fig.  7. Variation of surface fluctuation (height of apophysis) with plasma discharge current. Air velocity is 0.34  m/s.

Figure  8 shows the variation of mean bubble size with plasma discharge current at air velocities of 0.30  m/s, 0.37  m/s, and 0.44  m/s. One can see that the bubble size decreases with plasma strength. Moreover, the bubble size increases with higher air velocity. With higher air velocity, a higher plasma discharge current is needed to suppress the expansion of air bubbles in the system.

Fig.  8.

	Figure Option ViewDownloadNew Window
	Fig.  8. Variation of average bubble size with plasma discharge current for the cases of different air velocities.

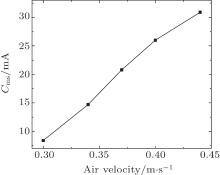
We try to find the minimum stabilizing current C_ms for the system. When the plasma discharge current is above C_ms, the fluidized bed is fully stabilized, so that both the surface fluctuation and bubble size reach zero. Figure  9 shows the variation of minimum stabilizing current C_ms with different injecting air velocities. One can see that C_ms increases linearly with air velocity. A higher air injection needs more plasma to stabilize the system.

Fig.  9.

	Figure Option ViewDownloadNew Window
	Fig.  9. Variation of minimum stabilizing current Cms with air velocity.

In the plasma fluidized bed, the system is in an electric field generated by the charged particles. We need to consider the effect of electric Coulomb force on the motion of particles.

For simplicity, we suppose that the electricity is located at the center of the charged particle. Letting the electric charge of one particle be q_p, the volume of one particle be V_p, the volume of a computation cell be V, and the solid volume fraction in the cell be ϕ _i, we can obtain the electric charge of cell i

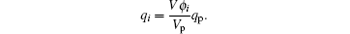
For each cell, we only consider the Coulomb force from neighboring cells. Considering a one-dimensional system of cells i − 2, i − 1, i, i + 1, and i + 2, the Coulomb force on cell i is

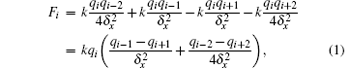
where δ _x is the cell size, k is the Coulomb constant of glass. Inserting the expression of q_i into Eq.  (1), we obtain

In two-dimensional and three-dimensional systems, the Coulomb force is

where δ _x = δ _y = δ _z = h. Therefore, we have F_E ∼ − ∇ ϕ . The Coulomb force F_E is pointing inversely to the gradient of the solid volume fraction, as shown in Fig.  10. The existence of Coulomb force will propel the particles to move to areas with lower solid volume fraction. This effect will make the particles evenly distribute in the system and thus suppress air bubbles. With a high enough electric field strength, the air bubble can not develop in the system.

Fig.  10.

	Figure Option ViewDownloadNew Window
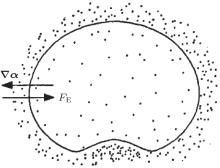	Fig.  10. Illustration of the solid volume fraction gradient ∇ ϕ , and the electric Coulomb force FE. The solid line is a guide to the eye for the border of an air bubble.

In summary, we have studied the stabilization effect of atmospheric pressure plasma on the fluidization behavior of a granular bed. We find that with increase in plasma discharge current, air bubbles are suppressed and the surface fluctuation is mitigated. Our analysis shows that the Coulomb force plays an important role in the stabilization. The electric Coulomb force takes a reversed direction as the gradient of the solid volume fraction. It pushes the particles to move to the void area. By experiment, we find that the minimum stabilization plasma discharge current C_ms increases linearly with air velocity.

Because plasma is composed of very reactive chemical species and can provide energy for the chemical reaction, the plasma fluidized bed is a good candidate for a reactor. The results reported here can benefit the design of plasma fluidized bed reactors. Moreover, the effect of plasma on other granular dynamics could be interesting for the physical society.