The femtosecond laser-based optical frequency comb provides a precise and direct link between optical and microwave frequencies, ^{[1, 2]} its advancements have important impacts on the development of optical atomic clock, ^{[3– 8]} high-precision optical frequency spectroscopy, ^{[9– 16]} and measurement of fundamental constants.^{[17, 18]} In particular, the generation of extreme ultraviolet (XUV) and vacuum ultraviolet (VUV) frequency combs is highly desirable due to the lack of powerful continuous-wave lasers in those spectral regions. In 2005, coherent XUV^[19] and VUV^[20] radiations with a repetition frequency of more than 100  MHz were generated via high-order harmonic generation (HHG) inside femtosecond enhancement cavities (fsECs). Theoretical investigations of the frequency comb structure and coherence of HHG in the VUV– XUV regimes show that the nested comb structure within each of the harmonics ranges from the first harmonic all the way to the cutoff harmonic, ^{[21, 22]} and it has been experimentally demonstrated in the presence of substantial ionization.^{[16, 23– 25]} The combs produced by HHG in an fsEC lack sufficient power for applications owing to the nonlinear response of the HHG medium and the optical damage problems associated with the large average intracavity power.^{[16, 26, 27]} To overcome this drawback, Cingö z et al.^[16] employed powerful high-repetition-rate high-average-power chirped pulse amplified Yb fibre lasers to excite the enhancement cavity to keep the intracavity pulse energy high, and a robust fsEC to mitigate the nonlinear response of the HHG medium. They realized the generation of XUV frequency combs up to the 27th harmonic order (wavelength of 40  nm).

On the other hand, Son and Chu^[28] recently presented a theoretical nonperturbative investigation for the coherent control of multiphoton resonance dynamics and the enhancement of HHG driven by intense frequency-comb laser fields by employing an extension version of the many-mode Floquet theory (MMFT).^{[29– 33]} For a two-level system, it is shown that HHG spectra driven by intense frequency-comb lasers can be dramatically enhanced by tuning the carrier-envelope phase (CEP) shift due to the simultaneous multiphoton resonance among all the comb frequencies. This multiphoton-resonant enhancement (MRE) promises an alternative method to achieve a powerful frequency comb structure in the VUV and/or XUV region, without increasing the intensity of the driving frequency-comb laser fields.

However, the recent theoretical investigation of atomic hydrogen driven by intense frequency-comb laser fields shows that the MRE factor of HHG spectra in the realistic atomic system is much smaller than that in the two-level system, ^{[28, 34]} and the multi-level structure of the realistic atomic system is proposed to be the major cause. It has not been clarified which levels, s, d, or p levels, in the realistic atomic hydrogen system are dominant for the decrease of the MRE factor. To answer this question, we theoretically investigate the multiphoton resonance dynamics and the HHG spectra of three-level systems, the simplest multi-level systems, driven by frequency-comb laser fields. The third level is coupled to either the ground or the excited level of a two-level system, to simulate the role of s, d, or p levels in the MRE dynamics. The investigations about different coupling conditions show that the dipole interaction between the excited level of the two-level system and other levels, i.e., s and d levels in the hydrogen atom, plays a prominent role in the multiphoton dynamics, and it is responsible for the decrease of the MRE factor.

The paper is organized as follows. In Section 2, we briefly present the MMFT for the treatment of the interaction between a quantum system and an intense frequency-comb laser field. In Section 3, we apply the MMFT to study the multiphoton resonance dynamics and the HHG spectra of three (two)-level systems driven by frequency-comb laser fields. The conclusion is given in Section 4.

The frequency-comb laser consists of spectral comb lines in the frequency domain^[2]

where ω _r is the repetition angular frequency, m is an integer index, and ω _δ is the offset angular frequency (0 ≤ ω _δ ≤ ω _r). Without loss of generality, these comb frequencies can be written as

where k is an integer index, and ω ₀ is the main angular frequency defined by

where [ ] is the round function, and ω _c is the carrier frequency.

A frequency-comb laser field is a train of pulses with a CEP shift from pulse to pulse Δ ϕ in the time domain, and can be expressed as

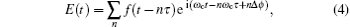
where τ = 2π /ω _r is the time interval between pulses, f(t) = f₀e^{− t2/2σ 2} is the envelope function for each pulse, f₀ is the peak amplitude, and σ is the standard deviation of a Gaussian function. The Δ ϕ determines all absolute positions of frequencies in the comb structure by setting an offset frequency ω _δ = Δ ϕ /τ . Equation  (4) can also be expressed as the summation of components of discrete comb frequencies^[28]

where E_k is the field amplitude of comb frequency ω _k. The infinite summation over k in Eq.  (5) is done with the truncation approximation and a finite integer number N is chosen to approximately reproduce the frequency-comb field and make sure the calculation is accessible and convergent. In our calculation, N is chosen such that E_k < 1 × 10^{− 15}  a.u. (corresponding to intensity 3.51 × 10^{− 14}  W/cm²) when | k| > N.

Considering the interaction of an atomic or molecular system with a linearly polarized frequency-comb laser field in the z direction, including (2N + 1) comb frequencies, we have the total Hamiltonian

where Ĥ ₀(r) is the unperturbed Hamiltonian of the atomic or molecular system and μ (r) is the electric dipole moment operator. Note that the time-depedent Hamiltonian in Eq.  (6) is bichromatic, containing two independent frequencies ω ₀ and ω _r.

By employing the MMFT, ^{[30, 31]} the time-dependent Schrö dinger equation with the Hamiltonian  (6) can be converted into an equivalent time-independent generalized Floquet matrix eigenvalue problem. We employ the basis vectors in the two-mode Floquet formalism

where α is the system index, and n and m are Fourier components of ω ₀ and ω _r, respectively. In the representation spanned by the basis vectors {| α nm〉 }, the time-independent generalized Floquet matrix eigenvalue equation can be written as

where λ and | λ 〉 are the quasienergy eigenvalues and eigenvectors, respectively. Details of the Floquet matrix are found in Ref.  [34]. Solving the eigenvalue problem, we can obtain a set of quasienergies λ _{γ nm} and the corresponding eigenvectors | λ _{γ nm}〉 which satisfy the orthonormality condition.^[29]

The time-averaged transition probability can be computed from the quasienergy eigenvectors^{[30, 31]}

and the induced dipole moment can be expanded in double Fourier series^[28]

Then the harmonic generation spectra in length form can be expressed as

where ω = nω ₀ + mω _r if n and m are given. The harmonic order is defined by ω /ω _c and can be a fractional number because of the comb structure of frequencies.

In this section, we first investigate the multiphoton dynamics and HHG spectra of three-level systems driven by frequency-comb laser fields to study their dependence on the level structure. The laser parameters are carrier frequency 563.5  THz (corresponding to ω _c = 0.0856454  a.u. and wavelength 532  nm) and repetition frequency 10  THz (corresponding to ω _r = 1.51983 × 10^{− 3}  a.u. and pulse separation τ = 0.1  ps), which are generated from a train of Gaussian pulses with 20  fs full width at half maximum (FWHM). The three-level systems can be classified into two types: the gc-type three-level system in which the third level | c〉 is dipole-allowed with the ground level | g〉 ; and the ec-type three-level system in which the third level | c〉 is dipole-allowed with the ground level | e〉 , as shown in Figs.  1(b) and 1(c), respectively. The energy separation between | e〉 and | g〉 is ħ ω _ge = ε _e – ε _g = 0.25  a.u. which corresponds to the three-photon dominant resonance regime (ω _ge ≈ 3ω _c), and the transition dipole moment 〈 g| | e〉 = 0.1  a.u. is used. The dipole moment 〈 g| | c〉 in the gc-type three-level system is set to be 0.1  a.u., while 〈 e| | c〉 in the ec-type is set to be 0.2  a.u. For the gc (ec)-type three-level system, various values of energy separation ħ ω _gc = ε _c – ε _g are used in the calculations, and the case of ħ ω _gc = 0.23  a.u. is taken as a general example, in which the third level | c〉 is far off single/multi-photon resonance with either the ground or excited level.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. (a) The two-level system. The energy separation between ground and excited levels is ħ ω ge = ε e – ε g = 0.25  a.u. (b) The gc-type three-level system in which the third level | c〉 is dipole-allowed with the ground level | g〉 . (c) The ec-type three-level system in which the third level | c〉 is dipole-allowed with the excited level | e〉 .

Figures  2(a) and 2(b) show the HHG spectra of gc- and ec-type three-level systems, respectively, driven by a frequency-comb laser field with the peak intensity 1 × 10¹⁴  W/cm². For the gc-type three-level systems, spectra with CEP shift Δ ϕ /2π = 0.1 (off-resonance) and 0.170667 (near-resonance) are shown, and for the ec-type three-level systems, spectra with CEP shift Δ ϕ /2π = 0.1 (off-resonance) and 0.162748 (near-resonance) are displayed. The HHG spectra of the two-level system with Δ ϕ /2π = 0.1 (off-resonance) and 0.168295 (near-resonance) are also plotted for comparison. It shows that the dipole interaction with the third level leads to the enhancement of the HHG spectra. In particular, the enhancement effect in the ec-type systems is larger than that in the gc-type systems. Figures  2(c) and 2(d) show the time-averaged transition probabilities from | g〉 to | e〉 , P_{g→ e}, as a function of Δ ϕ in gc- and ec-type three-level systems, respectively. The width of peak Δ ν is broadened from Δ ν /ω _r = 3.3 × 10^{− 5} in the two-level system to Δ ν /ω _r = 7.1 × 10^{− 5} in the gc-type three-level system, and to Δ ν /ω _r = 1.62 × 10^{− 4} in the ec-type three-level system. The calculations with various values of ħ ω _gc in gc- and ec-type three-level systems also demonstrate that the effect of the ec-type interaction is much more remarkable than that of the gc-type interaction. In the ec-type three-level system, the electron can be excited from | g〉 to | e〉 , oscillates between | e〉 and | c〉 , and finally falls back to | g〉 . During this round trip, dipole radiations may occur multiple times. While in the gc-type three-level system, only once dipole radiation occurs during the ground– excited– ground round trip, making the enhancement less effective than that in the ec-type three-level system.

Fig.  2.

Figure Option ViewDownloadNew Window

Fig.  2. (a) and (b) Enhancement of HHG spectra by varying CEP shift in gc- and ec-type three-level systems, respectively. For comparison, HHG spectra of the two-level system with Δ ϕ /2π = 0.1 (off-resonance) and 0.168295 (near-resonance) are plotted with thin red dashed and solid lines, respectively. All comb peaks are connected by a line for clarity. (c) and (d) Pg→ e as a function of Δ ϕ in gc- and ec-type three-level systems, respectively. For comparison, Pg→ e in the two-level system is plotted with a red dashed line. The energy separation ħ ω gc = 0.23  a.u. The parameters used are peak intensity 1 × 1014  W/cm2, carrier frequency 563.5  THz, and repetition frequency 10  THz of 20  fs FWHM Gaussian pulses.

In the following, we focus on the multiphoton dynamics and HHG spectra of the ec-type three-level system driven by frequency-comb laser fields. First of all, we study their dependence on the level position of | c〉 by assuming the same dipole moment 〈 e| | c〉 = 0.2  a.u. In Fig.  3 we plot P_{g→ e} as a function of Δ ϕ for the ec-type three-level systems with energy separations ħ ω _gc = 0.23  a.u. and 0.27  a.u. with different peak intensities. It shows that the resonance peak positions are shifted when the level position of | c〉 is changed. The widths of the resonance peaks with ħ ω _gc = 0.23  a.u. and 0.27  a.u. are almost the same. For instance, Δ ν /ω _r = 8.7 × 10^{− 3} for ħ ω _gc = 0.23  a.u. and Δ ν /ω _r = 8.6 × 10^{− 3} for ħ ω _gc = 0.27  a.u. with the peak intensity 1 × 10¹⁵  W/cm². At the same time, the HHG spectra of the ec-type three-level system with energy separations ħ ω _gc = 0.23  a.u. are almost the same as those with ħ ω _gc = 0.27  a.u., as displayed in Table  1. The level position of | c〉 determines the energy shift of the | e〉 level in external fields due to the dipole interaction, while its effect on the HHG spectra is little. The calculations with various values of ħ ω _gc, such as 0.205  a.u., 0.255  a.u., and 0.295  a.u., reveal the same result.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. The Pg→ e as a function of Δ ϕ in ec-type three-level systems with ħ ω gc = 0.23 (solid line) and 0.27  a.u. (dashed line). The peak intensity of the frequency-comb laser field is (a) 1 × 1014  W/cm2 and (b) 1 × 1015  W/cm2. Other parameters used are the same as those in Fig.  2.

Table 1.

Table 1.

Table 1. The HHG spectra of ec-type three-level systems with different energy separations ħ ω gc and different laser peak intensities by tuning CEP shift Δ ϕ . n is the harmonic order of the maximum peak for each harmonic and P(nω c) is the corresponding HHG power spectral value at ω = nω c. The label A indicates the near-resonance cases: Δ ϕ /2π = 0.162748 and 0.173653 for ħ ω gc = 0.23  a.u. and 0.27  a.u., respectively, at 1 × 1014  W/cm2; Δ ϕ /2π = 0.152426 and 0.258111 for ħ ω gc = 0.23  a.u. and 0.27  a.u., respectively, at 1 × 1015  W/cm2. While B indicates the off-resonance cases with Δ ϕ /2π = 0.1. The numbers in brackets indicate the power of 10. The other laser parameters used are the same at those in Fig.  3. 1 × 1014  W/cm2 1 × 1015  W/cm2 ε gc = 0.23  a.u. ε gc = 0.27  a.u. ε gc = 0.23  a.u. ε gc = 0.27  a.u. A B A B A B A B n P(nω c) n P(nω c) n P(nω c) n P(nω c) n P(nω c) n P(nω c) n P(nω c) n P(nω c) 2.92 2.50[− 3] 2.93 3.48[− 9] 2.92 2.49[− 3] 2.93 1.41[− 9] 2.92 2.07[− 3] 2.92 3.14[− 6] 2.92 2.46[− 3] 2.93 2.69[− 6] 4.91 7.75[− 11] 4.96 3.00[− 16] 4.91 1.49[− 10] 4.96 2.06[− 16] 4.94 1.35[− 8] 4.98 1.33[− 11] 4.92 7.52[− 9] 4.96 2.45[− 11] 6.89 4.88[− 18] 6.96 2.14[− 23] 6.91 9.52[− 18] 6.96 1.47[− 23] 6.94 8.58[− 14] 6.99 7.69[− 17] 6.93 4.75[− 14] 6.96 1.78[− 16] 8.88 1.33[− 25] 8.96 6.45[− 31] 8.88 2.28[− 25] 8.94 3.60[− 31] 8.93 1.97[− 19] 8.96 1.69[− 22] 8.93 1.25[− 19] 8.96 4.94[− 22] 10.91 2.40[− 25] 10.95 2.09[− 28] 10.94 1.77[− 25] 10.95 7.17[− 28]

Table 1. The HHG spectra of ec-type three-level systems with different energy separations ħ ω gc and different laser peak intensities by tuning CEP shift Δ ϕ . n is the harmonic order of the maximum peak for each harmonic and P(nω c) is the corresponding HHG power spectral value at ω = nω c. The label A indicates the near-resonance cases: Δ ϕ /2π = 0.162748 and 0.173653 for ħ ω gc = 0.23  a.u. and 0.27  a.u., respectively, at 1 × 1014  W/cm2; Δ ϕ /2π = 0.152426 and 0.258111 for ħ ω gc = 0.23  a.u. and 0.27  a.u., respectively, at 1 × 1015  W/cm2. While B indicates the off-resonance cases with Δ ϕ /2π = 0.1. The numbers in brackets indicate the power of 10. The other laser parameters used are the same at those in Fig.  3.

Then we investigate the multiphoton dynamics and HHG spectra of the ec-type three-level system driven by frequency-comb laser fields with different laser peak intensities. Figure  4 shows P_{g→ e} as a function of Δ ϕ in the ec-type three-level system with energy separation ħ ω _gc = 0.23  a.u., dipole moment 〈 e| | c〉 = 0.2  a.u., and peak intensities 1 × 10¹⁵  W/cm² and 2.5 × 10¹⁵  W/cm². The widths of the resonance peaks are Δ ν /ω _r = 8.7 × 10^{− 3} at 1 × 10¹⁵  W/cm², and Δ ν /ω _r = 2.3 × 10^{− 2} at 2.5 × 10¹⁵  W/cm², while the minimum values of P_{g→ e} are about 10^{− 3} and 10^{− 2}, respectively. The comparison with the two-level system driven by the same frequency-laser fields suggests that the multiphoton dynamics are modified by the dipole interction between | e〉 and | c〉 , and the modification becomes larger as the laser peak intensity increases.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. The Pg→ e as a function of Δ ϕ in ec-type three-level systems with dipole moment 〈 e| | c〉 = 0.2  a.u., energy separation ħ ω gc = 0.23  a.u., and peak intensities (a) 1 × 1015  W/cm2 and (b) 2.5 × 1015  W/cm2. For comparison, Pg→ e in the two-level system is plotted with a red dashed line. Other parameters used are the same as those in Fig.  2.

In Table  2, we list the spectral values of the HHG maximum peaks for the near- and off-resonance cases with several peak intensities. The HHG peaks can be dramatically enhanced by varying the CEP shift due to the simultaneous multiphoton resonances. With the laser peak intensities 1 × 10¹⁴  W/cm², 1 × 10¹⁵  W/cm², and 2.5 × 10¹⁵  W/cm², the MRE factors are about 10⁵, 10³, and 10², respectively. These values are smaller than those in the two-level system driven by the same laser fields as presented in Ref.  [28]. The dipole interaction of the excited level | e〉 with | c〉 may lead to the smaller MRE factor. It is easy to generalize that the MRE factors of the HHG spectra in realistic atomic/molecular systems would be much smaller than those in the two-level system, since there are multiple levels dipole-allowed with the excited level. This generalization is consistent with the calculation results presented in Ref.  [34].

Table 2.

Table 2.

Table 2. The HHG spectra of ec-type three-level systems with different peak intensities by tuning CEP shift Δ ϕ . n is the harmonic order of the maximum peak for each harmonic and P(nω c) is the corresponding HHG spectral value at ω = nω c. The label A indicates the near-resonance cases: Δ ϕ /2π = 0.162748, 0.487884, and 0.476286 for peak intensities 1 × 1014  W/cm2, 1 × 1015  W/cm2, and 2.5 × 1015  W/cm2, respectively. While B indicates the off-resonance cases with Δ ϕ /2π = 0.3. The numbers in brackets indicate the power of 10. The energy separation ħ ω gc = 0.23  a.u. and the dipole moment 〈 e| | c〉 = 0.2  a.u. The other laser parameters used are the same at those in Fig.  4. 1 × 1014  W/cm2 1 × 1015  W/cm2 2.5 × 1015  W/cm2 A B A B A B n P(nω c) n P(nω c) n P(nω c) n P(nω c) n P(nω c) n P(nω c) 2.92 2.50[− 3] 2.93 3.48[− 9] 2.92 2.46[− 3] 2.92 2.68[− 6] 2.92 2.40[− 3] 2.93 2.94[− 5] 4.91 7.75[− 11] 4.96 3.00[− 16] 4.92 7.52[− 9] 4.96 2.45[− 11] 4.92 4.51[− 8] 4.96 1.80[− 9] 6.89 4.88[− 18] 6.96 2.14[− 23] 6.93 4.75[− 14] 6.96 1.78[− 16] 6.93 1.82[− 12] 6.96 8.43[− 14] 8.88 1.33[− 25] 8.96 6.45[− 31] 8.93 1.25[− 19] 8.96 4.94[− 22] 8.94 3.07[− 17] 8.96 1.49[− 18] 10.94 1.77[− 25] 10.95 7.17[− 28] 10.94 2.73[− 22] 10.95 1.37[− 23] 12.94 1.43[− 27] 12.95 7.46[− 29]

Table 2. The HHG spectra of ec-type three-level systems with different peak intensities by tuning CEP shift Δ ϕ . n is the harmonic order of the maximum peak for each harmonic and P(nω c) is the corresponding HHG spectral value at ω = nω c. The label A indicates the near-resonance cases: Δ ϕ /2π = 0.162748, 0.487884, and 0.476286 for peak intensities 1 × 1014  W/cm2, 1 × 1015  W/cm2, and 2.5 × 1015  W/cm2, respectively. While B indicates the off-resonance cases with Δ ϕ /2π = 0.3. The numbers in brackets indicate the power of 10. The energy separation ħ ω gc = 0.23  a.u. and the dipole moment 〈 e| | c〉 = 0.2  a.u. The other laser parameters used are the same at those in Fig.  4.

Since dipole moments between levels in realistic atomic/molecular systems are quite different from each other, we study the dependence of the HHG spectra in the ec-type three-level systems on the dipole moment 〈 e| | c〉 . Table  3 lists the spectral values of the HHG maximum peaks for the near- and off-resonance cases with different dipole moments 〈 e| | c〉 , the same energy separation ħ ω _gc = 0.27  a.u., and the peak intensity 2.5 × 10¹⁵  W/cm². The dipole interaction with a larger dipole moment makes the MRE factor smaller, although the dipole transition between | e〉 and | c〉 is far off-resonance with the carrier frequency. Now we can give an interpretation about the dependence of multiphoton dynamics and HHG spectra on the multi-level structure. Taking the atomic hydrogen as an example, when the carrier frequency is chosen for the multiphoton dominant resonance between 1s and 3p states, the dipole interaction of 1s and/or 3p with other states enhances the HHG spectra. Particularly, the dipole interactions of 3p with other states, such as 3p– 2s and 3p– 4d transition, whose dipole moments are much larger than others, make the MRE factor of the HHG spectra smaller than that in the two-level system, even though these dipole interactions are far off single/multi-photon resonance with the comb frequencies of the driving laser field.

Table 3.

Table 3.

Table 3. The HHG spectra of ec-type three-level systems with different dipole moments 〈 e| | c〉 by tuning CEP shift Δ ϕ . n is the harmonic order of the maximum peak for each harmonic and P(nω c) is the corresponding HHG spectral value at ω = nω c. The label A indicates the near-resonance cases: Δ ϕ /2π = 0.3020, 0.3910, and 0.5251 for 〈 e| | c〉 = 0.1  a.u., 0.2  a.u., and 0.3  a.u., respectively. While B indicates the off-resonance cases with Δ ϕ /2π = 0.5, 0.6, and 0.7 for 〈 e| | c〉 = 0.1  a.u., 0.2  a.u., and 0.3  a.u., respectively. The numbers in brackets indicate the power of 10. The energy separation ħ ω gc = 0.27  a.u. The laser peak intensity is 2.5 × 1015  W/cm2. The other laser parameters used are the same at those in Fig.  2. 〈 e| | c〉 = 0.1 a.u. 〈 e| | c〉 = 0.2 a.u. 〈 e| | c〉 = 0.3 a.u. A B A B A B n P(nω c) n P(nω c) n P(nω c) n P(nω c) n P(nω c) n P(nω c) 2.93 1.70[− 3] 2.92 7.98[− 7] 2.91 1.11[− 3] 2.92 8.04[− 5] 2.92 1.71[− 3] 2.93 2.86[− 4] 4.94 9.19[− 9] 5.01 1.45[− 12] 4.96 6.91[− 8] 5.04 6.93[− 10] 5.02 2.38[− 7] 4.96 2.69[− 8] 6.96 8.92[− 14] 7.04 1.25[− 17] 6.99 2.78[− 12] 6.96 8.43[− 14] 7.04 3.02[− 11] 6.99 2.33[− 12] 8.96 3.48[− 19] 9.06 4.15[− 23] 8.99 3.96[− 17] 9.11 2.60[− 19] 9.06 1.16[− 15] 9.02 9.91[− 17] 10.99 2.92[− 22] 11.13 1.74[− 24] 11.09 2.39[− 20] 11.05 3.26[− 21] 13.13 3.71[− 25] 13.08 7.21[− 26]

Table 3. The HHG spectra of ec-type three-level systems with different dipole moments 〈 e| | c〉 by tuning CEP shift Δ ϕ . n is the harmonic order of the maximum peak for each harmonic and P(nω c) is the corresponding HHG spectral value at ω = nω c. The label A indicates the near-resonance cases: Δ ϕ /2π = 0.3020, 0.3910, and 0.5251 for 〈 e| | c〉 = 0.1  a.u., 0.2  a.u., and 0.3  a.u., respectively. While B indicates the off-resonance cases with Δ ϕ /2π = 0.5, 0.6, and 0.7 for 〈 e| | c〉 = 0.1  a.u., 0.2  a.u., and 0.3  a.u., respectively. The numbers in brackets indicate the power of 10. The energy separation ħ ω gc = 0.27  a.u. The laser peak intensity is 2.5 × 1015  W/cm2. The other laser parameters used are the same at those in Fig.  2.

We have investigated the multiphoton dynamics and HHG spectra of three-level systems driven by intense frequency-comb laser fields. The many-mode Floquet theory is employed to treat the interaction between the three-level systems and the frequency-comb laser fields. We find that the effect of the ec-type dipole interaction is much more prominent than that of the gc-type one. The dipole interaction of the excited level of the two-level system with the third level reduces the MRE factor of the HHG spectra. And the dipole interaction with a larger dipole moment makes the MRE factor of the HHG spectra smaller. The results well explain the great difference of the MRE factors between the two-level system and the realistic atomic hydrogen.