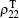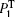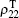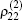Cite this Article
Pei Li-Ya†, Niu Jin-Yan, Wang Ru-Quan, Qu Yi-Zhi, Zuo Zhan-Chun, Wu Ling-An, Fu Pan-Ming‡. Relationship between electromagnetically-induced transparency and Autler–Townes splitting in a Doppler-broadened system . Chinese Physics B, 24(7): 074203  
Permissions
Relationship between electromagnetically-induced transparency and Autler–Townes splitting in a Doppler-broadened system
Pei Li-Ya†a), Niu Jin-Yanb), Wang Ru-Quanc), Qu Yi-Zhia), Zuo Zhan-Chunc), Wu Ling-Anc), Fu Pan-Ming‡c)
College of Material Sciences and Optoelectronic Technology, University of the Chinese Academy of Sciences, Beijing 100049, China
School of Mathematics, Physics and Biological Engineering, Inner Mongolia University of Science and Technology, Baotou 014010, China
Laboratory of Optical Physics, Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China

†Corresponding author. E-mail: peiliya@ucas.ac.cn

‡Corresponding author. E-mail: pmfu@aphy.iphy.ac.cn

*Project supported by the National Natural Science Foundation of China (Grant Nos. 11404330, 11274376, 61308011, and 11474347), the NSAF, China (Grant No. U1330117), the National Basic Research Program of China (Grant Nos. 2013CB922002 and 2010CB922904), and the China Postdoctoral Science Foundation (Grant No. 119103S239).

Abstract

We study the relationship between electromagnetically-induced transparency (EIT) and Autler–Townes (AT) splitting in a cascade three-level Doppler-broadened system. By comparing the absorption spectrum with the fluorescence excitation spectrum, it is found that for a Doppler-broadened system, EIT resonance cannot be explained as the result of quantum interference, unlike the case of a homogeneously broadened system. Instead, the macroscopic polarization interference plays an important role in determining the spectra of EIT and AT splitting, which can be explained within the same framework when being detected by the absorption spectra.

PACS: 42.50.Gy; 42.50.Hz
Keyword: electromagnetically-induced transparency; polarisation interference; Autler–Townes splitting
1. Introduction

To study the important phenomenon of electromagnetically-induced transparency (EIT), [1– 11 people usually use the theoretical model of a three-level system, which is also employed in analysis of Autler– Townes (AT) splitting.[12] Physically, the two effects of EIT and AT splitting are very similar that, dressed states are induced by the so-called coupling or pump field, and then probed through a transition to or from a third level. Furthermore, when a probe field is tuned to the zero-field resonance frequency, both phenomena of EIT and AT splitting can give rise to transparency in an absorption profile.

Recently, the relationship between EIT and AT splitting has been reconsidered by many authors. It is found that depending on the strength of the coupling field, the linear absorption can be expressed either as the difference between two Lorentzian profiles centered at zero frequency with one broad and the other narrow or as the sum of two well-separated Lorentzian profiles with similar widths.[13, 14] Using this theory, Anisimov et al.[15] introduced a method based on Akaikes information criterion to describe the transition from AT splitting to EIT as the pump power decreases. Relevant experimental tests were performed by Giner et al.[16] In this paper we shall study the relationship between EIT and AT splitting in a Doppler-broadened system by comparing the absorption spectrum with the fluorescence excitation spectrum. The motivation for this study is that the absorption spectrum shows a transition from AT splitting to EIT, while the fluorescence excitation spectrum exhibits simply the AT effect. As is well known, quantum interference is a characteristic of a single atom. However, in a Doppler-broadened system there are thousands of atoms with different velocities, so the role of quantum interference in EIT is not clear in this system. It is found that for the Doppler-broadened system the macroscopic effect is more crucial in comparison with the quantum interference. Moreover, it requires to consider the destructive polarization interference between atoms of different velocities.

It is worth mentioning that the problem of EIT in Doppler-broadened systems is not new and has been studied extensively both theoretically and experimentally. For example, Gea-Banacloche et al.[17] discussed the conditions for obtaining EIT with a weak coupling field in a Doppler-broadened cascaded system. Shepherd et al.[18] studied the wave-number-ratio dependence of the EIT resonance. The narrowing of this resonance in a Doppler-broadened medium has been studied by Javan and co-workers.[19, 20] On the experimental side, the subnatural linewidth for probe absorption in an EIT medium has been observed by Iftiquar.[21] On the other hand, fluorescence excitation spectroscopy has been employed widely to study the AT effect. For example, Ahmed and Lyyra[22] analyzed theoretically the AT splitting in a Doppler-broadened three-level cascade system. Relevant experiments have been performed in a three-level Na2 open molecular cascade system, where, for moderate Rabi frequencies, the fluorescence line shape from the uppermost level in the system depends strongly on the wave-number ratio of the two laser fields.[23]

2. Model and method
2.1. Basic equations

Let us consider a closed cascade three-level system (Fig.  1), where the states between | 0〉 and | 1〉 and between | 1〉 and | 2〉 are coupled by dipolar transitions with resonant frequencies and and dipole moment matrix elements μ 1 and μ 2, respectively. A strong coupling field (beam 2) of frequency ω 2 resonantly couples the transition from | 1〉 to | 2〉 , while a weak probe field (beam 1) of frequency ω 1 is applied on the transition | 0〉 − | 1〉 . The effective Hamiltonian is

where is the detuning, and E1 and E2 are the complex incident laser fields of the probe and coupling fields, respectively. The density matrix equations with relaxation terms included are given by

from which we obtain the following equations:

Here Ω i = μ iEi/ħ are the coupling coefficients, Γ ij is the transverse relaxation rate between states | i〉 and | j〉 , and γ 1 (γ 2) is the relaxation rate from | 1〉 to | 0〉 (| 2〉 to | 1〉 ). Here, we have the relation Γ ij = (γ i+ γ j)/2.

Fig.  1. Energy-level diagram for EIT resonance and fluorescence excitation spectroscopy in a cascade three-level system.

In the EIT resonance experiment, the absorption of the probe beam is related to the off-diagonal matrix element ρ 10. On the other hand, in the fluorescence excitation spectroscopy, the intensity of the fluorescence is proportional to the population ρ 22. We first calculate ρ 10 and ρ 20 to the first order in Ω 1 but to all orders in Ω 2. By setting dρ 10/dt = dρ 20/dt = 0 and using the conditions: and , we obtain

We then calculate ρ 22 to the second order in Ω 1. By setting dρ 21/dt = dρ 12/dt = dρ 11/dt = dρ 22/dt = 0, we obtain

As mentioned in Ref.  [22], the polarization P1 = Nμ 1ρ 10 which is responsible for the EIT resonance can be decomposed into linear and nonlinear parts, i.e.,

Here,

The EIT resonance reflects mainly the characteristic of the nonlinear polarization . Specifically, there are three poles for . Let us consider the case of Δ 2 = 0. In the limit of Γ 10 ≫ Γ 20 and | Ω 2 | 2 ≫ Γ 10Γ 20, we have Imwhen Δ 1 is at the resonance of the dressed state, which occur at Δ 1 = ± | Ω 2 | . As a result, the probe beam undergoes absorption. By contrast, for the resonance at Δ 1 = 0, we have Im, therefore the probe beam exhibits amplification. Physically, ρ 20 is established through a two-photon transition from | 0〉 to | 2〉 , so it requires absorption of a photon from the probe beam at a frequency Δ 1 = ± | Ω 2 | detuned from the one-photon resonance. On the other hand, after the two-photon coherence ρ 20 is induced, scattering of the coupling beam leads to the stimulated emission of a photon at the frequency of the probe beam. This stimulated emission will suppress the linear absorption of the probe field, and thus induce transparency.

2.2. Population and polarization in Doppler-broadened systems

Considering a Doppler-broadened system, the total population and polarization are given by

respectively. Here, υ is the atomic velocity, with , m is the mass of an atom, K the Boltzmann’ s constant, and T the absolute temperature, while and P1(υ ) are given by Eqs.  (5) and (6), respectively, with Δ i replaced by the Doppler-shift frequency detuning and ki is the wave vector of the i-th beam.

Let us consider the case in which the probe and coupling fields are counterpropagating. By setting k1 = − k1z and k2 = k2z, we have and , where ζ 2 = k2/k1 is the ratio between the magnitudes of the two wave vectors. Now, we express in Eq.  (8) as a function of v explicitly. In the case of ζ 2 ≠ 1, we have

Here,

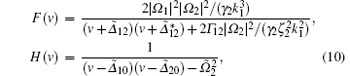
with , , , and . On the other hand, when ζ 2 = 1, we have

where

Now, let us consider the polarization, which according to Eq.  (6) can be expressed as . Here, the linear polarization is given by

with η = Nμ 1/k1 and . On the other hand, the nonlinear polarization for ζ 2 ≠ 1 is given by

While, for ζ 2 = 1 we have

2.3. Dressed-state model

Let us first consider the case of ζ 2 ≠ 1. We study the pole structure of H(ν ), which appears in Eqs.  (9) and (14). By solving the equation

we obtain

where

These poles are related to the resonance with the dressed state.[25] Physically, as a result of the Doppler frequency shift, the atoms with velocities ν ± will be in resonance with the dressed states, where ν ± are the real parts of ṽ ± . When ζ 2 < 1, the velocities ν + and ν − originate from the resonances of the dressed states | + 〉 and | − 〉 , respectively. By contrast, we have both ν + and ν − from the same dressed states when ζ 2 > 1.[25] One consequence is that there is a gap within which no ν ± exists when ζ 2 > 1. Now, we consider the case of ζ 2 = 1. According to Eqs.  (11) and (15) the poles of and appear at ṽ d. Here again, ṽ d corresponds to the transition to the dressed state.[24] Specifically, atoms with velocity ν d will be in resonance with the dressed state through Doppler frequency shift, where ν d is the real part of ṽ d. By contrast to the case of ζ 2 ≠ 1, there exists only one resonant velocity here.

Let us now consider the pole structure of the common factor F(ν ) appearing in Eqs.  (9) and (11). By solving

we obtain

Here,

This pole corresponds to the case that atoms are in resonance with the transition from | 1〉 to | 2〉 through Doppler frequency shift.

Now, we consider the pole structure of the nonlinear polarization 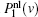. Comparing Eq.  (14) with Eq.  (9) for ζ 2 ≠ 1 and Eq.  (15) with Eq.  (11) for ζ 2 = 1, it is found that the poles ṽ 12 and originating from the factor F(ν ) in are replaced by ṽ 10, which corresponds to the transition from | 0〉 to | 1〉 . We note that the values of ṽ 10, ṽ 12, ṽ ± and ṽ d vary as we scan the probe beam, and the integral in Eq.  (8) consists mainly of the contributions of atoms with velocities corresponding to these poles.

3. Numerical results

In this section, we shall investigate the absorption and fluorescence excitation spectra in a Doppler-broadened system. For comparison, we first present the spectra in a homogeneously broadened system. Figure  2 presents the imaginary part of the polarization P1 and the population versus Δ 1 with Δ 2/Γ 10 = 0, Γ 20/Γ 10 = 0.1, and Ω 2/Γ 10 = 0.5 (solid curve), 2 (dashed curve), and 5 (dotted curve). For strong coupling field, both spectra exhibit AT splitting. The spectrum becomes different when the coupling field is weak. Specifically, the absorption spectrum shows a transparency window which is explained as the result of the Fano-type quantum interference (solid curve in Fig.  2(a)). By contrast, the window is absent in the fluorescence excitation spectrum (solid curve in Fig.  2(b)).

Fig.  2. (a) Imaginary part of P1 and (b) versus Δ 1 with Δ 2/Γ 10 = 0, Γ 20/Γ 10 = 0.1, and Ω 2/Γ 10 = 0.5 (solid curve), 2 (dashed curve), and 5 (dotted curve). The maxima of im[P1] in (a) and in (b) are normalized to 1.

Let us now consider a Doppler-broadened system with parameters Γ 10/k1u = 0.02 and Γ 20/Γ 10 = 0.1. Figures  3– 5 present the imaginary part of the polarization and the population versus Δ 1 with ζ 2 = 1.2, 1, and 0.8, respectively. The other parameters are Δ 2/Γ 10 = 0 and Ω 2/Γ 10 = 0.5 (solid curve), 2 (dashed curve), and 5 (dotted curve) for Figs.  3 and 4, and Ω 2/Γ 10 = 20 (solid curve), 50 (dashed curve), and 80 (dotted curve) for Fig.  5. These figures indicate that in a Doppler-broadened system the EIT resonance and AT splitting depend not only on the strength of the coupling field but also on the ratio between the magnitudes of the wave vectors ζ 2.

Fig.  3. (a) Imaginary part of and (b) versus Δ 1 with ζ 2 = 1.2, Δ 2/Γ 10 = 0, and Ω 2/Γ 10 = 0.5 (solid curve), 2 (dashed curve), and 5 (dotted curve). The maxima of im in (a) and in (b) are normalized to 1.
Fig.  4. (a) Imaginary part of and (b) versus Δ 1 with ζ 2 = 1, Δ 2/Γ 10 = 0, and Ω 2/Γ 10 = 0.5 (solid curve), 2 (dashed curve), and 5 (dotted curve). The maxima of im in panel (a) and in panel  (b) are normalized to 1.
Fig.  5. (a) Imaginary part of and (b) versus Δ 1 with ζ 2 = 0.8, Δ 2/Γ 10 = 0, and Ω 2/Γ 10 = 20 (solid curve), 50 (dashed curve), and 80 (dotted curve). The maxima of Im in panel  (a) and in panel  (b) are normalized to 1.

Let us first consider the case of ζ 2 = 1.2, as shown in Fig.  3. By contrast to the homogeneously broadened case, here both absorption and fluorescence excitation spectra exhibit window when the coupling field is weak (solid curves in Fig.  3). Furthermore, both spectra show similar characteristics of AT splitting. Specifically, corresponding to the case of fluorescence excitation spectra, there are two absorption peaks at the edges of the EIT window. The only difference between them is that the absorption spectrum has a Doppler-broadened background, while the fluorescence excitation spectrum is background-free.

The absorption spectrum behaves quite differently when ζ 2 = 1 (Fig.  4(a)). Although the transparency window is still Doppler-free, no doublet structure appears in the absorption spectrum. On the other hand, the fluorescence excitation spectrum shows a single peak when the coupling field is weak (solid curve in Fig.  4(b)). As the strength of coupling field increases, the spectrum becomes broader. In addition, a window appears at the center of the spectrum. The width of the window increases with the increase of the coupling field strength. Moreover, there is no indication of AT splitting in the fluorescence excitation spectrum.

Finally, let us consider the case of ζ 2 = 0.8 (Fig.  5). In general, both the absorption and fluorescence excitation spectra are similar to those in the homogeneously broadened system. For example, in the weak coupling field regime the absorption spectrum shows a transparency window, which does not appear in the fluorescence excitation spectrum; while in the strong coupling field regime, both spectra exhibit AT splitting. On the other hand, these spectra are no longer Doppler-free. Therefore, to obtain the doublet structure, a much higher coupling field is required.

4. Macroscopic effects in EIT resonance and fluorescence excitation spectrum

The wave-number-ration dependence of the absorption and fluorescence excitation spectra can be explained by the dressed-state model. The solid curves in Fig.  6 present the resonant velocities of the transitions from | 0〉 to the dressed states as a function of the frequency detuning Δ 1/Γ 10 with Δ 2/Γ 10 = 0, Ω 2/Γ 10 = 5, and ζ 2 = 1.2, 1, and ζ 3 = 0.8. We also present the resonant velocity of the transition from | 0〉 to the | 1〉 (dashed curves). Let us first consider the case of ζ 2 > 1. According to Eq.  (18) there is no solution for ν ± in the regime , leading to a gap shown in Fig.  6(a). The gap is given by in the case of Δ 2 = 0. Now, we consider the case of ζ 2 = 1 (Fig.  6(b)). In this case, there is only one resonant velocity ν d, which approaches ± ∞ as Δ 1+ Δ 2 → 0 (see Eq.  (12)). Finally, ν ± exists for any value of Δ 1 when ζ 2 < 1 as shown in Fig.  6(c).

Fig.  6. Resonant velocities of the transitions from | 0〉 to the dressed states (solid curve) and ν 10/u (dotted curve) versus Δ 1/Γ 10 with Δ 2/Γ 10 = 0, Ω 2/Γ 10 = 5, and (a) ζ 2 = 1.2, (b) ζ 2 = 1, and (c) ζ 3 = 0.8.

In a Doppler-broadened system, although the total population and polarization are given by the integration over the whole velocity distribution, the main contributions originate from the atoms with resonant velocities, shown as poles of P1(ν ) and . There are two types of poles, i.e., ṽ ± and ṽ d, corresponding to the transition from | 0〉 to the dressed states, and ṽ 10 and ṽ 12, corresponding to the resonant transitions from | 0〉 to | 1〉 and | 1〉 to | 2〉 , respectively. Since the atoms are initially on the state | 0〉 , the contribution from the pole ṽ 12 can usually be neglected. Figures  7 and 8 present the velocity dependence of the eigenenergy of the lower dressed state ɛ − , the imaginary part of , and the population with Ω 2/Γ 10 = 5 and Δ 2/Γ 10 = 0, for ζ 2 = 1.2, and ζ 2 = 1, respectively. In Fig.  7, Δ 1/Γ 10 = 3 (solid curve), 3.7 (dashed curve), 4 (dotted curve), and 5 (dash-dotted curve); in Fig.  8, Δ 1/Γ 10 = 0 (solid curve), 1 (dashed curve), 2 (dotted curve), and 4 (dash-dotted curve). The resonant velocities correspond to the crossing points of the curves ɛ − (ν ) with the line y = 0 (thin solid lines in Figs.  7(a) and 8(a)). As shown in the figures, the main difference between Im and is that for the former case, there exists contribution from the pole which can lead to the stimulated emission of a photon at the frequency of the probe beam, thus inducing destructive polarization interference between two types of poles.

Fig.  7. Velocity dependence of (a) ɛ − , (b) imaginary part of , and (c) with ζ 2 = 1.2, Ω 2/Γ 10 = 5, Δ 2/Γ 10 = 0, and Δ 1/Γ 10 = 3 (solid curve), 3.7 (dashed curve), 4 (dotted curve), and 5 (dash-dotted curve). The resonant velocities ν ± correspond to the crossing points of the curves ɛ − (ν ) with a line y = 0 (thin solid line) shown in panel (a). In panel (b) the maximum of Im with Δ 1/Γ 10 = 5 is normalized to 1; while in panel (c) the maximum of with Δ 1/Γ 10 = 4 is normalized to 1.
Fig.  8. Velocity dependence of (a) ɛ − , (b) imaginary part of , and (c) with ζ 2 = 1, Ω 2/Γ 10 = 5, Δ 2/Γ 10 = 0, and Δ 1/Γ 10 = 0 (solid curve), 1 (dashed curve), 2 (dotted curve), and 4 (dash-dotted curve). The resonant velocity ν d corresponds to the crossing points of the curves ɛ − (ν ) with a line y = 0 (thin solid line) shown in panel (a). In panel (b) the maximum of Im with Δ 1/Γ 10 = 4 is normalized to 1; while in panel (c) the maximum of with Δ 1/Γ 10 = 2 is normalized to 1.

Let us consider the case of ζ 2 > 1. We first analyze the resonant condition for and Im. Due to the presence of the factor H(ν ) in the integration (8), the resonance occurs as ν + = ν − (see Eq.  (17)). Accordingly, from Eq.  (18) we obtain the resonant frequency . Based on this characteristics, the absorption and fluorescence excitation spectra shown in Fig.  3 can be understood. First, the windows in both spectra correspond to the gap where no ν ± exists. The amplitudes of Im and then increase sharply as Δ 1 is tuned to the resonant frequency (dashed curve in Figs.  7(b) and 7(c)). Since ɛ − (ν ) is relatively flat near the point ν = ν + = ν − (dashed curve in Fig.  7(a)), atoms in a relatively wide region of velocity will contribute to the signal. After that, the signals decrease as Δ 1 is detuned so that the separation between ν + and ν − increases. Here, we see two peaks in the velocity dependence of Im and corresponding to the poles ṽ ± and ṽ − . Now, we discuss the role of the pole at ṽ 10 in the nonlinear polarization given by Eq.  (14), which induces amplification of the probe beam. Within the gap, since no atom can be in resonance with the dressed state the stimulated emission of photons will suppress the linear absorption, leading to a transparent window in the Doppler profile. The amplitude of Im then increases sharply as Δ 1 is tuned to the resonant frequency .

Comparing Figs.  6(a) and 6(b), the main difference between the cases of ζ 2 > 1 and ζ 2 = 1 is that the Δ 1 dependence of the resonant velocity exhibits no gap for the later case. Let us first analyze the absorption spectrum when ζ 2 = 1. As shown in Fig.  8(b), when Δ 1/Γ 10 = 0, no atom in the Doppler profile can be in resonance with the dressed state. On the other hand, due to the pole at ṽ 10, Im exhibits a single dip (solid curve), thus inducing transparency in the absorption spectrum. As Δ 1 is tuned away from the resonance, atoms with velocity ν d will be in resonance with one of the dressed states. As a result, the destructive interference between contributions from the poles ṽ 10 and ṽ d causes the signal of Im to decrease. Finally, when Δ 1 is far away from the resonance we have vd ≃ v10 (see Fig.  6(b)), leading to almost complete cancellation of the contributions from the two poles (dash-dotted curve in Fig.  8(b)). Comparing to the case of ζ 2 > 1, since no gap appears in the Δ 1 dependence of the resonant velocity, the spectrum of ζ 2 = 1 exhibits no absorption peaks corresponding to the AT splitting.

Now, let us consider the fluorescence excitation spectrum. First, is small when Δ 1/Γ 10 ≃ 0 (solid curve in Fig.  8(c)) because no atom in the Doppler profile can be in resonance with the dressed state. The pole ṽ d then makes contribution to the population as Δ 1 is detuned so that the resonant velocity ν d is within the Doppler profile. Now, we examine the velocity dependence of the eigenenergy ɛ − shown in Fig.  8(a). The slope of ɛ − (ν ) at ν = ν d, which corresponds to the crossing point of the curve ɛ − (ν ) with the line y = 0, is relatively flat when the detuning Δ 1 is small (dashed curve). In this case atoms in a relatively wide region of velocity will contribute to the signal (dashed curve in Fig.  8(c)). The slope at ν = ν d becomes sharp as Δ 1 is tuned far away from the resonance (dash-dotted curve in Fig.  8(a)), causing the narrower velocity region of the involved atoms (dash-dotted curve in Fig.  8(c)). Another important thing is that, as shown in Fig.  6(b), ν d approaches the center of the Doppler profile as | Δ 1| increases. As a result, we see the maximum of Im increases as Δ 1 is moved away from the resonance (dash-dotted curve in Fig.  8(b)). However, for the population we actually see the decline of the maximum of (dash-dotted curve in Fig.  8(c)). This is due to the factor in Eq.  (11). With these characteristics the fluorescence excitation spectrum with Ω 2/Γ 10 = 5 (dotted curve in Fig.  4(b)) can then be understood. We should emphasize that although this spectrum exhibits a similar doublet structure, it is nothing to do with the AT splitting. Furthermore, the two peaks can be overlapped for small Ω 2, leading to the disappearance of the doublet structure (solid curve in Fig.  4(b)).

Finally, the absorption and fluorescence excitation spectra are relatively easy to understand for the case of ζ 2 < 1 (Fig.  5). Since within the Doppler profile there are always atoms of velocities ν = ν + and ν = ν − which are in resonance with the dressed state, as shown in Fig.  6(c), the spectrum exhibits a characteristic of Doppler broadening.

5. Discussion and conclusion

Traditionally, EIT is explained as the result of quantum Fano interference. The requirement for this explanation is based on the fact that when the coupling field is very weak so the AT doublet structure becomes overlapped, a sharp transmission window is still observable. One way to clarify the role of quantum interference is to compare the absorption spectrum with the fluorescence excitation spectrum. For the homogeneously broadened case, both spectra exhibit AT splitting when the strong coupling field is strong. However, when the coupling field is weak the absorption spectrum shows a sharp window, which is absent in the fluorescence excitation spectrum (Fig.  2). Now, let us consider the Doppler-broadened system. Although the absorption spectrum depends strongly on the wave-number ratio ζ 2, the transparency window exists in all cases (Figs.  3(a), 4(a), 5(a)). It may imply that the quantum interference plays a similar role to that in the case of homogeneously broadened system. However, by comparing the fluorescence excitation spectra in the Doppler-broadened system with those in the homogeneously broadened system, it is found that for the former case, instead of quantum interference, here the macroscopic effect plays a more crucial role. Specifically, for the case of ζ 2 > 1 (Fig.  3) both absorption and fluorescence excitation spectra show window when the coupling field is weak. This window is related to the existence of a gap within which no atoms can be in resonance with the dressed states through Doppler frequency shifting (Fig.  6(a)). Similar to the case of ζ 2 > 1, the transparency window in the case of ζ 2 = 1 (Fig.  4(a)) is due to fact that ν d approaches ± ∞ as Δ 1→ 0, so no atoms in the Doppler profile can be in resonance with the dressed state (Fig.  6(b)). On the other hand, no gap exists in this case. As a result, we see no indication of AT splitting in both the absorption and the fluorescence excitation spectra when ζ 2 = 1.

In conclusion, we have studied the relationship between the EIT resonance and the AT splitting in a cascade three-level Doppler-broadened system, and have pointed out the importance of the polarization interference in the Doppler-broadened system. Previously, we have studied resonant stimulated Raman gain and loss spectroscopy in the varLambda-type three-level system and found that in the presence of a coupling field the probe beam can exhibit either gain or loss, depending on the frequencies of the incident beams.[24] In the cascaded three-level system, the gain originates from the stimulated emission due to the scattering of the coupling field by the two-photon coherence. By contrast, the loss is due to the transition from the ground state to the dressed state. In a Doppler-broadened system, gain and loss can exist simultaneously, resulting in destructive polarization interference between atoms of different velocities, as shown in Figs.  7(b) and 8(b). Here, when we use the absorption spectrum instead of the fluorescence excitation spectrum to detect the AT splitting, the two phenomena of EIT and AT splitting can be explained within the same framework.

Reference
1 Harris S E, Field J E and Imamoglu A 1990 Phys. Rev. Lett. 64 1107 DOI:10.1103/PhysRevLett.64.1107 [Cited within:1]
2 Fleischhauer M, Imamoglu A and Marangos J P 2005 Rev. Mod. Phys. 77 633 DOI:10.1103/RevModPhys.77.633 [Cited within:1]
3 Kang H and Zhu Y 2003 Phys. Rev. Lett. 91 093601 DOI:10.1103/PhysRevLett.91.093601 [Cited within:1]
4 Wang H, Goorskey D and Xiao M 2001 Phys. Rev. Lett. 87 073601 DOI:10.1103/PhysRevLett.87.073601 [Cited within:1]
5 Kash M M, Sautenkov V A, Zibrov A S, Hollberg L, Welch G R, Lukin M D, Rostovtsev Y, Fry E S and Scully M O 1999 Phys. Rev. Lett. 82 5229 DOI:10.1103/PhysRevLett.82.5229 [Cited within:1]
6 Deng L and Payne M G 2003 Phys. Rev. Lett. 91 243902 DOI:10.1103/PhysRevLett.91.243902 [Cited within:1]
7 Zuo Z, Sun J, Liu X, Jiang Q, Fu G, Wu L A and Fu P 2006 Phys. Rev. Lett. 97 193904 DOI:10.1103/PhysRevLett.97.193904 [Cited within:1]
8 Niu J, Wang R, Wu L A and Fu P 2009 Opt. Soc. Am. B 26 2268 DOI:10.1364/JOSAB.26.002268 [Cited within:1]
9 Niu J, Wang R, Wang B, Wu L A and Fu P 2009 J. Phys. B 42 175505 DOI:10.1088/0953-4075/42/17/175505 [Cited within:1]
10 Fleischhauer M and Lukin M D 2000 Phys. Rev. Lett. 84 5094 DOI:10.1103/PhysRevLett.84.5094 [Cited within:1]
11 Liu C, Dutton Z, Behroozi C H and Hau L V 2001 Nature 409 490 DOI:10.1038/35054017 [Cited within:1]
12 Autler S H and Townes C H 1955 Phys. Rev. 100 703 DOI:10.1103/PhysRev.100.703 [Cited within:1]
13 Anisimov P and Kocharovskaya O 2008 J. Mod. Opt. 55 3159 DOI:10.1080/09500340802302378 [Cited within:1]
14 Abi-Salloum T Y 2010 Phys. Rev. A 81 053836 DOI:10.1103/PhysRevA.81.053836 [Cited within:1]
15 Anisimov P M, Dowling J P and Sand ers B C 2011 Phys. Rev. Lett. 107 163604 DOI:10.1103/PhysRevLett.107.163604 [Cited within:1]
16 Giner L, Veissier L, Sparkes B, Sheremet A S, Nicolas A, Mishina O S, Scherman M, Burks S, Shomroni I, Kupriyanov D V, Lam P K, Giacobino E and Laurat J 2013 Phys. Rev. A 87 013823 DOI:10.1103/PhysRevA.87.013823 [Cited within:1]
17 Gea-Banacloche J, Li Y Q, Jin S Z and Xiao M 1995 Phys. Rev. A 51 576 DOI:10.1103/PhysRevA.51.576 [Cited within:1]
18 Shepherd S, Fulton D J and Dunn M H 1996 Phys. Rev. A 54 5394 DOI:10.1103/PhysRevA.54.5394 [Cited within:1]
19 Javan A, Kocharovskaya O, Lee H and Scully M O 2002 Phys. Rev. 66 013805 DOI:10.1103/PhysRevA.66.013805 [Cited within:1]
20 Lee H, Rostovtsev Y, Bednar C J and Javan A 2003 Appl. Phys. B 76 33 [Cited within:1]
21 Iftiquar S M, Karve G R and Natarajan V 2008 Phys. Rev. A 77 063807 DOI:10.1103/PhysRevA.77.063807 [Cited within:1]
22 Ahmed E and Lyyra A M 2007 Phys. Rev. A 76 053407 DOI:10.1103/PhysRevA.76.053407 [Cited within:2]
23 Lazoudis A, Ahmed E H, Li L, Kirova T, Qi P, Hansson A, Magnes J and Lyyra A M 2008 Phys. Rev. A 78 043405 DOI:10.1103/PhysRevA.78.043405 [Cited within:1]
24 Pei L, Lu X, Bai J, Miao X, Wang R, Wu L A, Ren S, Jiao Z, Zhu H, Fu P and Zuo Z 2013 Phys. Rev. A 87 063822 DOI:10.1103/PhysRevA.87.063822 [Cited within:2]
25 Niu J, Pei L, Lu X, Wang R, Wu L A and Fu P 2011 Phys. Rev. A 84 033853 DOI:10.1103/PhysRevA.84.033853 [Cited within:2]