†Corresponding author. E-mail: ghanbari@phys.ui.ac.ir
The first-order correct-boundary Coulomb–Born distorted-wave approximation is used to study the double-electron capture by protons from the ground-state helium atoms at intermediate and high impact energies. The differential double capture cross sections are obtained as a function of the projectile scattering angle and the total cross sections as a function of the impact energy. In the considered range of impact energy, our calculation shows that although the results are not so sensitive to the static inter-electronic correlations in the initial channel, the strong final-state correlations have a large effect on the magnitudes of the double capture cross sections. The calculated differential and integral cross sections are compared with their available experimental values. The comparison shows a good agreement between the present calculations and the measurements. The comparison of the integral cross sections shows that the present approach is compatible with other theories.
The singly charged negative hydrogen ion H− is one of the simplest two-electron systems. It has a great number of practical and theoretical applications in many fields of science and technology.[1] For example, it plays an important role in the opacity of stellar atmospheres.[2] It also plays a fundamental role in the absorption and emission of partially ionized hydrogen plasmas.[3] The fact that the negative hydrogen ion can be used as an efficient antioxidant in the human body expands the scope of its applications to biology; however, injection of negative hydrogen ions into high energy accelerators is one of its main applications.[4] Moreover, it can be used for the production of neutral beams of energetic hydrogen atoms for fusion devices.[5]
From the theoretical viewpoint, the exact energy levels and analytical wave functions are not available for two-electron bound systems. The negative atomic hydrogen ion has only two bound states, the ground 1s2 (1S) state and the doubly excited 2p2 (3P) state. The latter was predicted computationally but has not been observed till date.[1] Consequently, the accurate approximate solution for the ground-state energy and wave functions of the negative hydrogen ion may be used to examine the validity of the theoretical models that are outlined to describe the dynamics of the two-electron systems and their extensions to more complicated systems.[6] It is also a proper basic candidate for the study of the inter-electronic correlations existing among the electrons in multi-electron atoms.[7]
One way to produce negative hydrogen ions is through collisions between protons and helium atoms to exchange both of the involved electrons. Such a collision process is a pure four-body problem, which provides a stringent test of the approximation methods used in the analysis of the dynamic of the four-body collision process. A large number of experimental measurements of the double-capture (DC) total cross sections (TCSs) have been reported in the literature for this process.[8– 11] The DC TCSs have also been theoretically calculated using various theoretical models. For example, the integral cross section for the capture of two electrons by protons in helium was calculated using the first-Born approximation by Gerasimenko.[12] The TCSs for the formation of H− by double charge exchange in fast proton-helium collisions were investigated using the atomic orbital expansion (AOE) method, [13] the four-body continuum distorted wave (CDW-4B) approximation, [14] and the boundary-corrected four-body first-Born (CB1-4B) theory.[15] For an extensive review of these models, the readers are referred to Refs. [7] and [16].
Although a significant progress has been made in studying the specified collision process, [7, 16] most of the theoretical as well as the experimental studies were devoted to the TCSs, while differential cross sections (DCSs) give more detailed information of the collision dynamics. Recently, the differential double capture cross sections for 15– 150 keV proton– helium collisions were measured by Schulz et al.[17] However, to the best of our knowledge, no theoretical differential calculation was reported for this collision process. In consequence, we are motivated to calculate the DC DCSs for this process.
Recently, we have developed a theoretical three-body approach based on the Coulomb– Born distorted-wave (CBDW) approximation[18– 20] to study the single capture (SC) process in various energetic ion– atom collisions.[21– 24] For most of the cases considered, the calculated results are in satisfactory agreement with the available experimental data at moderate and high impact energies for which a first-order perturbation theory is valid. In a further study, the three-body CBDW approximation was generalized to its four-body version and applied to single and double capture processes.[25– 29] In this paper, in continuation of our previous studies, we employ the post and prior forms of the four-body correct-boundary Coulomb– Born distorted-wave (CBDW-4B) approximation to investigate the DC process in energetic proton– helium collisions. Various approximate initial and final bound-state wave functions are used to explore the influence of the static electronic correlations on the rearrangement process. The results are compared with other theoretical results and the corresponding experimental values.
The organization of this paper is as follows. In Section 2, the theoretical formalism is outlined and the reduced two-dimensional integral forms of the prior and post amplitudes are derived. The obtained results for differential and integral cross sections and their related comparisons and discussion are given in Section 3. Finally, a summary is given in Section 4. Atomic units will be used throughout unless stated otherwise.
A four-body collision is considered in which a projectile ion P is incident on a bound subsystem consisting of two active electrons e1, e2 and a target ion T. The charges of the projectile and the target ions are denoted by ZP = 1 and ZT = 2, respectively. Their masses are MP and MT, respectively. Let the position vectors of the two electrons with respect to the target nucleus T and the projectile P be denoted by r1T, r2T and r1P, r2P, respectively. Assume both electrons are captured by the projectile ion during the collision process. Let Ri be the position vector of the projectile with respect to the center of mass of the target atom and Rf be that of the target ion with respect to the center of mass of the newly-formed negative ion. Finally, we denote the position vector of P relative to T by R and the position vector of e2 relative to e1 by r12, then r12 = r2T − r1T = r2P − r1P.
The total Hamiltonian of the entire system, H, in the center of mass coordinate system corresponding to the initial and the final channels, respectively, may be written as
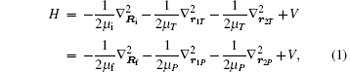
where the potential energy V is given by
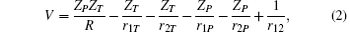
and the reduced masses associated with the relative coordinates are
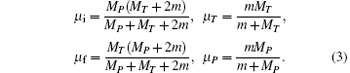
It is possible to split the total Hamiltonian H into the prior form H = Hi + Vi for the initial channel and into the post form H = Hf + Vf for the final channel. The perturbation potentials in the entrance and the exit channels can be written as
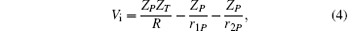
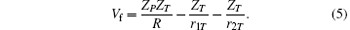
For the specified rearrangement process, the asymptotic forms of these potentials, 
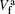
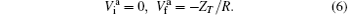
As can be seen, a residual interaction exists in the final channel due to the long-range nature of the Coulomb interaction. This residual interaction distorts the scattered waves even at very far distances from the scattering center. Therefore, it is necessary to modify the standard T-matrix formalism by including the distortion produced by this residual Coulomb potential. This distortion is included in the Coulomb– Born distorted-wave approximation to satisfy the correct Coulomb boundary conditions. In the four-body boundary-corrected first-order Coulomb– Born distorted-wave approximation, the prior and post forms of the transition amplitude for a double-electron capture process in the specified collision system are respectively given by
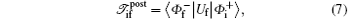
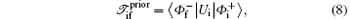
where 
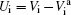
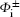
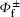
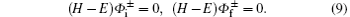
For the considered reaction, these solutions are
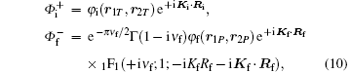
where ν f = – μ fZT/Kf is the final Sommerfeld parameter, Ki and Kf are the initial and the final wave vectors for the relative motion in the center of mass frame, φ i(r1T, r2T) and φ f(r1P, r2P) are the bound-state wave functions of the initial target atom and the produced negative ion in the final channel, and 1F1(a; b; x) and Γ (x) are respectively the confluent hypergeometric function and Euler’ s gamma function.
Inserting explicit forms of the wave functions and the modified perturbation potentials into Eqs. (7) and (8) leads to
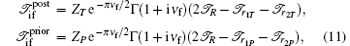
where
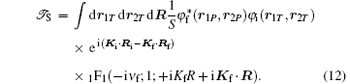
For computational purposes, we assume that the initial and the final bound-state wave functions are given by
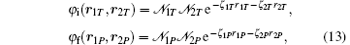
where 𝒩 1T, 𝒩 2T, 𝒩 1P, and 𝒩 2P are the normalization constants, and ζ 1T, ζ 2T, ζ 1P, and ζ 2P are the zeta parameters whose values are known for the chosen wave functions.
Substituting the given bound-state wave functions in Eq. (12) and performing some manipulations, we reduce the partial amplitude IS to

in which we have used the relation
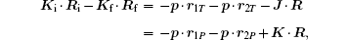
where the wave vectors J, K, and p are respectively the momenta transferred to the projectile ion P, the target ion T, and each of the electrons e1 and e2. The momentum conservation for this process takes the form J + K + 2p = 0. When terms of order 1/MP are neglected, this relation reduces to J + K + 2υ = 0, where υ is the velocity of the incident particle.
The nine-dimensional integrals for the partial matrix elements can be reduced to two-dimensional integrals using analytical manipulations. To this end, we consider a general integral
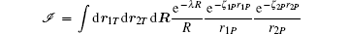
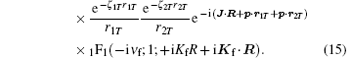
Using the inverse Fourier transform of the terms involving r1P and r2P according to
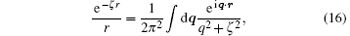
employing the equations r1P = r1T – R, r2P = r2T − R, and performing some manipulations, we deduce
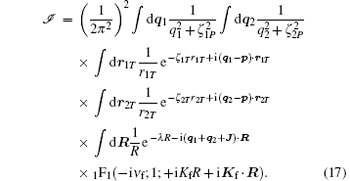
The integrations over r1T and r2T can be carried out using the integral identity
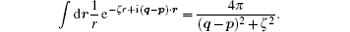
In consequence, we have
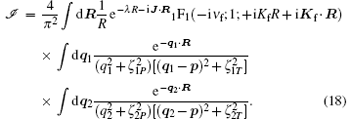
Using the Feynman identity[30]
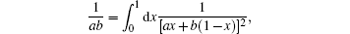
we have
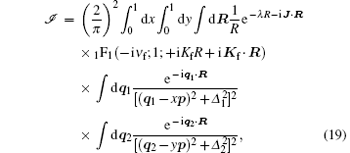
where
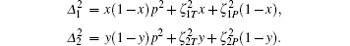
The integrals over q1 and q2 can be evaluated using the following identity:
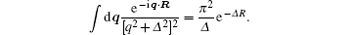
Inserting the results in Eq. (19), we have
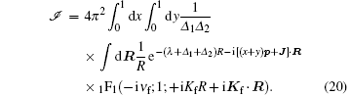
The R integral is a special case of the Nordsieck integral[31] and can be performed analytically. The result is
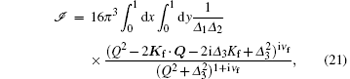
where
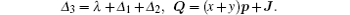
Subsequently, we have
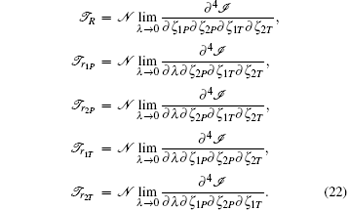
Our results show that the agreement between the differential and the integral cross sections obtained from the post form of the transition amplitude with experiment is better than that obtained from the prior form. Therefore, in the following discussion, the post results would be preferred. In the laboratory frame, from the post form of the transition amplitude, the double-electron capture differential and integral cross sections are respectively given by
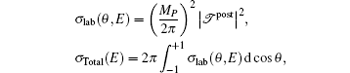
where θ is the scattering angle in the specified frame.
In this section, the calculated differential and total cross sections for the formation of negative hydrogen ions in fast proton– helium collisions are presented and discussed. In order to analyze the influence of the static electronic correlation on the dynamic of the considered reaction, we examine different wave functions for the helium target and the formed negative ion.
The two different wave functions considered for the ground-state helium atoms are i) the one-parameter Hylleraas wave function[32]
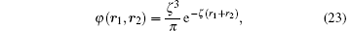
with ζ = ZT − 5/16 = 27/16, and ii) the highly correlated multi-parameter Byron– Joachain[33] wave function
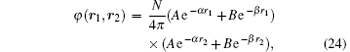
where the normalization constant N is given by N = 4/[A2/α 3 + B2/β 3 + 16AB/(α + β )3]. Here, A = 2.60505, B = 2.08144, α = 1.41, and β = 2.61, consequently N = 1.
We also use three different wave functions for the ground state of the H− ion: i) the one-parameter Hylleraas wave function[32] given by Eq. (23) with ζ = ZP − 5/16 = 11/16; ii) the two-parameter bound-state wave function given by Shingal et al.[34]

where the introduced constant parameters are α = 1.0312, β = 0.23537, and 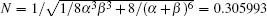
Figure 1 displays the variation of the double-electron capture cross sections as a function of the projectile scattering angle at incident projectile energies of 15 keV, 25 keV, 40 keV, 50 keV, 75 keV, 100 keV, 125 keV, and 150 keV. These results are obtained by using the post form of the CBDW-4B theory. The cross sections are evaluated by using the uncorrelated one-parameter Hylleraas wave function for the ground-state helium targets, while the above mentioned three different wave functions are used to describe the produced hydrogen negative ions in their ground states. All three sets of results show a quite broad structure which is located at more forward angles. This structure which occurs in the forward-peak region is called the kinematic peak. The results are compared with the experimental values from Schulz et al.[17]
 | Fig. 1. Angular distributions of the double-electron capture differential cross sections for the collision of fast protons with helium atoms in their ground states. Both cross sections and scattering angles are given in the laboratory frame. The initial bound-state wave function for the helium atoms is the one-parameter Hylleraas wave function, while the final state wave function for the produced negative ion is described by the Shingal et al.[34] (solid lines), the Lö wdin[35] (dashed lines), and the Hylleraas[32] (dash-dotted lines) wave functions. Closed circles are results from experiments.[17] The incident projectile energies are (a) 15 keV, (b) 25 keV, (c) 40 keV, (d) 50 keV, (e) 75 keV, (f) 100 keV, (g) 125 keV, and (h) 150 keV. |
At the lower impact energy of 15 keV, the results deviate away from the experiments. This is reasonable, because the perturbation methods are not so valid for the lower impact energies. At the impact energy of 25 keV, the results obtained using the Shingal wave function are in excellent agreement with the experiments, while the results of the other two wave functions, which show an unphysical structure in the DCSs, give poor agreement with the measurements. The mentioned structure is due to the mutual cancelation occurring between the repulsive and the attractive matrix elements in the post CBDW-4B amplitude. As the incident energy increases, this structure also appears in the results of the Shingal wave function. However, at higher impact energies, this structure gradually becomes smoother, and even disappears in the results of the Lö wdin wave function.
As shown in Fig. 1, the DCSs for this process are very sensitive to the choice of the final wave function. In other words, the strong final-state electron correlation effects play a very important role in the DC dynamics of the fast proton– helium collisions. For moderate impact energies between 25 keV and 100 keV, the Shingal wave function provides a good description of these effects, especially in the forward-peak region and at the larger scattering angles. As the incident energy increases, a discrepancy appears between these results and the measurements at the forward-peak region. This discrepancy is found to increase with increasing incident energy. However, the proximity of the results to their experimental values remains satisfactory. Although, the present theory with the Shingal wave function is successful in fitting the experimental data in forward-peak and large-angle scattering regions at moderate incident energies, it does not give the correct behavior of cross sections in the angular region where the unphysical structure appears.
Despite the fact that the static electron correlations in the exit channel play a significant role in the specified double capture process, the initial-state electron correlations play a minor role in the process at the considered impact energies. In order to investigate this issue, calculations have been iterated by using the Byron– Joachain wave function[33] for the initial state of helium targets. It is found that the iterated calculations reproduce the previous results shown in Fig. 1 with some marginal differences. For example, figure 2 compares the 25 keV results obtained using the Byron– Joachain wave function for the helium atoms with those obtained previously using the Hylleraas wave function. It is assumed that the final bound state is described by the Shingal wave function. As can be seen, the different wave functions of the target atom lead to the same behavior for the DC differential cross section. This indicates that even on the differential level, the double capture is essentially an uncorrelated process in this energy range. Also as can be seen, the agreement of the theoretical results with the measurements is excellent.
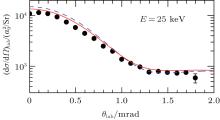 | Fig. 2. Comparison of the results obtained using different wave functions for the helium targets: Byron– Joachain (solid line) and Hylleraas (dashed line) wave functions. Closed circles are from measurements.[17] In both cases, the final state is described by using the wave function given by Shingal et al.[34] |
In Fig. 3, the calculated TCSs for the formation of H− as a function of the incident proton energy are presented. For comparison, the experimental findings[8– 11] and the previous theoretical results[13– 15] are also depicted in this figure. The present results are obtained by using the Hylleraas wave function for the initial bound state and the wave function given by Shingal et al. for the final one. As is expected for lower scattering energies, the perturbation CBDW-4B, CDW-4B, and CB1-4B theories considerably overestimate the measured data. However, for these energies, the present calculations are closer to the experimental findings. For intermediate energies between 20 keV and 100 keV, the present calculations are in excellent agreement with the available experimental data. This is due to the fact that the main contribution to the integral cross sections comes from the forward scattering of the newly formed hydrogen ion, and the present calculation gives a good description of the differential cross sections at forward-peak scattering angles. At impact energies higher than 100 keV, although the cross sections of the CDW-4B method are in excellent agreement with the available experimental data, the deviation of the present predictions from the experimental values gradually becomes considerable with increasing incident energy. There exist some noticeable differences between the present results and the CB1-4B ones showing that the present theory is in better agreement with the measured data. The cross sections of the atomic orbital expansion method[13] underestimate the measured data at energies lower than 50 keV, while the pattern is reversed at energies above 100 keV. In fact, the experimental cross section for the process of interest is very small, attaining a maximum value of around 2 10− 2 a.u. at the collision energy of about 30– 40 keV, whereas the cross sections for excitation and ionization are much larger. Therefore, since ionization and charge transfer to the continuum of H− are strongly coupled, first-order methods are unlikely to be reliable for energies above 100 keV.
The double-electron capture process by impact of energetic protons on the helium atoms in their ground states has been studied using the CBDW-4B approximation. The calculations have been performed using various wave functions for the initial and the final bound states of the helium target and the formed negative hydrogen ion. Calculations show that the initial state correlations play a minor role in the process while the role of the final state correlations is fundamental. The influence of the strong final state correlations on the process causes considerable differences between the DCSs obtained using different final wave functions. In general, the agreement between the DCSs obtained using the final wave function given by Shingal et al. and their experimental values is better than that obtained using other considered wave functions. At moderate and higher impact energies, the results show a kinematical peak at extreme forward angles, which is followed by an unphysical structure in the angular distribution of the DCSs. At moderate impact energies, the agreement of the results and the measurements in the forward-peak region is reasonable. At scattering angles beyond the angular region in which the unphysical structure occurs, the agreement is still good. TCSs obtained from the present theory are in excellent agreement with measurements at impact energies between 20 keV and 100 keV. For higher energies, the present results are compatible with the CDW-4B ones and are better than those of the CB1-4B approximation.
One of the authors, HG, wishes to acknowledge the office of graduate studies at the University of Isfahan for their support and research facilities.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|



