Attosecond pulses can trace the ultrafast electronic dynamics in atoms and molecules with high accuracy, which has been a forefront subject that attracts much attention in science and technology.^{[1– 5]} Since high harmonic spectrum presents plateau area which is distributed regularly with equal frequencies, which makes it become first choice to produce attosecond light.^{[6– 8]} A typical description of HHG spectrum presents a sharp decrease in the initial harmonics, then the spectrum shows a plateau where all the harmonics have a similar amplitude, and finally a cutoff at the energy I_p + 3.17U_p. Here, I_p is the atomic ionization potential, and U_p is the ponderomotive energy which only depends on the laser parameters. The essence of HHG process can be described by the semiclassical three-step model.^{[9– 11]} First, the free electrons tunnel from the ground state to continuous states by tunneling or multi-photon ionization. Second, the electrons are then accelerated by a strong oscillating laser field. Finally, the electrons recombine with the parent ion and emit photons. There are many techniques for the generation of attosecond pulses, such as scheme of a single-cycle pulse, ^[12] a few-cycle laser field, ^{[13– 15]} double optical gating, ^[16] and multicycle driving laser field directly from an amplifier.^[17] By applying these techniques, isolated ultrashort XUV pulses have been obtained by several laboratories worldwidely.^{[18, 19]} Recently, Luo et al.^[20] have shown dramatic cutoff extension and broadband supercontinuum generation in multi-cycle two-color pulses, which can directly generate an isolated sub-100-as pulse. Hu et al.^[21] proposed effect of electron correlation on high-order harmonic generation of He model atom. Li et al.^[22] theoretically achieved an isolated 26-as pulse of He⁺ by means of an intense few-cycle chirped laser field. Recently, a scheme have been used to generate an isolated attosecond pulse by using a Terahertz (THz) field, which attracts much attention due to its potential applications.^{[23– 26]}

In this paper, we will produce an isolated ultrashort attosecond laser pulse by controlling the short and long trajectories in a 800-nm fundamental laser field combined with a THz field. The high-order harmonic generation (HHG) can be obtained by solving the time-dependent Schrö dinger equation (TDSE) accurately with time-dependent generalized pseudospectral (TDGPS) method.^{[27, 28]} The result shows that the plateau of high-order harmonics can be extended largely in the combined laser field. With such a spectrum, the generation of isolated attosecond pulses would be obtained straightforward, the shortest of which is 133  as.

The TDSE for H atom can be written as (in atomic units)

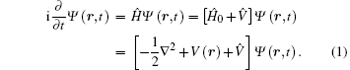
Here, Ĥ ₀ is the unperturbed Hamiltonian of H atom, and is the potential energy of H atom in an intense laser field, which is given by

The TDSE can be solved accurately and efficiently by the TDGPS method.^{[27, 28]} This method has two key steps. (i) The spatial coordinates are optimally discretized by pseudospectral discretization, which allows us to obtain denser grids near the nuclear origin, leading to more accurate initial wavefunction by using smaller number of grid points. (ii) A second-order split-operator technique in the energy representation is used for the efficient and accurate three-step time propagation of the wave function, which is given by

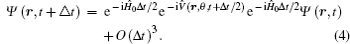
Once the time-dependent wave function is determined, we can compute the expectation value of the induced dipole moment in the acceleration form:

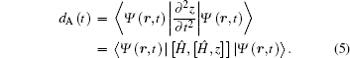
The corresponding HHG power spectrum can be obtained by Fourier transformation of the time-dependent dipole moment

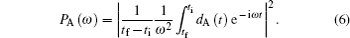
The attosecond pulse can be calculated by superposing several harmonics as follows:

where a_q = ∫ d (t) e^{− iqω t} dt. To study the detailed spectral and temporal structures of HHG, we perform time-frequency analysis by means of the wavelet transform,

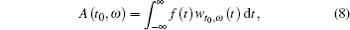
where w_{t0, ω} (t) is the wavelet transform kernel. It can be shown as follows:

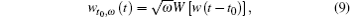
where is the Morlet wavelet.

In our calculation, a 800-nm fundamental laser field only and a 800-nm fundamental laser field combined with a THz field can be expressed as follows:

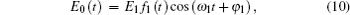
Here, E₁ = 0.10676  a.u. and E_THz = 0.01947  a.u. are the electric-field amplitudes, f₁ (t) and f_THz (t) are the Gaussian envelopes, ω ₁ = 0.0569  a.u. (λ = 800  nm) and ω _THz = 0.00949  a.u. (62.5  THz) are the frequencies, φ ₁ = 0.25π is the carrier-envelope phase (CEP), the durations of the Gaussian pulses are 5  fs and 16.022  fs, respectively. In our calculation, we use N = 1200 radial grid points and partial wave L = 120, the total time duration T = 16T₀, where T₀ = 2π /ω ₁. Figure  1(a) shows E₀(t) and E_c(t) as functions of time, respectively. Figure  1(b) presents the acceleration-form power spectra of H atom in fundamental field and combined field, respectively. From Fig.  1(b) we can see the HHG spectrum in the 800-nm fundamental laser field has a cutoff of 60^th order. When a THz field is added, it can be apparently seen that the plateau in the combined fields is extended to about 95^th order.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. (a) A 800-nm fundamental laser field only (black dotted curve) and a 800-nm fundamental laser field combined with a THz field (red solid curve). (b) The corresponding acceleration form power spectra in a 800-nm fundamental laser field only and a 800-nm fundamental laser field combined with a THz field, respectively.

Since HHG is very sensitive to ionization probability, the corresponding ionization probability in a 800-nm fundamental laser field only and a 800-nm fundamental laser field combined with a THz field are also calculated in Fig.  2. From Fig.  2 we can see that the ionization probability in both cases presents the same tendency: the curve increases rapidly at first, then almost keeps the same. While after adding the THz field, ionization occurs earlier, and ionization probability is also higher in combined laser field case, especially at T = − 0.67  o.c.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. Ionization probability in a 800-nm fundamental laser field only and a 800-nm fundamental laser field combined with a THz field, respectively.

Figure  3 shows the time– frequency distribution of the HHG ((a1), (a2)) and corresponding three-step models ((b1), (b2)) in a 800-nm fundamental laser field only and a 800-nm fundamental laser field combined with a THz field, respectively. In Fig.  3(a1), there are four main peaks contributing to the HHG, which are marked as P₁, P₂, P₃, and P₄. For harmonic orders above 35^th, the peak of P₄ almost makes no contribution to the HHG. Thus, only peaks P₁, P₂, and P₃ are left for the HHG. The maximum harmonic orders of P₁, P₂, and P₃ are about 62^th, 53^th, and 50^th, respectively. The three peaks with both long and short trajectories (a trajectory with earlier ionization time but later emission time is called the long trajectory, and a trajectory with later ionization time but earlier emission time is called the short trajectory) all contribute to the HHG, and the intensity of long and short trajectories is comparable, leading to modulations in the harmonic spectrum, which is disadvantageous to synthesis single attosecond pulse. From Fig.  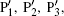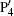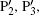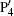3(a2) we can see that there are also four peaks marked as and in the combined laser pulse case, the three peaks and are suppressed, and only the peak is left to contribute to the HHG for the harmonics from 60^th to 95^th order. For peak , two dominant quantum paths (short trajectory and long trajectory) with different emission times contribute to the same harmonic in half optical cycle of the fundamental pulse. It is apparently seen that the long trajectory is suppressed and the short one is relatively enhanced. Then for the harmonics in the plateau, the time of two paths are different and the harmonics are not in phase. Apparently, the contribution of short trajectory is higher than the long one, thus a single quantum path control is realized, which is advantageous to produce an isolated attosecond pulse.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Time– frequency distribution of the HHG ((a1), (a2)) and corresponding three-step models ((b1), (b2)) in a 800-nm fundamental laser field only and a 800-nm fundamental laser field combined with a THz field, respectively.

Figure  3(b1) is the three-step model corresponding to a 800-nm fundamental laser field only case, and there are four major peaks of emission time marked as A, B, C, and D. The peaks A, B, and C all contribute to HHG. The maximum harmonic frequency of 60ω ₁ is consistent with the cutoff position shown in Fig.  1(b) with the black dotted curve. In Fig.  3(b2), after adding a THz field in the 800-nm fundamental laser field, only the peak A′ is left to contribute to HHG for the harmonics over order of 60^th, with the maximum harmonic frequency equal to 95ω ₁. Thus, the cutoff of harmonics can be extended, which is consistent with the result shown by the red solid curve in Fig.  1(b). For peak A′ , electrons with the short trajectory are mainly ionized from T = − 0.67  o.c. to T = − 0.48  o.c., and electrons with the long trajectory are mainly ionized from T = − 0.80  o.c. to T = − 0.67  o.c. However, the ionization rate of electrons corresponding to the short trajectory is much higher than that corresponding to the long trajectory (see the red solid curve in Fig.  2). Consequently, the harmonic intensities for the short trajectory are much higher than that for the long trajectory, which is consistent with the time– frequency distribution (see Fig.  3(a2)).

Figure  4 shows the case of a 800-nm fundamental laser field, by superposing the HHG from the 40^th to the 60^th order, and a 252-as pulse and a relative weak 201-as pulse can be achieved. For the case of the combination of a 800-nm fundamental laser field combined with a THz field, the HHG spectrum of plateau is smoother and with much fewer modulation. Thus, by superposing the harmonics in the range from 75^th to 95^th order, an isolated attosecond pulse with duration of about 133 as can be obtained.

Fig.  4.

Figure Option ViewDownloadNew Window

Fig.  4. Temporal profiles of the attosecond pulses generated from H atom: the black dotted curve describes the temporal profiles by superposing the harmonics from 40th to 60th order in a 800-nm fundamental laser field (5  fs); the red solid curve describes the temporal profiles by superposing the harmonics from 75th to 95th order in a 800-nm fundamental laser field combined with a THz field (5  fs/800 nm, 16  fs/4800 nm).

In conclusion, we theoretically investigate the high-order harmonic generation of H atom in a 800-nm fundamental laser field combined with a THz field by solving the time-dependent Schrö dinger equation accurately with TDGPS method. The result shows that the plateau of high-order harmonic is extended in the presence of THz field, which can be explained by the corresponding ionization probability. With the combined laser field, the long trajectory can be suppressed and the short trajectory can be enhanced. As a result, the optimizing combined field allows electrons to acquire more kinetic energy from the laser field, leading to the extension of the HHG plateau, and an isolated 133-as pulse can be generated.