The interaction between an atom and an intense laser pulse can cause lots of fundamental strong-field physics phenomena, such as above-threshold ionization (ATI), high-harmonic generation (HHG), and nonsequential double ionization (NSDI). In the above-threshold ionization, atoms or molecules absorb more photons than necessary for ionization, which was firstly discovered by Agostini et al.^[1] Since the discovery of ATI, the ionization of an atom in two-color laser pulses has attracted much attention for understanding the stimulated absorption and emission of photons in the ATI process.^{[2– 7]} Muller et al. observed a sideband structure in the ATI spectrum, which may be due to the stimulated absorption and emission of low-frequency photons.^[2] Koval et al. investigated the ATI process of an atom in a two-color laser field of the first and the third harmonics. They found that the cutoff of the ATI spectrum depends on the relative phase between the two color laser fields.^[7] Furthermore, Paulus et al. also found that the cutoff of the photoelectron spectrum strongly depends on the relative phase of the two color laser fields with the frequencies being the fundamental and the second harmonics.^[5]

Recently, with the development of high-frequency attosecond pulse techniques via HHG and free-electron lasers, ionization of atoms in IR+ XUV two-color laser fields has become a hot topic.^{[8– 18]} Kazansky et al. investigated the angle-resolved spectra of photoelectrons produced by IR+ XUV two-color laser pulses. Radcliffe et al. observed a plateau-shape envelope of the ATI spectrum with increasing intensity of the IR laser field. Moreover, Zhang et al. found a step-like structure of the ATI spectrum in IR+ XUV two-color laser fields. In this paper, we investigate the dependence of the ATI spectrum on the polarization directions of the two-color laser fields. We find that, when the photon energies of both lasers are much smaller than the atomic ionization threshold, the ionization channel interference is very obvious, and hence the ionization spectrum strongly depends on the angle between the two lasers’ polarization directions. While when one laser’ s photon energy approaches or is larger than the atomic ionization threshold, the channel interference disappears, hence the ATI spectrum is independent of the angle between the two lasers’ polarization directions, and several dips appear in the spectrum at certain angles.

The frequency-domain theory for the ATI process of an atom in a two-color laser field has been presented in detail.^{[18– 20]} Here we briefly summarize the basic idea of this theory for completeness and modify the theory for the case in which the two linear polarized lasers have different polarization directions. Atomic units are used throughout the paper, unless specified otherwise. We consider the ionization of an atom in a two-color laser field. The Hamiltonian of this atom– laser system is H = H₀ + U(r) + V, where

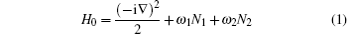
is the free-electron and free-photon Hamiltonian, N_i is the photon number operator of the field with frequency ω _i, i = 1, 2, U(r) is the atomic binding potential, and V describes the electron– photon interaction. Based on the formal scattering theory of multiphoton ionization in strong fields, ^[21] the transition matrix from the initial quantum state ψ _i to the final state ψ _f can be expressed as

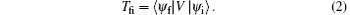
The initial quantum state ψ _i can be expressed as

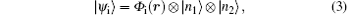
with the initial energy being E_i = – I_p + (n₁ + 1/2)ω ₁ + (n₂ + 1/2)ω ₂. Here, Φ _i(r) is the ground state of the atom, | n_j〉 is the Fock state with photon number n_j (j = 1, 2), and I_p is the ionization threshold of the atom. The final state ψ _f, which is the quantized-field Volkov state, can be represented as^{[19, 20]}

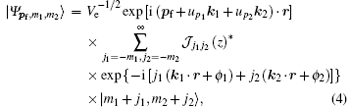
where V_e is the normalization volume, p_f is the momentum of the ionized electron, u_pj is the ponderomotive energy in units of frequency ω _j, and k_j is the photon momentum of the two laser fields with j = 1, 2. The ϕ _j is the initial phase of the two laser fields, which is set to be zero for simplicity in this paper. The total energy of the final state is

where m₁ and m₂ are the photon numbers in the two laser fields.

In Eq.  (4), the generalized Bessel function can be written as

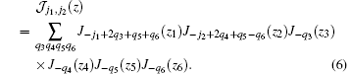
Here, z ≡ (z₁, z₂, z₃, z₄, z₅, z₆), and we have

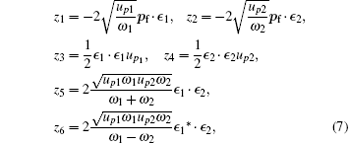
where ∊ ₁ and ∊ ₂ are the polarization directions of the two laser fields. By using the initial and the final states, equation  (2) can be expressed as

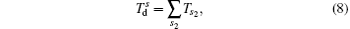
with

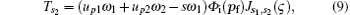
where sω ₁ = s₁ω ₁ + s₂ω ₂ is the total photon energy that the electron absorbs from both laser fields, and s₁ = n₁ − m₁ and s₂ = n₂ − m₂ are the absorbed photon numbers from the two laser fields. We now define θ ₁ (θ ₂) as the angle between the polarized direction of the first (second) laser field and the emission direction of the ionized electron, θ ₃ as the angle between the polarized directions of the two laser fields, then the generalized Bessel function in Eq.  (6) can be rewritten as

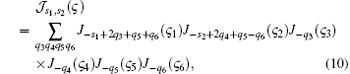
where

with c being the speed of light. In this paper, the emission direction of the ionized electron is set along the first laser’ s polarization direction, hence we have θ ₁ = 0, and assume θ ₂ = θ ₃ = θ .

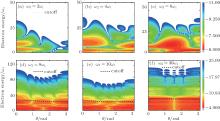
Figure  1 presents the photoelectron spectra as a function of the angle θ between the polarization directions of the two lasers with ω ₂ = 2ω ₁, 4ω ₁, 6ω ₁, 8ω ₁, 10ω ₁, and 30ω ₁. The frequency of the first laser is ω ₁ = 1.165  eV. The laser intensity I₁ = I₂ = 3.6 × 10¹³  W/cm², corresponding to the ponderomotive value of the first laser U_p1 = 3.2ω ₁, and that of the second laser U_p2 = 0.8ω ₁, 0.20ω ₁, 0.089ω ₁, 0.05ω ₁, 0.032ω ₁, and 0.0036ω ₁ for ω ₂ = 2ω ₁, 4ω ₁, 6ω ₁, 8ω ₁, 10ω ₁, and 30ω ₁, respectively. The ionization threshold of the hydrogen-like atom is I_p = 12.1 eV. One can find that the spectrum strongly depends on the angle θ for the case of ω ₂ = 2ω ₁, as shown in Fig.  1(a), where the cutoffs for θ = 0 and 180° are about 26ω ₁ and 10ω ₁, respectively. As shown in Figs.  1(b)– 1(f), when ω ₂ increases, the dependence of the spectrum on the angle decreases rapidly, and the spectrum with ω ₂ = 30ω ₁ shows a symmetrical structure.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Electron spectra as a function of the angle between the two lasers’ polarization directions in two-color laser fields with ω 1 = 1.165  eV, and ω 2 = 2ω 1 (a), 4ω 1 (b), 6ω 1 (c), 8ω 1 (d), 10ω 1 (e), 30ω 1 (f). The laser intensity I1 = I2 = 3.6 × 1013  W/cm2.

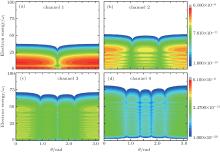
To understand the spectral characteristics shown in Fig.  1, we define the quantum channel by the photon number s₂ that the atom absorbs from the high-frequency laser. Therefore, the transition matrix of the s₂ channel is expressed by Eq.  (9). Figures  2 and 3 present the ATI spectra as a function of angle θ for different channels with ω ₂ = 2ω ₁ and 10ω ₁, respectively. We find that all spectra are symmetrical about θ = π /2. However, the cutoff of the spectrum for the case of ω ₂ = 2ω ₁ decreases as the angle increases from 0 to π /2, as shown in Fig.  2; while that for the case of ω ₂ = 10ω ₁ keeps unchanged as the angle increases and the spectrum only shows several dips at certain angles for different channels.

Fig.  2.

	Figure Option ViewDownloadNew Window
	Fig.  2. ATI spectra as a function of the angle between the two lasers’ polarization directions for channel 1 (a), 2 (b), 3 (c), and 4 (d) with ω 1 = 1.165  eV, ω 2 = 2ω 1. The laser intensity I1 = I2 = 3.6 × 1013  W/cm2.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. ATI spectra as a function of the angle between the two lasers’ polarization directions for channel 1 (a), 2 (b), 3 (c), and 4 (d) with ω 1 = 1.165  eV and ω 2 = 10ω 1. The laser intensity I1 = I2 = 3.6 × 1013  W/cm2.

By analyzing the property of the Bessel function in Eq.  (9), the symmetry characteristics of the spectra for all channels shown in Figs.  2 and 3 can be explained as follows. By using the integral formula of the Bessel function

we can express the Bessel function by its Taylor’ s series expansion as

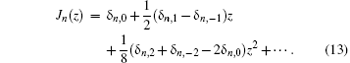
By inserting the Taylor expansions of Bessel functions J_{− s2+ 2q4+ q5− q6}(ς ₂), J_{− q5}(ς ₅), and J_{− q6}(ς ₆) into Eq.  (9), for the odd channels with s₂ = 2n + 1, n = 0, 1, … , the Bessel function can be rewritten as

while for the even channels with s₂ = 2n, n = 0, 1, … , it can be expressed as

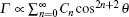
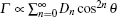
Since the ionization rate Γ of each channel is proportional to | 𝓣 _{s1, s2}(ς )| ², we therefore find that for the odd channels, and for the even channels, where C_n and D_n are nonzero parameters which can be obtained by using Eq.  (10). As a result, the spectra of all channels are symmetrical about θ = π /2.

Comparing the spectra of Figs.  1(a) and 1(f), we find that, for the case of ω ₂ = 2ω ₁, the cutoff of the total ATI spectrum decreases as θ increases from 0 to π , and the spectral symmetry for separate channels shown in Fig.  2 completely disappears; while for the case of ω ₂ = 30ω ₁, the ATI spectrum shows a multi-plateau structure with the cutoff of each plateau being independent of the angle θ , and the symmetry of the channel spectra about θ = π /2 remains. To understand these differences, we present the ATI spectra for the first five channels with θ = 0, 180° and ω ₂ = 2ω ₁, 4ω ₁, 6ω ₁, 10ω ₁ in Fig.  4. We find that the five channels have comparable contributions to the total ATI spectrum when ω ₂ = 2ω ₁, as shown in Figs.  4(a) and 4(e). While only the first three channels dominate the contributions to the spectrum when ω ₂ = 4ω ₁, as shown in Figs.  4(b) and 4(f). Finally, the contributions to the spectrum from different channels completely separate and the ATI spectrum has a step-like structure when ω ₂ ≥ 10ω ₁, as shown in Figs.  4(d) and 4(h). The quantum interference of the channels induces the dramatic dependence of the ATI spectrum on the angle θ for the case of ω ₂ = 2ω ₁; while the interference between the channels disappears for ω ₂ ≥ 10ω ₁, and hence the total spectrum is independent of the angle.

Fig.  4.

	Figure Option ViewDownloadNew Window
	Fig.  4. Electron spectra for different channels with the angle between the two lasers’ polarization directions θ = 0 ((a)– (d)) and 180° ((e)– (h)). Here ω 1 = 1.165  eV, and ω 2 = 2ω 1 ((a) and (e)), 4ω 1 ((b) and (f)), 6ω 1 ((c) and (g)), 10ω 1 ((d) and (h)).

When ω ₂ = 2ω ₁, we may regard both lasers as classical fields, hence we can obtain the cutoff of the total ATI spectrum by using the saddle-point approximation to the Bessel function in Eq.  (8).^{[22– 25]} In general, the classical action function of an electron moving in a two-color laser field A_c(t) = ∊ ₁A₁ cos(ω ₁t) + ∊ ₂A₂ cos(ω ₂t) can be written as

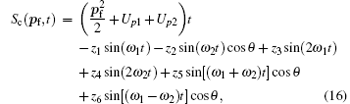
where p_f is set along the direction of ∊ ₁, and the angle between ∊ ₁ and ∊ ₂ is θ , which corresponds to the quantum numerical calculation condition. On the other hand, by using the integral form of the Bessel function, the generalized Bessel function Eq.  (11) can be written as

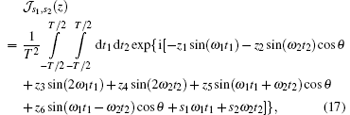
hence we have

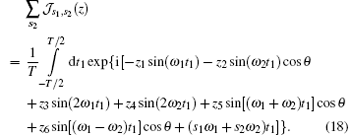
Therefore, we obtain the relationship between the Bessel function and the classical action function

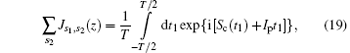
where 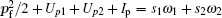. By using the saddle-point approximation, we obtain the energy equation from Eq.  (19)

which has the same form as that in the monochromatic low-frequency laser case.^[26] By setting I_p to 0, we obtain the cutoff of the ATI spectrum with Eq.  (20), which is shown by the solid curve in Fig.  1(a). We find that the cutoff curve agrees well with the quantum numerical results. These results indicate that the ATI spectrum depends on the angle between the two laser polarization directions when both laser fields can be treated as classical fields.

However, when ω ₂ ≥ 10ω ₁, the high-frequency laser field must be regarded as a quantum field, rather than a classical one. Therefore, the cutoff equation (20) is no longer suitable for the high-frequency laser case. Under our present calculation conditions, we find that the spectra for different channels completely separate from each other, as shown in Fiqs.  1(d)– 1(f), hence the ATI transition matrix element now becomes 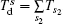. 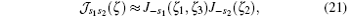Furthermore, the arguments of ς ₄, ς ₅, and ς ₆ in the Bessel function of Eq.  (10) are much smaller than 1 due to the small value of U_p2 for ω ₂ ≥ 10ω ₁. Therefore, the Bessel function J_qi(ς _i) ≈ 0 for i = 4, 5, 6 in Eq.  (10), and hence the Bessel function of Eq.  (10) can be simplified as^[18]

where s₁ and s₂ are the numbers of photons of frequencies ω ₁ and ω ₂ that the electron absorbs, and . As a result, the matrix element of channel s₂ can be written as

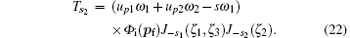
Although the high-frequency ω ₂ laser field cannot be treated as a classical field, the low-frequency ω ₁ laser field can still be regarded as a classical field. Therefore, the cutoff of the ATI spectrum for each s₂ channel can be obtained by using the saddle-point approximation for the Bessel function J_{– s1}(ζ ₁, ζ ₃) in Eq.  (22) with a certain value of s₂. Similarly, we now have the energy relationship

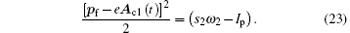
The dashed lines in Figs.  1(d)– 1(f) show the cutoff with s₂ = 1 obtained by Eq.  (23) with I_p keeping its value. We find that the cutoff curves agree well with the numerical calculation. Moreover, since the cutoff formula is independent of the high-frequency ω ₂ laser field, the cutoff keeps unchanged with increasing θ .

Based on the frequency-domain theory, we investigate the dependence of the ionization of an atom on the angle between the polarization directions of the two laser fields. We find that the angle dependence of the ATI spectrum is related to the frequencies of the two laser fields. When the photon energies of the two lasers are much smaller than the atomic ionization threshold, both laser fields can be regarded as classical fields, hence the channel interferences are very strong, and the ATI spectrum depends on the angle between the two lasers’ polarization directions. While when one laser’ s photon energy is larger than the atomic ionization threshold, this high-frequency laser field can only be treated as a quantum field, and the channel interference disappears, resulting in that the ATI spectrum is independent of the angle between the lasers’ polarization directions, and only several dips appear at certain angles.