Cite this Article
Wu Yan-Qiu†. Output power analyses of an endoreversible Carnot heat engine with irreversible heat transfer processes based on generalized heat transfer law . Chinese Physics B, 24(7): 070506  
Permissions
Output power analyses of an endoreversible Carnot heat engine with irreversible heat transfer processes based on generalized heat transfer law
Wu Yan-Qiu†
Chongqing Three Gorges University, Chongqing 404100, China

†Corresponding author. E-mail: wuyanqiu0516@126.com

*Project supported by the Youth Programs of Chongqing Three Gorges University, China (Grant No. 13QN18).

Abstract

In this paper, an endoreversible Carnot heat engine with irreversible heat transfer processes is analyzed based on generalized heat transfer law. The applicability of the entropy generation minimization, exergy analyses method, and entransy theory to the analyses is discussed. Three numerical cases are presented. It is shown that the results obtained from the entransy theory are different from those from the entropy generation minimization, which is equivalent to the exergy analyses method. For the first case in which the application preconditions of the entropy generation minimization and entransy loss maximization are satisfied, both smaller entropy generation rate and larger entransy loss rate lead to larger output power. For the second and third cases in which the preconditions are not satisfied, the entropy generation minimization does not lead to the maximum output power, while larger entransy loss rate still leads to larger output power in the third case. For the discussed cases, the concept of entransy dissipation is not applicable for the analyses of output power. The problems in the negative comments on the entransy theory are pointed out and discussed. The related researchers are advised to focus on some new specific application cases to show if the entransy theory is the same as some other theories.

PACS: 05.70.Ln; 44.90.+c
Keyword: entropy generation; exergy destruction; entransy; endoreversible Carnot heat engine
1. Introduction

The endoreversible Carnot heat engine with irreversible processes is very important in engineering and attracts more and more attention.[1– 5] The entropy generation minimization, exergy analyses method, and some other theories have been applied to the analyses of this kind of heat engines.[2, 3] For instance, the entropy generation minimization is used to maximize the output work of thermodynamic cycles.[3] In recent years, the entransy theory, which was proposed by the analogy between heat and electrical conductions[6] and applied to many heat transfer problems, [6– 21] has also been extended to the analyses of thermodynamic systems[22– 33] and applied to some Carnot heat engines with irreversible processes.[2, 3, 23] For instance, Aç ι kkalp[2] used the concept of entransy to analyze the irreversible Carnot-like heat engine. Cheng and Liang[23] applied the concept of entransy loss to designing the operation parameters of the Carnot heat engines in the discussed one-stream heat exchanger networks.

For the concepts of entropy generation and exergy, the Gouy– Stodola theorem shows that the exergy destruction equals the product of the entropy generation and environment temperature.[34] Therefore, the entropy generation minimization and exergy analyses method are equivalent when the environment temperature is fixed. These two methods are often used in the analyses of thermodynamic systems[2, 3] because the concept of entropy generation can measure the irreversibility of thermodynamic processes and the decrease of irreversibility can improve the thermodynamic performance for the discussed systems. However, when the concept of entropy generation is applied to the Carnot heat engines in the one-stream heat exchanger networks, it is found that the entropy generation minimization does not always lead to the maximum output power.[23] Therefore, there are different viewpoints on the applicability of entropy generation minimization and exergy analyses method to the analyses of thermodynamic processes.

For the entransy theory, there are not many papers on its application to the Carnot heat engine with irreversible processes. Furthermore, as a theory which is under developing, there are some doubts and negative comments.[35– 45] For instance, Bejan[35, 36] thought that the entransy theory is a copy of the constructal theory. Grazzini et al.[38] thought that entransy dissipation analysis is a duplicate of entropy generation analysis. These doubts and negative comments have all been replied and discussed, and it has been shown that the entransy theory has its physical basis and advantages in applications.[46– 52] However, the applicability of entransy theory to the Carnot heat engine with irreversible processes still needs further investigations.

In this paper, the concepts of entropy generation, exergy, entransy loss and entransy dissipation are applied to an endoreversible Carnot heat engine with irreversible heat transfer processes, and the applicability of the concepts is also discussed.

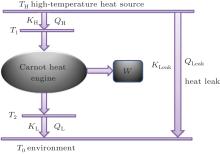
2. Analyses of an endoreversible Carnot heat engine with irreversible heat transfer processes
2.1. System description and expressions of the discussed parameters

The endoreversible Carnot heat engine with irreversible heat transfer processes can be shown in Fig.  1. In the system, the heat flow rate, QH, from the high-temperature heat source at temperature TH gets into the Carnot heat engine which works between the temperatures T1 and T2. The output power of the system is W, and the rest heat flow rate, QL, finally releases to the environment at temperature T0. For the system, we should consider the heat leak rate, QLeak, between the high-temperature heat source and environment.

Fig.  1. An endoreversible Carnot heat engine with irreversible heat transfer.

Assuming that the heat transfer processes satisfy the generalized heat transfer law, [53– 55] we have

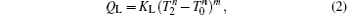
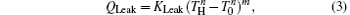
where KH is the product of the heat transfer area and corresponding heat transfer coefficient between the high-temperature heat source and working fluid of the Carnot cycle, KL is the product of the heat transfer area and corresponding heat transfer coefficient between the working fluid of the Carnot cycle and environment, KLeak is the product of the heat transfer area and corresponding heat transfer coefficient between the high-temperature heat source and environment, and m and n are constants. With different heat transfer laws, m and n have different values. For instance, the heat transfer law is the Newton heat transfer law if m = n = 1, while it is the radiative heat transfer law if m = 1 and n = 4.

According to the Carnot theorem, we can obtain

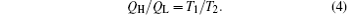
The energy conservation indicates that the output power is

The entropy generation rate of the system, Sg, is

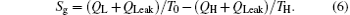
According to the Gouy– Stodola theorem, the exergy destruction rate can be expressed as

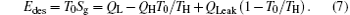
Considering that the environment temperature is fixed, equation  (7) shows that the variation tendency of the exergy destruction rate is the same as that of the entropy generation rate.

On the other hand, the entransy theory can also been applied. Considering the definition of entransy loss rate Gloss, [22] we have

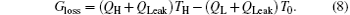
The entransy dissipation rate Gdis is[56]

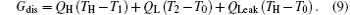
2.2. Numerical examples and discussion

To analyze the relationships of the output power W, entropy generation rate Sg, exergy destruction rate Edes, entransy loss rate Gloss, and entransy dissipation rate Gdis, we can discuss three numerical cases below. In the following, we will not calculate the exergy destruction rate because the variation of the exergy destruction rate is the same as that of the entropy generation rate.

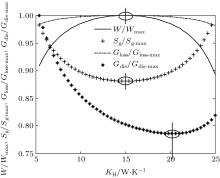
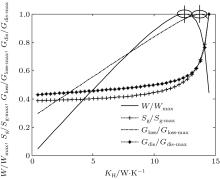
In the first case, we assume that TH = 800  K, T0 = 300  K, QH = 800  W, KLeak = 1  W/K, KH + KL = 30  W/K, and m = n = 1. The Newton heat transfer law is used here. Based on Eqs.  (1)– (9), the variations of the output power W, entropy generation rate Sg, entransy loss rate Gloss and entransy dissipation rate Gdis with KH can be obtained. The results are shown in Fig.  2. It can be found that the output power W reaches its maximum value when KH = 14.8  W/K. At the same time, the entropy generation rate Sg arrives at its minimum value and the entransy loss rate Gloss reaches its maximum value, respectively. However, the entransy dissipation rate Gdis neither reaches its maximum value nor its minimum value.

Fig.  2. Variations of W, Sg, Gloss, and Gdis with KH when QH is fixed and m = n = 1.

If we use the concept of entransy loss to analyze thermodynamic systems, Cheng and Liang[54] showed that larger entransy loss rate leads to larger output power when the equivalent temperatures of the high- and low-temperature heat source and the heat flow rate from the high-temperature heat source are given. In the first case, as TH, T0, and KLeak are fixed, equation  (3) shows that QLeak is fixed. Therefore, TH (temperature of the high-temperature heat source), T0 (temperature of the low-temperature heat source) and the sum of QH and QLeak (heat flow rate from the high-temperature heat source) are all fixed. Then, the preconditions[57] with which the concept of entransy loss can be used to optimize the output power of the thermodynamic cycle are all satisfied. This is the reason why the maximum entransy loss rate corresponds to the maximum output power in this case. With Eqs. (5) and (8), we have

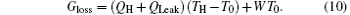
It is very clear that larger entransy loss rate leads to larger output power with prescribed TH, T0, and sum of QH and QLeak.

On the other hand, if the concept of entropy generation is used, it is found that the entropy generation minimization leads to the maximum output power when the net exergy flow rate from the high-temperature heat source, Enet, and environment temperature are given.[32, 58] It is shown that[32, 58]

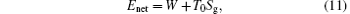
so the entropy generation minimization leads to the maximum output power when Enet and T0 are given. In the first case, Enet can be expressed by

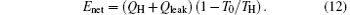
It can be seen that Enet is also fixed. Then, the preconditions[32, 51] with which the entropy generation minimization can be used to optimize thermodynamic cycles are also satisfied. This is the reason why the entropy generation minimization corresponds to the maximum output power in this case.

As the exergy destruction rate has the same variation tendency as that of the entropy generation rate, the minimum exergy destruction rate would also lead to the maximum output power. For the entransy dissipation rate, its extremum values do not correspond to the maximum output power, which shows that this concept is not applicable for the optimization of the output power in this case. This is because this concept was not developed for thermodynamic cycles, but for heat transfer processes.[6, 7] Cheng et al.[59] noted this point when they analyzed the endoreversible Carnot cycle. They also found that the concept of entransy dissipation is not suitable for the analyses of the discussed thermodynamic cycles.

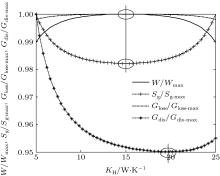
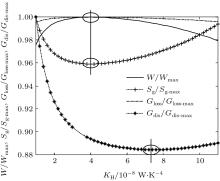
In this case, if we change the values of m and n, some other heat transfer laws can be calculated. When m = 0.5 and n = 2, the other parameters are assumed to the same as those in the calculation above. Then, the variations of the output power W, entropy generation rate Sg, entransy loss rate Gloss, and entransy dissipation rate Gdis with KH can also be obtained and shown in Fig.  3. When m = 1 and n = 4, we assume that Kleak = 1 × 10− 9  W/K4, KH + KL = 2 × 10− 8  W/K4, and the other parameters are the same as those in the calculation above. The results can be shown in Fig.  4. It can be seen that different heat transfer laws do not affect the variation tendencies of the calculated parameters. The entransy loss rate and output power also get their maximum values at the same time, while the entropy generation rate gets its minimum value. The extremum values of entransy dissipation rate do not correspond to the maximum output power, either. Therefore, the discussion on the applicability of the entropy generation minimization and entransy theory above is also tenable for other discussed heat transfer laws.

Fig.  3. Variations of W, Sg, Gloss, and Gdis with KH when QH is fixed, m = 0.5, and n = 2.

Fig.  4. Variations of W, Sg, Gloss, and Gdis with KH when QH is fixed, m = 1, and n = 4.

In the second case, we assume that TH = 800  K, T0= 300  K, T1 = 760  K, KLeak = 0.5  W/K, and KH + KL = 16  W/K. With Eqs.  (1)– (6), the variations of the output power W, entropy generation rate Sg, entransy loss rate Gloss, and entransy dissipation rate Gdis with KH can also be obtained. The results are shown in Fig.  5, in which we can find that the output power W reaches its maximum value when KH = 15.6  W/K. At this point, none of the entropy generation rate Sg, entransy loss rate Gloss, and entransy dissipation rate Gdis reaches an extremum value. Considering that the variation tendencies of the exergy destruction rate and entropy generation rate are the same, we can conclude that none of the entropy generation minimization, exergy analyses method, and entransy theory is applicable for the optimization of the output power in this case. Here, QH is not fixed, so neither the heat flow rate nor the net exergy flow rate from the high temperature heat source is given. The preconditions for the application of the theories are not satisfied. This is the reason why none of the theories is applicable.

Fig.  5. Variations of W, Sg, Gloss, and Gdis with KH when T1 is fixed and m = n = 1.

In this case, some other heat transfer laws are also used. When m = 0.5, n = 2, we assume that the other parameters are the same as those in the calculation above. When m = 1 and n = 4, we assume that KLeak = 1 × 10− 8  W/K4, KH + KL = 1 × 10− 7  W/K4, and the other parameters are the same as those in the calculation above. The results are presented in Figs.  6 and 7, respectively. From the numerical results, it can also be found that neither the entropy generation minimization nor the entransy theory is applicable for the optimization of output power under these heat transfer laws.

Fig.  6. Variations of W, Sg, Gloss, and Gdis with KH when T1 is fixed, m = 0.5, and n = 2.

Fig.  7. Variations of W, Sg, Gloss, and Gdis with KH when T1 is fixed, m = 1, and n = 4.

In the third case, we assume that TH = 800  K, T0 = 300  K, T1 = 750  K, T2 = 400  K, and QLeak = 200 W. Considering Eqs.  (1)– (9), we can obtain the variations of the output power W, entropy generation rate Sg, entransy loss rate Gloss, and entransy dissipation rate Gdis with KH. The results are shown in Fig.  8, in which it can be found that all the output power W, entropy generation rate Sg, entransy loss rate Gloss, and entransy dissipation rate Gdis increase monotonously with the increase of KH. Here, different heat transfer laws are also calculated. We find that different heat transfer laws do not affect the variation tendencies of the discussed parameters. The curves under different heat transfer laws are similar to those in Fig.  8, so they are not presented here.

Fig.  8. Variations of W, Sg, Gloss, and Gdis with KH when T1 and T2 are fixed and m = n = 1.

In this case, QH is not fixed either. However, the numerical results show that larger values of entransy loss rate and entransy dissipation rate lead to larger output power, while smaller entropy generation rate does not. As the variation of the exergy destruction rate is the same as that of the entropy generation rate, we can conclude that the entropy generation minimization and exergy analyses method are not applicable for the optimization of output power in this case, while the concept of entransy loss is.

3. Discussion on the comments on the entransy theory

As above, the concepts of entropy generation, exergy, entransy loss and entransy dissipation are applied to the analyses of the Carnot cycle with irreversible heat transfer processes. Three cases are analyzed numerically. In our cases, it is shown that the variation tendencies of the entropy generation rate and exergy destruction rate are the same, while the numerical results of the entransy theory and entropy generation minimization are different. Our conclusion is different from some negative comments on the entransy theory, [36– 38, 42, 43, 60] in which the authors told us that the entransy theory gives the same analyses results as those of the entropy generation minimization. These comment papers are discussed below.

In Refs.  [36]– [38], [42], and [43], the entransy theory is mainly commented by theoretical analyses in which Xu’ s work[61] is important basis. However, it is found that Xu’ s derivation is not correct, [62] so the conclusions based on Xu’ s work may need further inspection. The questions and doubts in Refs.  [35]– [45] were also replied and explained in Refs.  [46]– [51].

Moreover, the negative comments papers[35– 45] show that the authors mainly cited the viewpoints of their side, neglecting the viewpoints and replies from the other side. For instance, Grazzini and Rocchetti[39] only showed their viewpoints on entransy in the Introduction section of their paper, without any further analysis or discussion. They cited some negative comment papers on entransy but no reply papers. In the review paper, [43] Manjunath and Kaushik also discussed the entransy theory based on the viewpoints of the negative comment papers, neglecting the viewpoints on the other side. This is unfair and unscientific.

Especially, Grazzini[38, 39] and Awad[41, 42] both commented the entransy theory twice, respectively. Bejan[35, 36, 44, 45] even commented the entransy theory four times. However, none of them mentioned the replies[44, 47] of their first comment papers[35, 38, 41] in their subsequent comment papers.[36, 39, 42, 44, 45] They only repeated their viewpoints. Awad[41] wrote that “ Repetition does not mean refutation” at the end of his first comment paper. However, when commenting the entransy theory for the second time, Awad himself[42] repeated his questions, such as “ Guo et al. replace ‘ analogy’ with ‘ simplified expression” ’ , [41, 42] “ entransy does not have the units of energy” , [41, 42] etc., which have already been replied and discussed.[48, 49] Therefore, once again, his questions and doubts were replied.[50]

In our opinion, if the researchers on both sides can focus on some new specific application cases, it may be helpful to make the discussion and argument clear. For instance, in the present paper, our examples show that the entransy theory is different from the entropy generation minimization. However, Oliveira and Milanez[60] also gave some application cases that show us “ the results obtained by the entransy concept are identical to those obtained by the entropy generation minimization technique” . Here, we should point out that there are mainly two problems in Ref.  [60]. First, at the end of Section  2, the authors wrote that “ Eq.  (12) (the expression of entransy dissipation rate) is the main expression of this article, being used to show that the application of the concept of entransy is equivalent to applying the concept of the minimum entropy generation rate.” Our numerical results and the work of Cheng et al.[59] showed that the concept of entransy dissipation is not applicable to the analyses of the discussed thermodynamic processes, so maybe Oliveira and Milanez[60] chose the wrong concept in entransy theory to analyze their cases. Second, the expression of entransy dissipation rate in Ref.  [60] is

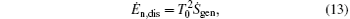
where Ṡ gen expresses the entropy generation rate in Ref.  [60]. We can take a simple example to show that equation  (13) is not correct. Let us consider a simple one-dimensional heat transfer process, in which the heat flow rate Q is transferred from the high temperature heat source at temperature TH to the environment at temperature T0. Considering the definition of entransy dissipation rate, [6] we have

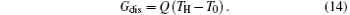
The entropy generation rate of this process is

It is very easy to find that

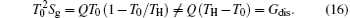
Therefore, the main conclusion of Ref.  [60] is not correct. If the suitable concept and right expression are applied, different conclusions can be obtained.

For the other doubts on entransy theory, our advice can also be considered. For instance, Bejan[35, 36] claimed that the entransy theory is a copy of the constructal theory. For this problem, if the related researchers on both sides can focus on some new specific application cases in which both the entransy theory and constructal theory can be applied, the optimization results will show us if the two theories are the same.

4. Conclusions

Based on generalized heat transfer law, we analyze an endoreversible Carnot heat engine with irreversible heat transfer processes by the entropy generation minimization, exergy analyses method, and entransy theory in this paper. Three different numerical examples are calculated. Some conclusions can be obtained as follows.

i) For the three cases, the results obtained from the entropy generation minimization and those from the exergy analyses method are equivalent because the variation tendencies of entropy generation rate and exergy destruction rate are the same.

ii) The results obtained from the entransy theory are different from those from the entropy generation minimization. For the first case in which the application preconditions of the entropy generation minimization and entransy loss maximization are satisfied, both smaller entropy generation rate and larger entransy loss rate lead to larger output power. For the second and third cases in which the preconditions are not satisfied, the entropy generation minimization does not lead to the maximum output power, while larger entransy loss rate still leads to larger output power for the third case. For the discussed three cases, the concept of entransy dissipation is not applicable for the analyses of output power.

iii) The negative comments on the entransy theory are discussed. The main problems in the comments papers are pointed out, and Oliveira and Milanez’ s conclusion that “ the results obtained by the entransy concept are identical to those obtained by the entropy generation minimization technique” [60] is not correct. We have shown that the entransy theory is different from the entropy generation minimization with specific application cases. The related researchers on both sides are advised to focus on some new specific application cases to show if the entransy theory is the same as some other theories.

Reference
1 Salas N S, Velasco S and Hernández A C 2002 Energy Convers. Manage. 43 2341 DOI:10.1016/S0196-8904(01)00169-8 [Cited within:1]
2 Açιkkalp E 2014 Energy Convers. Manage. 80 535 DOI:10.1016/j.enconman.2014.01.056 [Cited within:4]
3 Cheng X T and Liang X G 2013 Chin. Phys. B 22 010508 DOI:10.1088/1674-1056/22/1/010508 [Cited within:4]
4 Nie W, He J and Deng X 2008 Int. J. Thermal Sci. 47 633 DOI:10.1016/j.ijthermalsci.2007.04.004 [Cited within:1]
5 Liu X W, Chen L G, Wu F and Sun F R 2014 J. Energy Institute 87 69 DOI:10.1016/j.joei.2014.02.008 [Cited within:1]
6 Guo Z Y, Zhu H Y and Liang X G 2007 Int. J. Heat Mass Transfer 50 2545 DOI:10.1016/j.ijheatmasstransfer.2006.11.034 [Cited within:4]
7 Chen L G 2012 Chin. Sci. Bull. 57 4404 DOI:10.1007/s11434-012-5477-4 [Cited within:1]
8 Chen L G, Xiao Q H, Xie Z H and Sun F R 2013 Int. J. Heat Mass Transfer 67 506 DOI:10.1016/j.ijheatmasstransfer.2013.08.073 [Cited within:1]
9 Chen L G, Xiao Q H, Xie Z H and Sun F R 2012 Int. Comm. Heat Mass Transfer 39 1556 DOI:10.1016/j.icheatmasstransfer.2012.09.003 [Cited within:1]
10 Feng H J, Chen L G, Xie Z H and Sun F R 2013 Sci. China: Tech. Sci. 56 299 DOI:10.1007/s11431-012-5097-x [Cited within:1]
11 Feng H J, Chen L G and Sun F R 2012 Sci. China: Tech. Sci. 55 779 DOI:10.1007/s11431-011-4690-8 [Cited within:1]
12 Feng H J, Chen L G, Xie Z H and Sun F R 2014 Int. Commun. Heat Mass Transfer 52 26 DOI:10.1016/j.icheatmasstransfer.2014.01.006 [Cited within:1]
13 Feng H J, Chen L G, Xie Z H and Sun F R 2014 Sci. China: Tech. Sci. 57 784 DOI:10.1007/s11431-014-5494-4 [Cited within:1]
14 Feng H J, Chen L G, Xie Z H and Sun F R 2014 Chin. Sci. Bull. 59 2470 DOI:10.1007/s11434-014-0248-z [Cited within:1]
15 Chen L G, Feng H J, Xie Z H and Sun F R 2013 Int. J. Heat Mass Transfer 67 704 DOI:10.1016/j.ijheatmasstransfer.2013.08.051 [Cited within:1]
16 Zhou B, Cheng X T and Liang X G 2013 Chin. Phys. B 22 084401 DOI:10.1088/1674-1056/22/8/084401 [Cited within:1]
17 Yuan F and Chen Q 2011 Energy 36 5476 DOI:10.1016/j.energy.2011.07.033 [Cited within:1]
18 Cheng X T Liang X G Xu X H 2011 Acta Phys. Sin. 60 060512 (in Chinese) [Cited within:1]
19 Cheng X T and Liang X G 2011 Int. J. Heat Mass Transfer 54 269 DOI:10.1016/j.ijheatmasstransfer.2010.08.026 [Cited within:1]
20 Cheng X T, Zhang Q Z and Liang X G 2012 Appl. Thermal Eng. 38 31 DOI:10.1016/j.applthermaleng.2012.01.017 [Cited within:1]
21 Cheng X T and Liang X G 2012 Energy Convers. Manage. 58 163 DOI:10.1016/j.enconman.2012.01.016 [Cited within:1]
22 Cheng X T and Liang X G 2012 Energy 44 964 DOI:10.1016/j.energy.2012.04.054 [Cited within:2]
23 Cheng X T and Liang X G 2012 Energy 47 421 DOI:10.1016/j.energy.2012.08.041 [Cited within:3]
24 Sun C, Cheng X T and Liang X G 2014 Chin. Phys. B 23 050513 DOI:10.1088/1674-1056/23/5/050513 [Cited within:1]
25 Cheng X T and Liang X G 2013 Chin. Sci. Bull. 58 4696 DOI:10.1007/s11434-013-6096-4 [Cited within:1]
26 Yang A B, Chen L G, Xia S J and Sun F R 2014 Chin. Sci. Bull. 59 2031 DOI:10.1007/s11434-014-0236-3 [Cited within:1]
27 Zhu Y, Hu Z, Zhou Y, Jiang L and Yu L 2014 Energy Convers. Manage. 88 267 DOI:10.1016/j.enconman.2014.07.082 [Cited within:1]
28 Li T, Fu W and Zhu J 2014 Energy 72 561 DOI:10.1016/j.energy.2014.05.082 [Cited within:1]
29 Cheng X T and Liang X G 2014 Int. Commun. Heat Mass Transfer 53 9 DOI:10.1016/j.icheatmasstransfer.2014.02.007 [Cited within:1]
30 Wang W H, Cheng X T and Liang X G 2013 Chin. Phys. B 22 110506 DOI:10.1088/1674-1056/22/11/110506 [Cited within:1]
31 Cheng X T and Liang X G 2013 Energy Buildings 67 387 DOI:10.1016/j.enbuild.2013.08.034 [Cited within:1]
32 Cheng X T and Liang X G 2015 Int. J. Heat Mass Transfer 81 167 DOI:10.1016/j.ijheatmasstransfer.2014.10.026 [Cited within:3]
33 Cheng X T and Liang X G 2014 Energy Convers. Manage. 80 238 DOI:10.1016/j.enconman.2014.01.008 [Cited within:1]
34 Cheng X T and Liang X G 2013 Energy Convers. Manage. 73 121 DOI:10.1016/j.enconman.2013.04.012 [Cited within:1]
35 Bejan A and Lorente S 2012 Chem. Eng. Processing 51 34 DOI:10.1016/j.cep.2012.02.007 [Cited within:7]
36 Bejan A 2014 ASME J. Heat Transfer 136 055501 DOI:10.1115/1.4026527 [Cited within:6]
37 Lucia U 2013 Physica A 392 1051 DOI:10.1016/j.physa.2012.11.027 [Cited within:1]
38 Grazzini G Borchiellini R Lucia U 2013 J. Non-Equilib. Thermodyn. 38 259 DOI:10.1515/jnetdy-2013-0008 [Cited within:5]
39 Grazzini G and Rocchetti A 2014 Energy Convers. Manage. 84 583 DOI:10.1016/j.enconman.2014.04.081 [Cited within:3]
40 Herwig H 2014 ASME J. Heat transfer 136 045501 DOI:10.1115/1.4026188 [Cited within:1]
41 Awad M M 2014 ASME J. Heat Transfer 136 095502 DOI:10.1115/1.4027821 [Cited within:5]
42 Awad M M 2014 Energy Convers. Manage. 88 1070 DOI:10.1016/j.enconman.2014.09.049 [Cited within:7]
43 Manjunath K and Kaushik S C 2014 Renew. Sust. Energ. Rev. 40 348 DOI:10.1016/j.rser.2014.07.186 [Cited within:3]
44 Bejan A 2014 Ind. Eng. Chem. Res. 53 18352 DOI:10.1021/ie5037512 [Cited within:3]
45 Bejan A 2015 Int. J. Heat Mass Transfer 81 654 DOI:10.1016/j.ijheatmasstransfer.2014.10.056 [Cited within:5]
46 Chen Q, Wang M, Pan N and Guo Z Y 2012 Chem. Eng. Processing 56 35 DOI:10.1016/j.cep.2012.02.006 [Cited within:2]
47 Guo Z Y 2014 ASME J. Heat Transfer 136 056001 DOI:10.1115/1.4026528 [Cited within:1]
48 Guo Z Y, Chen Q and Liang X G 2014 ASME J. Heat Transfer 136 046001 DOI:10.1115/1.4026189 [Cited within:1]
49 Chen Q, Guo Z Y and Liang X G 2014 ASME J. Heat Transfer 136 096001 DOI:10.1115/1.4027822 [Cited within:1]
50 Cheng X T and Liang X G 2014 Energy Convers. Manage. 88 1072 DOI:10.1016/j.enconman.2014.10.024 [Cited within:1]
51 Cheng X T and Liang X G 2014 Chin. Sci. Bull. 59 5309 DOI:10.1007/s11434-014-0661-3 [Cited within:2]
52 Wu J and Guo Z Y 2014 Ind. Eng. Chem. Res. 53 18354 DOI:10.1021/ie5040978 [Cited within:1]
53 Xia S J, Chen L G and Sun F R 2008 J. Therm. Sci. Tech. 7 226 [Cited within:1]
54 Chen L, Li J and Sun F 2008 Appl. Energy 85 52 DOI:10.1016/j.apenergy.2007.06.001 [Cited within:1]
55 Chen L, Xia S and Sun F 2009 J. Appl. Phys. 105 44907 DOI:10.1063/1.3082113 [Cited within:1]
56 Cheng X T and Liang X G 2014 Energy Convers. Manage. 87 1052 DOI:10.1016/j.enconman.2014.07.062 [Cited within:1]
57 Cheng X T and Liang X G 2013 Int. J. Heat Mass Transfer 64 903 DOI:10.1016/j.ijheatmasstransfer.2013.05.025 [Cited within:1]
58 Salamon P, Hoffmann K H, Schubert S, Berry R S and Andresen B 2001 J. Non-Equilib. Thermodyn. 26 73 DOI:10.1515/JNETDY.2001.006 [Cited within:2]
59 Cheng X T, Wang W H and Liang X G 2012 Sci. China: Tech. Sci. 55 2847 DOI:10.1007/s11431-012-4915-5 [Cited within:2]
60 Oliveira S R and Milanez L F 2014 Int. J. Heat Mass Transfer 79 518 DOI:10.1016/j.ijheatmasstransfer.2014.08.034 [Cited within:8]
61 Xu M T 2011 Energy 36 4272 DOI:10.1016/j.energy.2011.04.016 [Cited within:1]
62 Guo Z Y 2014 Energy 68 998 DOI:10.1016/j.energy.2014.01.087 [Cited within:1]