†Corresponding author. E-mail: laixianjing@163.com
Compression and stretching of ring-vortex solitons, which is a novel self-similar solution of (2+1)-dimensional diffraction decreasing waveguide, is investigated analytically and numerically. We obtain the ring-vortex solitons via the similarity transformation method. The distance modulation for the width, the diffraction, and the nonlinear response, strongly affects the form and the behavior of the self-similar vortex, and facilitates the efficient compression of optical waves. This approximate ring-vortex solitons can reflect the real properties of self-similar optical vortex beams during propagation under certain parameter window selection. Specific examples and figures are given to illustrate discussed features. The results obtained in this paper may have potential values for all-optical data-processing schemes and the design of beam compressors and amplifiers.
In many branches of physics, self-similarity of waves is a fundamental property that has been explored, [1– 9] such as nonlinear optical systems, Bose– Einstein condensation, plasma physics, fluid dynamics, and condensed matter physics. Self-similar wave profile remains unchanged and its amplitude and width simply vary with time or propagation distance, which implies the delicate balances between the system parameters such as nonlinearity, dispersion or diffraction, gain, inhomogeneity, and external potential of a nonlinear system.
Optical self-similar waves[1, 8, 10] have been studied extensively due to their potential applications in nonlinearity and diffraction management systems, such as nonautonomous systems and the gain amplifier systems. Unlike the standard optical solitons, the amplitude, width, and center of the self-similar solitons can be manipulated by demand, offering the opportunity for light guiding and compression. These solutions are governed by various nonlinear Schr¨ dinger equations (NLSE). The (2+ 1)-dimensional (2D) generalized NLSE has intriguing applications in constructing analytical soliton solutions. Intensive efforts have been devoted to study it because of the experimental controllability of system parameters.[1– 14]
In nonlinear optics, optical vortices are the spatially localized self-trapped modes carrying a nonzero angular momentum, and share many common properties with the vortices observed in other systems.[13– 17] The 2D NLSE gives rise to vortex solitons when the nonlinearity and diffraction are balanced. The experimentally successful demonstrations for vortex solitons in various media, including Kerr, saturable-atomic and photorefractive nonlinear media, [13, 14] stimulate us to investigate the vortex solitons. Probably one of the most interesting features of the vortex physics is the dynamic behavior of vortices. From a short review of the vortex concept, we know that the vortex solitons always experience the symmetry breaking azimuthal instability, and they decay into several fundamental solitons in conservative nonlinear media. However, studies revealed that vortex solitons can be stabilized in some nonlinear media, which include competing nonlinearities, [18] optical lattices, [19– 21] and nonlocality of the nonlinear response, [22] where the vortex symmetry breaking instability is eliminated.
Note that among all of these mentioned above, the study on analytical vortex solitons are less investigated. Thus so far, it is found that the analytical vortex solitons can exist in the presence of external potential when the nonlinearity is self-defocusing. Another approach to finding the analytical vortex solitons relies on the use of the inverse problem.[23] Recently, it was reported that the defocusing spatially inhomogeneous nonlinearity (DSIN) can support analytical vortex solitons, as long as the DSIN strength increases rapidly enough toward the periphery.[15, 16, 24]
The first part of the paper is devoted to construct the ring-vortex solitons with arbitrary values of integer vorticity in 2D inhomogeneous NLSE which describes the propagation of optical beam inside the 2D graded-index waveguide. We believe this kind of optical medium may support more interesting vortices than that in the conventional NLSE with constant self-focusing nonlinearity. By the similarity transformation method, under certain parametric conditions, we reduce the inhomogeneous 2D NLSE into a constant-coefficient one. Then, by making the reverse transformation of variables and functions, we obtain the approximate vortex solution of the inhomogeneous 2D NLSE. Finally, we focus attention on a few particularly selected system parameters, and investigate the propagation properties of the approximate vortex solution numerically.
We construct the analytical vortex soliton solution by considering the following 2D inhomogeneous NLSE:[25]

which describes the propagation of optical beams inside a bulk graded-index nonlinear waveguide amplifier with the refractive index n = n0 + n1f(z)r2 + n2χ (z)I(z, x, y), where I(z, x, y) is the optical intensity, and the dimensionless profile function f(z) can be negative or positive, depending on whether the graded-index medium acts as a focusing (χ > 0) or defocusing (χ < 0) linear lens. Here 


We begin by seeking a similarity transformation
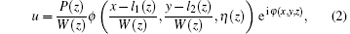
where P(z), W(z), and li(z) (i = 1, 2) represent the power, width, and central positions of the beam, respectively, all of which are the real functions of z. Note that this transformation (2) is different from these transformations in Refs. [11], [25], and [26]. Here ϕ includes three independent variables 
Substituting Eq. (2) into Eq. (1) with

one obtains the 2D NLSE with constant coefficients
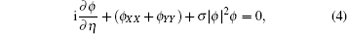
with the following expressions for the width, central positions, effective propagation distance, and phase of the beam:

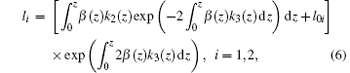
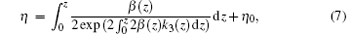


where σ = ± 1 corresponds to self-focusing (+ ) and self-defocusing (− ) nonlinearity of the waveguide, respectively, l0i, k0i, i = 1, 2, and η 0 are the initial values of the corresponding parameters, k1(z), k2(z), and k3(z) are the parameters related to the phase offset, the frequency shift, and the phase-front curvature, respectively, and the phase-front curvature k3(z) is an arbitrary function of z.
Furthermore, the constraints for β (z), f(z), and χ (z) satisfy

Note that the difference between the original equations (1) and (4) is that the latter possesses the z-independent nonlinearity. Thus, we can obtain information on the original equation (1) by investigating Eq. (4) under conditions (3), and (5)– (10).
Next we rewrite Eq. (4) in polar coordinates and obtain

where ρ 2 = X2 + Y2, θ is the azimuthal angle, and η represents the direction of propagation. Function ϕ (ρ , θ , η ) has the form ϕ (ρ , θ , η ) = R(ρ )exp(imθ + iΩ η ), where R(ρ ) is the real envelope and m (integer) is the vorticity, and Ω is a propagation constant. Note that R(ρ ) is the steady-state radial profile which we want to find. Fortunately, employing variational principles in Ref. [27], and substituting β (z), f(z), W(z), ϕ (ρ , θ , η ) into Eq. (2), we can construct the self-similar vortex solution of Eq. (1) in the form



with Eqs. (3), and (5)– (10). Note that an important feature is the universal influence of the phase-front curvature parameter k3(z) on the solutions. It influences not only the form of the amplitude, the phase and the guiding center, but also the width of beam, the spatial frequency shift, and the homogeneous phase shift. Another important feature is that the z modulation for the curvature of the wavefront, the diffraction coefficient β (z), and the profile coefficient f(z), connected through Eq. (10), strongly affects the form and the behavior of self-similar vortex solution. Therefore, we can trap the rate of change of each vortex to control the evolutioin by designing appropriate system parameters.
Also note that the existence of the coefficient f(z) makes the solution more difficult. For f(z) = 0, equation (10) hints k3 = D(z)− 1, where 

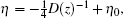
Based on solutions (12) and (13), in the following, major attention will be paid to self-similar vortex solitons in the existence of f(z), and we will graphically analyze the mechanism on how the relevant properties of the optical beam are affected by choosing a different diffraction coefficient β (z).
Firstly, let us pay attention to the compression problem of the laser beam in an exponential diffraction decreasing waveguide with the diffraction according to Refs. [25] and [28]

and the phase-front curvature
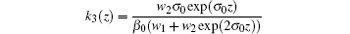
with a small constant gain/loss parameter g = g0. Considering the constraint given by Eqs. (5)– (10), we have






In this system, the initial radius of vortex become larger with increasing vorticity m, and 
Figure 1 displays some evolutional characteristics of the self-similar vortex (Eqs. (12)– (14)), the parameters are taken as Ω = m = 3, w1 = w2 = 4, σ = 1, and P0 = − β 0/2 = l01 = l02 = k01 = k02 = η 0 = 0.5. Here the height and the width of vortex change dramatically. The initial beam is amplified and compressed. From Fig. 1(c), special attention should be paid to the value of σ 0 which determines the vortex speed. It can be seen that the vortex speed changes slowly owing to σ 0 = − 0.01. When σ 0 = − 0.1, figure 1 illustrates the effect of a vortex with the bigger changes as it progresses along the length of the fiber. Moreover, the value of β 0 can influence the change of the vortex. The negative value of β 0 produces the opposite variation pattern (i.e., vortex propagation from right to left direction) of the beam shown in Fig. 1(b) with the positive value of β 0 (i.e., vortex propagation from left to right direction).
 | Fig. 1. (a) Amplitude profiles for several values of vorticity m at z = 0, solutions are given by Eq. (12) with Eqs. (14)– (19); (b) wave center defined by Eq. (17) shown along propagation direction for different β 0; (c), (d) wave height and width defined by Eq. (12) shown along propagation direction for different σ 0 or different g0. Other parameters are Ω = m = 3, w1 = w2 = 4, σ = 1, P0 = l01 = l02 = k01 = k02 = − β 0 = η 0 = 0.5. |
From these scenarios of the height and width in Fig. 1(d), for the gain case g0 = 0.01, the height of the self-similar vortex enhances and the width is compressed along the distance z. While for the loss case of g0 = − 0.01, the height of the vortex attenuates, but it has no effects on the width, and the width is still compressed for the increasing distance z.
Probably one of the most interesting features of the vortex physics is the dynamic behavior of vortices. Presently, the well-developed computer methods give a better insight into the dynamic phenomena. To demonstrate the evolution with respect to finite perturbations for vortex (Eq. (12)) in the diffraction decreasing waveguide with Eq. (14). It is instructive to consider a suitable experimental apparatus, [29] in which we use n0 = 2.7, the graded refractive index n1 = 0.1 cm− 2, and then we obtain the characteristic transverse scale ω 0 ≈ 34 μ m and the diffraction length LD ≈ 3.7 cm near 532 nm. Direct numerical simulations with initial 5% white noise for Eq. (1), with initial fields given by Eq. (12), have been performed. Some evolutional characteristics and propagation dynamics of the corresponding vortex (Eq. (12)) with Eq. (14) is shown in Fig. 2. By numerical estimation, we find that the self-similar vortex soliton given by Eq. (12) is stable for a certain propagation distance in spite of the attenuation determined by the loss parameter. Here, the parameters are chosen as the same as Fig. 1.
 | Fig. 2. (a) Diffraction coefficient β (z), the profile coefficient f(z) and the nonlinear parameter χ (z) change along propagation direction; (b) the central positions, the phase offset, the frequency shift, and the phase-front curvature along propagation direction; (c) self-similar propagation dynamics of the vortex with loss g0 = − 0.01 for the diffraction decreasing waveguide. The initial values are given by Eq. (12) with an added 5% white noise. Other conditions and parameters are the same as Fig. 1. |
Furthermore, for a distributed amplification system with the periodic varying diffraction and nonlinear parameters, β (z) = β 0exp(σ 0z) sin(z).[24] Due to the width function W(z) ≠ 0, variables ki, li, i = 1, 2 and Z are bounded. However, considering the constraint of Eq. (10), if the propagation distance z = nπ , n = 1, 2, 3, … , the parameter of system f is unbounded. Therefore, we cannot discuss further this example in accordance with the similar discussion above.
In real application, due to long-distance communication or manufacturing imperfections, the inhomogeneity always exists, which may result in the fluctuations of waveguide parameters. If the fluctuations are relatively small, one may assume that the waveguide parameters simply fluctuate in a sinusoidal form around the values of the ideal waveguide parameters, that is,

and the phase-front curvature
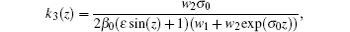
with a small constant gain/loss parameter g(z) = g0. Therefore, we have the other parameters






In Figs. 3(a) and 3(b), attenuation is determined by the loss parameter. We also utilize a split-step beam propagation method and perform direct numerical simulations with initial 5% white noise for Eq. (12) with Eq. (20), where z is the dimensionless coordinate along the propagation direction normalized by LD. Numerical calculations indicate no collapse for this example. Instead, self-similar propagation over hundreds of diffraction lengths is observed in Fig. 3(c) in spite of the fluctuations of waveguide parameters. Here, the parameters are chosen as σ 0 = − 0.01, g0 = − 0.01, w1 = 4, w2 = 8, ε = 0.3, and other parameters are the same as that in Fig. 1.
 | Fig. 3. (a), (b) Parameters of solution defined by Eqs. (20)– (25) shown along propagation direction; (c) self-similar propagation dynamics of the vortex with loss g0 = − 0.01 for the fluctuation of the fiber parameter. The initial values are given by Eq. (12) with an added 5% white noise. Other parameters are the same as Fig. 1. |
In brief, we present, analytically and numerically, self-similar ring-vortex with arbitrary values of integer vorticity of the inhomogeneous NLSE via a similarity transformation connected with the standard NLSE. This vortex soliton solution can reflect the real properties of self-similar optical vortex beams during propagation, although it is approximate. The propagations of the vortex in the diffraction decreasing waveguide have been analyzed in detail and the transmission control used in the diffraction decreasing waveguide has been investigated through choosing different values of the parameters in Eqs. (5)– (9). Considering the fluctuation of the waveguide parameter in real application, we perform direct numerical analysis with initial 5% white noise for the vortex. Numerical studies revealed that spatially localized vortex can be stabilized along certain distances in presence of function f(z) which corresponds to the graded-index waveguide acting as a focusing or defocusing lens. Specific examples and figures are given illustrating discussed features. The study of self-similar vortex solitons in this paper are potentially useful in the areas of planar spatial light modulation, image processing, optical switching, and optical interconnection.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|


