†Corresponding author. E-mail: ibungochouba@rediffmail.com
Hawking radiation of the stationary Kerr–de Sitter black hole is investigated using the relativistic Hamilton–Jacobi method. Meanwhile, extending this work to a non-stationary black hole using Dirac equations and generalized tortoise coordinate transformation, we derived the locations, the temperature of the thermal radiation as well as the maximum energy of the non-thermal radiation. It is found that the surface gravity and the Hawking temperature depend on both time and different angles. An extra coupling effect is obtained in the thermal radiation spectrum of Dirac particles which is absent from thermal radiation of scalar particles. Further, the chemical potential derived from the thermal radiation spectrum of scalar particle has been found to be equal to the highest energy of the negative energy state of the scalar particle in the non-thermal radiation for the Kerr–de Sitter black hole. It is also shown that for stationary black hole space time, these two different methods give the same Hawking radiation temperature.
Hawking discovered the thermal radiation effect of a collapsing black hole by applying the technique of quantum field theory from a given classical black hole, which gives rise to a famous paradox – the information loss paradox in a black hole physics.[1, 2] From the black hole thermodynamics the area of event horizon is taken as entropy and surface gravity may be regarded as temperature.[3– 5] Hawking radiation is a quantum thermal radiation triggered by a vacuum fluctuation near the black hole event horizon. When a virtual pair of particles is created simultaneously just inside the black hole event horizon, the positive energy particle can cross the energy barrier and tunnels to infinity and materializes as a true particle, however the negative energy particle will be absorbed by the black hole and form the Hawking radiation.
Kraus and Wilczek[6, 7] proposed the Hawking radiation as a quantum tunneling process and reinterpreted by Parikh and Wilczek.[8] According to this method, the potential barrier is created by the outgoing particle itself and the imaginary part of the action can be derived by applying the semiclassical WKB approximation. Following this method, Hemming and Keski[9] studied the Hawking thermal radiation effect of an anti de Sitter black hole and Medved[10] investigated the radiation from a de Sitter cosmology. However, in all these investigations, the Painleve coordinates are used to calculate the quantum tunneling effect which has many attractive features. Firstly, the components of the metric in the Painleve coordinates are analytic, not diverging at the event horizon. Secondly, the constant time slices are flat Euclidean spaces. Parikh assumes the second one is important because WKB approximation can be applied to calculate the emission rate and it can be derived from the quantum mechanics of flat space time.[11] Thirdly, there exists a time like a Killing vector field which keeps the space time stationary. The Painleve coordinate system should satisfy Landau’ s coordinate clock synchronization condition.[12]
Zhang and Zhao[13] extended the Parikh method from a static black hole to the massive and charged particles of a non-spherical black hole space time and had a great deal of success.[14– 16] Different from the Parikh method, Angheben et al.[17] proposed the Hawking radiation effect for an extremal and rotating black hole using the relativistic Hamilton– Jacobi equation and WKB approximation without considering the back reaction effect of the emitted particles. Damour and Ruffini[18] and Sannan[19] proposed tortoise coordinate transformation to study the Hawking radiation applying quantum mechanics in curved space time and made much progress.[20– 29]
The organization of this paper is as follows. In Section 2, we study the Hawking radiation of the stationary Kerr– de Sitter black hole in Painleve coordinates using the Hamilton– Jacobi equation. In Section 3, we derive the horizons equation of the non-stationary Kerr– de Sitter black hole utilizing the null hypersurface condition and the generalized coordinate transformation. In Section 4, the Dirac equations are reduced to the first-order form and the second-order form near the horizons using the generalized coordinate transformation and the L’ Hospital rule. The two second-order forms of Dirac equations are transformed to a single form of equation near the horizons. Adjusting the constant parameters, the Hawking radiation effect of a non-stationary black hole is obtained. Separating the wave equation, the chemical potential and Hawking thermal radiation spectra are derived. In Section 5, the thermal radiation spectrum of Dirac particles in a non-stationary black hole is discussed. We derive the expression of the new extra coupling effect and study of the relationship between the thermal and non-thermal black hole as in the scalar particle. Some conclusions are given in the last section.
The line element, describing the Kerr– de Sitter solution with cosmological constant Λ in Boyer– Lindguist coordinates[30] is given by
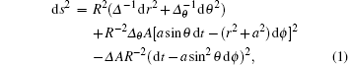
where

Here, Λ is the cosmological constant, while M and a are the mass of the black hole and angular momentum per unit mass. The horizons are determined by
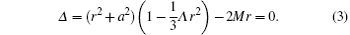
Equation (3) has four roots. We factorize Δ into the following form:
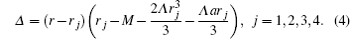
Painleve coordinate For studying the Hawking thermal radiation effect of stationary space time, we perform the following coordinate transformation[31]
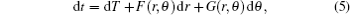
where F(r, θ ) and G(r, θ ) are the two functions to be determined and must satisfy the following integrability condition:

where F(r, θ ) satisfies
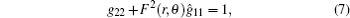
we obtain a new metric (namely Painleve KdS one) as
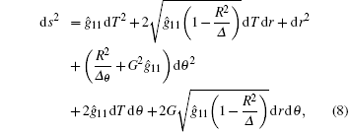
so we obtain

The action I of the outgoing particle satisfies the relativistic Hamilton– Jacobi equation

due to the symmetry of the black hole space time, the separation of variables can be written as follows:
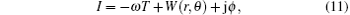
then equation (11) can be written as
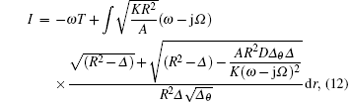
where
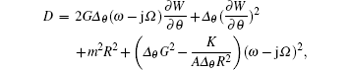
and K = Δ θ (r2 + a2)2− Δ a2sin2θ . The imaginary part of the action at the horizons r = rj can be written as

where 
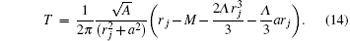
The line element, describing the non-stationary Kerr– de Sitter black hole in the retarded time coordinates (u, r, θ , ϕ )[32] is
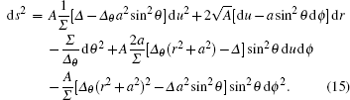
Here, 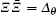

and F(u, r, θ , ϕ ) = 0. The tortoise coordinate transformation technique gives the location and the temperature of the horizon in a non-stationary black hole. The Dirac equations can be transformed to a standard form of wave equation by introducing traditional tortoise coordinate transformation r* = r + (2κ )− 1ln(r − rj) in a non-stationary or stationary space-time (where κ is the surface gravity to be found out) and we assume that the location of the horizons r = rj is a function of retarded time coordinate u. According to Yang et al.[34] and Ibungochouba, [35] the generalized tortoise coordinate transformation is defined by
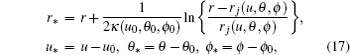
where r = rj(u, θ , ϕ 0) are the location of horizons. All parameters u0, θ 0, ϕ 0 are constant under the generalized coordinate transformation and assumed to be the initial state of the hole. Applying the generalized tortoise coordinate transformation to the null surface condition (16) and taking the limit as r ⟶ rj(u0, θ 0, ϕ 0), u ⟶ u0, θ ⟶ θ 0, and ϕ ⟶ ϕ 0, we obtain
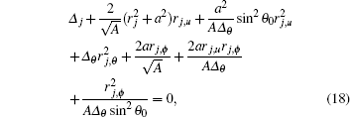
where

The quantities rj, u = ∂ rj/∂ u, rj, θ = ∂ rj/∂ θ , and rj, ϕ = ∂ rj/∂ ϕ are the rates of horizons varying with the time u and different angles θ and ϕ . Equation (18) shows that the shapes of horizons depend on the retarded time u and different angles θ and ϕ due to generalized tortoise coordinate transformation.
The four-coupled Dirac equations[36, 37] in Newman– Penrose formalism are given by
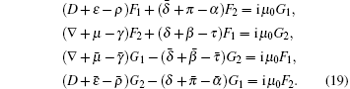
By substituting the various spin-coefficients in Eq. (19), we have

where operators are given by
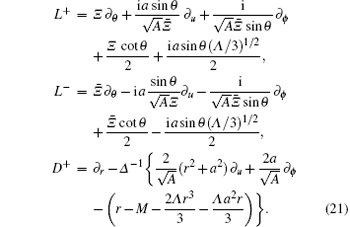
We define F1, F2, G1, and G2 by
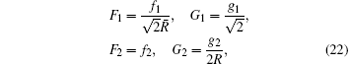
then equation (20) becomes
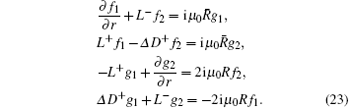
Then, after taking the limit as r ⟶ rj(u0, θ 0, ϕ 0), u ⟶ u0, θ ⟶ θ 0, and ϕ ⟶ ϕ 0, the first-order forms of Dirac equations near the horizon are as follows:
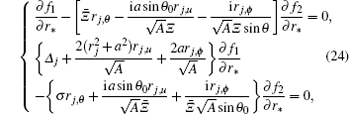
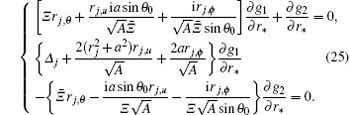
The four derivatives ∂ f1/∂ r*, ∂ f2/∂ r*, ∂ g1/∂ r*, and ∂ g2/∂ r* in Eqs. (24) and (25) are non-zero, then the determinant of their co-efficients is zero. That gives an equation like the null surface condition (18). The second-order forms of Dirac equations near the horizons are given by

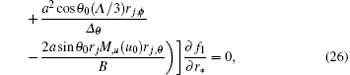

where

In order to obtain the Hawking radiation temperature, the coefficient of 

Then, the surface gravity can be written as

where
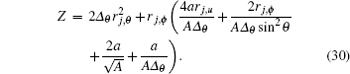
Equations (26) and (28) are transformed into a combined form of wave equation as

with

(i) For Dirac particles Ψ = f1,


(ii) For Ψ = f2,

Following Wu and Cai[20, 21] and Hua and Huang, [22, 28] we may separate the variables in Eq. (31) for the analysis of the field equations as

where Θ (u*, θ *, ϕ *) is an arbitrary real function and ω is the energy of Dirac particles which depend on the tortoise coordinate transformation; Kθ and Kϕ are components of generalized momentum of Dirac particles. Substituting Eq. (35) into Eq. (31) and after separating the variables, we find the radial and angular parts to be given by
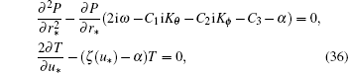
where α is a constant in variable of separation and ζ (u*) is a function of retarded time u* in variable of separation, where

and R(r*, u*) = P(r*)T(u*). The two linearly independent solutions of Eq. (36) near the horizons are given by
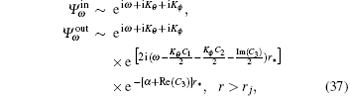
where 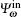

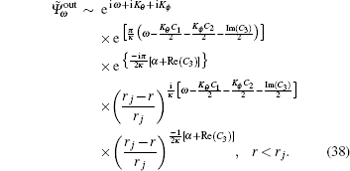
The relative scattering probabilities at r = rj are given by
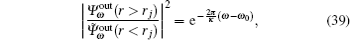
where

According to the suggestion of Damour and Ruffini[18] and extended by Sannan, [19] the thermal radiation spectrum is given by
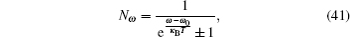
where κ B is the Boltzmann constant and the upper positive symbol stands for the Fermi– Dirac distribution and the lower negative symbol corresponds to the Bose– Einstein statistics. Equation (41) shows that the black hole radiates like a black body. The chemical potential is
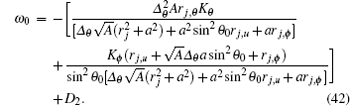
We observe that the constant coefficient D2 appears in the expression of the chemical potential. It may represent a particular energy term for Dirac particles which is absent in the thermal radiation of the other scalar particles. Hawking temperature is given by


From the above, T determines the temperature of the thermal radiation near the horizons r = rj due to the Dirac equations in the non-stationary Kerr– de Sitter black hole. For a stationary black hole, equation (43) can be expressed as
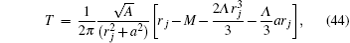
which is equal to the Hawking radiation temperature derived from the relativistic Hamilton– Jacobi equation.
The Klein– Gordon equation of a scalar particle with mass μ in curve space time is given by
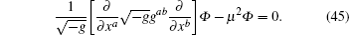
Using generalized tortoise coordinate transformation and applying the same method in Section 4 to Eq. (45) after a tedious calculation, the chemical potential of the scalar particle can be obtained as follows:

Again, utilizing generalized tortoise coordinate transformation in Eq. (10) and defining ∂ Φ /∂ u* = − ω , ∂ Φ /∂ θ * = Kθ , and ∂ Φ /∂ ϕ * = Kϕ , for real ∂ Φ /∂ r*, the maximum energy of the non-thermal radiation[38– 40] can be written as
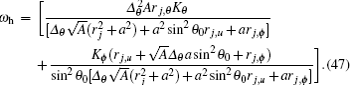
The thermal radiation spectrum (41) implies that the total interaction energy of Dirac particles in a non-stationary Kerr– de Sitter black hole is
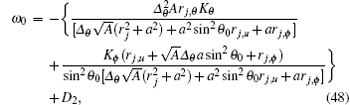
where
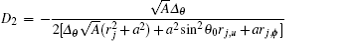

for Ψ = f1, and

for Ψ = f2. The chemical potential ω 0 is composed of two parts. The first part

is the rotational energy arising from the coupling between different components of generalized momentum of Dirac particles and different rotations of black hole. The second term D2 indicates the expression of the new extra spin rotation coupling effect and the spin-acceleration coupling effect which can be written in combined form as follows:
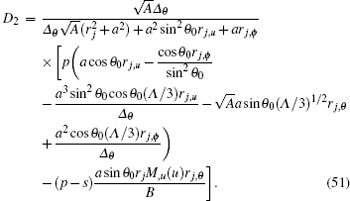
Here,

The value of D2 will vanish for the stationary black hole and other scalar particles. When D2 = 0, equations (47) and (48) indicate that the chemical potential derived from the thermal radiation spectrum of Dirac particles is equal to the highest energy of the negative energy state of scalar particles in non-thermal radiation of Kerr– de Sitter black hole (ω 0 = − ω h). This brings out a clear relationship between the two kinds of radiation processes of black holes.
If we use the traditional tortoise coordinate transformation given in Refs. [20]– [22], [24], and [28], a similar conclusion can be established as Eqs. (42), (46), and (47) but the Hawking radiation temperature effect will be given by
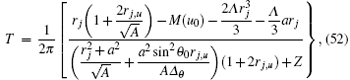
which indicates that the different tortoise coordinate transformations correspond to the different Hawking radiation temperatures in non-stationary black hole space time.[26]
In this paper, we have studied the Hawking thermal radiation effect of the stationary Kerr– de Sitter black hole using the relativistic Hamilton– Jacobi equation and the non-stationary Kerr– de Sitter black hole by applying generalized tortoise coordinate transformation. For the non-stationary space time, the location of horizons, Eq. (18), and the temperature of the black hole, Eq. (43), depend on the retarded time coordinate u and different angles θ and ϕ . The expression of D2 gives the intersection between the intrinsic spin of the particles and generalized momentum of the non-stationary Kerr– de Sitter black hole. However, the value of D2 will vanish for the stationary black hole space time and scalar particles. It reveals that the chemical potential derived from scalar particles is equal to the highest energy of the negative energy state of non-thermal radiation of the Kerr– de Sitter black hole (ω k = − ω h). It is also shown that the Hawking radiation temperature derived from the Hamilton– Jacobi equation is equal to radiation temperature derived from the Dirac equations for the stationary space time near the horizons r = rj.
The author would like to thank Prof. N. Ibohal for suggesting this investigation and the constant encouragement.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|


