As an essential ingredient of any scalable quantum information processor (QIP), ^[1] quantum state transfer (QST) can be applied to the quantum key distribution and quantum teleportation.^{[2, 3]} The transfer of quantum states from one location (A) to another location (B) is accomplished via quantum channels. A physical implementation of such a network could consist of, e.g., trapped atoms or ions with photons providing the quantum channels. Optical systems, typically in quantum communication and cryptography applications, ^{[4, 5]} transfer state from A to B directly via photons which clearly represent the best qubit carrier for fast and reliable communication over a long distance, ^{[6– 8]} since fast and internal-state-preserving transportation of atoms or ions seems to be technically intractable. These photons could contain an actual message or could be used to create entanglement between A and B for future quantum teleportation between the two sites.^[9] Based on the model, some proposals have been proposed.^{[10– 13]} On the other hand, atoms and ions are particularly well suitable for storing qubits in long-lived internal states. Specially, an atomic ensemble with a large number of identical atoms as the basic system is superior to a single particle as a qubit for that the atomic ensemble that contains a large number of identical atoms increases the light– matter coupling strength, which scales with the square root of atomic number involved in the ensemble. This greatly reduces the operation time and thus suppresses the decoherence.

Furthermore, adiabatic techniques are of interest since they feature a certain robustness, and in systems of Λ type one can avoid a transient large population in the excited state. Recently, the techniques of stimulated Raman adiabatic passage (STIRAP)^{[14, 15]} and fractional stimulated Raman adiabatic passage (f-STIRAP)^[16] have been extensively used for realizing the QIP.^{[17– 22]}

In this paper, we present an alternative scheme to implement the QST between two atomic ensembles separately trapped in distant cavities coupled by an optical fiber via adiabatic passage. By choosing appropriate parameters of the system, two atomic ensembles interact with “ the same cavity mode” . Under adiabatic condition, by adjusting the laser frequencies applied to the atomic ensembles, the state of atomic ensemble A can be transferred to atomic ensemble B. The process is insensitive to the deviation of atomic number in each ensemble and the coupling coefficient between the atoms and cavity modes. It does not need to control the evolution time and pulse parameters accurately. In addition, based on the effective Hamiltonian, the atoms are always in the ground states and the cavity modes on the vacuum state during the evolution, so spontaneous emission and cavity decay can be efficiently suppressed. The present scheme can be used to implement the QST between two arbitrary atomic ensembles in the multi-atomic-ensemble network.

The paper is organized as follows. In Section 2, we first describe the model under consideration and then simplify it into an effective form. In Section 3, we then present the implementation of QST between two atomic ensembles via adiabatic passage. In Section 4, we discuss the influence of experimental parameters on the fidelity of QST. In Section 5, we show the idea that can be used to realize the QST between two arbitrary atomic ensembles in the multi-atomic-ensemble network and discuss the experimental feasibility of the proposed scheme. We finally present our conclusions in Section 6.

Let us first briefly describe the dynamical model of our considered system. Two atomic ensembles (labeled A and B) are separately trapped in two cavities coupled by an optical fiber. Suppose that the two cavity modes are resonant with the fiber mode with the coupling strength ν . In the interaction picture, the resonant coupling between the two cavity modes and the fiber mode is given by the interaction Hamiltonian H₀ = ν b⁺ (a₁ + a₂) + H.c., ^[23] where a_i (i = 1, 2) is the annihilation operator for the ith cavity mode and b⁺ is the creation operator for the fiber mode. The atomic number in the ith cavity is N_i. Each atom has an excited state | e⟩ and two ground states | f ⟩ and | g⟩ . The atomic transition | e⟩ _i ↔ | g⟩ _i is coupled to the cavity mode a_i with coupling coefficient g_i and detuning Δ _gi. Meanwhile, the atoms are driven by a classical laser field with the Rabi frequency Ω _i and detuning Δ _i (i = 1, 2). In the interaction picture, the Hamiltonian describing atom– field interaction is (ħ = 1)

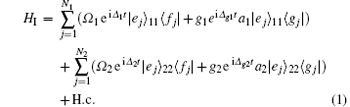
Introducing the new bosonic modes , , and , ^[23] we can rewrite H₀ as . In terms of the bosonic mode c_k (k = 1, 2, 3), the Hamiltonian H₀ is diagonal, so we can take H₀ as the “ free Hamiltonian” mathematically and perform the transformation e^iH₀t to obtain the atom– field interaction Hamiltonian in the interaction picture. In this case, the Hamiltonian H_I can be rewritten as

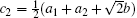
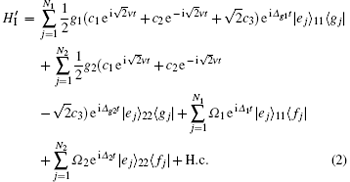
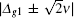
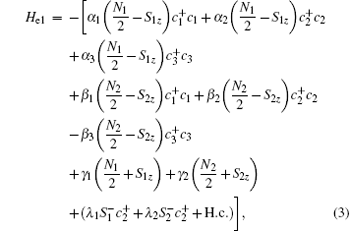
In the case that Δ ₁, Δ ₂, , , ν ≫ g₁, g₂, Ω ₁, Ω ₂, the upper-level | e⟩ can be adiabatically eliminated. Choose the detunings appropriately so that the dominant Raman transitions are induced by the the classical fields and bosonic mode c₂, while the probability of the coupling between the classical fields and bosonic mode c_k (k = 1, 3) is negligible due to a large detuning. This leads to the effective Hamiltonian

where

We have set . The first six terms of the Hamiltonian correspond to the photon-number-dependent Stark shift for the state | g⟩ induced by bosonic modes c₁, c₂, and c₃. The next two terms correspond to the Stark shift for | f ⟩ induced by classical fields. The last two terms describe the coupling between atomic operators and and bosonic mode c₂. After the Holstein– Primakoff transformation, ^{[24, 25]} the collective atomic operators (, , S_1z, S_2z) are associated with the bosonic annihilation operators A and B and creation operators A⁺ and B⁺ via

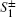
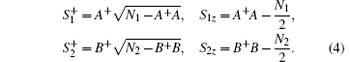
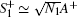
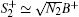
When the average number of atoms in the state | f⟩ is much smaller than the total number, i.e., A⁺ A ≪ N₁ and B⁺ B ≪ N₂, the collective atomic operators are well approximated by , , S_1z≃ − N₁/2, and S_2z≃ − N₂/2. The effective Hamiltonian reduces to

We rewrite H_e2 as H_e2 = H₀ + H₁, with and . We then perform the further transformation e^iH₀t of H₁ to obtain the new engineered Hamiltonian

where ω = N₁α ₂ + N₂β ₂, 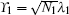, and .

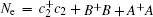
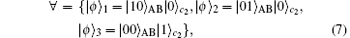
Define the excitation number operator . N_e commutes with H_e3 so that the excitation number is conserved during the evolution. The subspace ∀ with N_e = 1 is spanned by the state vectors

where | xy⟩ _AB| z⟩ _c2 (x, y, z = 0, 1) denotes the x-excitation and y-excitation states of the collective atomic modes A and B, and z-excitation state of the bosonic mode c₂. The Hamiltonian H_e3 has the following dark state:

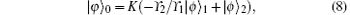
where .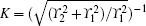

Now we proceed to show the implement of QST from atomic ensemble A to atomic ensemble B via adiabatic passage of the dark state, i.e., (a| 0⟩ _A + b| 1⟩ _A)| 0⟩ _B → (a| 0⟩ _B + b| 1⟩ _B)| 0⟩ _A, where | a| ² + | b| ² = 1. As the initial state of the whole system is | ϕ ⟩ ₀ = (a| 0⟩ _A + b| 1⟩ _A)| 0⟩ _B, the state | 00⟩ _AB| 0⟩ _c2 remains unchanged, while the state | 10⟩ _AB| 0⟩ _c2 will evolve within the subspace in Eq. (7) during the adiabatic process. In our scheme, we choose the parameters to satisfy

Then, based on Eq. (8), we can adiabatically transfer the state | 10⟩ _AB| 0⟩ _c2 to | 01⟩ _AB| 0⟩ _c2 with | 00⟩ _AB| 0⟩ _c2 unchanged, i.e., (a| 0⟩ _A + b| 1⟩ _A)| 0⟩ _B → (a| 0⟩ _B + b| 1⟩ _B)| 0⟩ _A. In this paper, we set N = 10², Δ ₁ = Δ ₂ = Δ = 100g, Δ _g1 = Δ _g2 = Δ g = 200g, then the parameter values ω = g/2, ϒ ₁ = Ω ₁/20, and ϒ ₂ = Ω ₂/20. That is, the Rabi frequency Ω ₁ is initially zero while Ω ₂ is larger than zero. Then, reduce Ω ₂ and simultaneously increase Ω ₁ adiabatically until Ω ₂/Ω ₁ → 0. As a result, we adiabatically realize the QST, i.e., (a| 0⟩ _A + b| 1⟩ _A)| 0⟩ _B → (a| 0⟩ _B + b| 1⟩ _B)| 0⟩ _A.

The time-dependent Rabi frequencies of the laser fields which satisfy our scheme can be obtained with Gaussian envelopes, which are given by

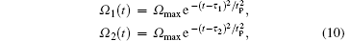
where Ω _max, t_p, and τ _i (i = 1, 2) are the peak, the width, and the time delay of the laser pulses, respectively. Figure 1 shows the fidelity versus the dimensionless parameter gt, where we choose Ω _max = 30g, t_p = 50/g, τ ₁ = 160/g, and τ ₂ = 80/g. We see that the fidelity reaches unit one, which means that the numerical results show good agreement with the expected results. Furthermore, the figure confirms that the time need not to be controlled strictly. In the following calculation, we choose T = 200/g as the evolution time. The purpose of our scheme is to realize the QST between two atomic ensembles with a high fidelity via adiabatic passage. Here, the fidelity is defined by F = ⟨ ψ (t)| ψ _ideal⟩ ², where | ψ (t)⟩ is the final state which is governed by the Schrö dinger equation in the system, and | ψ _ideal⟩ is the ideal target state (a| 0⟩ _B + b| 1⟩ _B)| 0⟩ _A. In Fig. 2, we plot the dependences of the fidelity of the QST on the parameters of the classic field, i.e, Ω _max (a), t_p (b), τ ₁ and τ ₂ (c). As can be seen from three subfigures, the fidelity is larger than 0.99 when the parameters are set in a large range. We also observe from Fig. 2(b) that the fidelity is unstable when t_p < 40/g or t_p > 60/g. The reason is that the large deviation cannot ensure the initial condition and the final condition in Eq. (9) perfectly. In STIRAP, the Stokes pulse linking the final state comes first and is followed after a certain time delay by the pump pulse linking the initial state, i.e., τ ₁ > τ ₂. Figure 2(c) illustrates that the fidelity decreases rapidly when τ ₁ − τ ₂ increases. Obviously, Ω ₂/Ω ₁ → ∞ can not be satisfied at the end of evolution when τ ₂ is close to τ ₁. Hence, a high fidelity of the QST can be obtained as long as the experimental parameters are set in a reasonable range. Moreover, we plot Fig. 3 to show the fidelity versus the number of atoms in each ensemble. It demonstrates that the fidelity is larger than 0.99 as long as N > 10. On the other hand, the larger the number of atoms is, the more effective the Hamiltonian in Eq. (6) is. We choose N = 100 in this paper. In the above analysis, we assume that all atoms in the same cavity have the same coupling strength to the cavity fields. However, this assumption is difficult to achieve in practice because the atom– cavity coupling strength is dependent on the atomic position in the cavity and may fluctuate. It is necessary to check how the errors in the coupling influence the fidelity of QST. In Fig. 4, we show the variation of the fidelity when δ g changes in a wide range, where δ g is the deviation from the ideal atom– cavity coupling coefficient. We note that the deviation of g in the same cavity has a negligible influence on the fidelity of QST because the condition is almost unaffected when the fluctuation of g happens. Therefore, the scheme is robust against the fluctuations of some parameters. 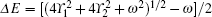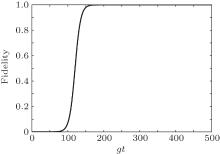For the implement of the QST, the adiabatic approximation requires that Δ ET ≫ 1, ^[26] where is the minimum energy gap between the dark state and the bright states of the Hamiltonian H_e3. To verify that our scheme satisfies the adiabatic condition, we plot Fig. 5 to depict the relationship between Δ ET and gt with the above given parameters. We can see from Fig. 5 that at the beginning of evolution Δ ET ≃ 20, which meets the adiabatic conditions. As the evolution proceeds, the condition Δ ET ≫ 1 is always satisfied. Thus, the adiabatic condition can be well satisfied during the whole evolution.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. The fidelity versus the dimensionless parameter gt with Ω max = 30g, tp = 50/g, τ 1 = 160/g, and τ 2 = 80/g. The other parameters are N = 100, Δ = 100g, and Δ g = 200g.

Fig. 2.

	Figure Option ViewDownloadNew Window
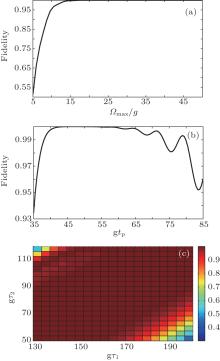	Fig. 2. (a) The fidelity versus Ω max/g with τ 1 = 160/g, τ 2 = 80/g, and tp = 50/g. (b) The fidelity versus tp with Ω max = 30g, τ 1 = 160/g, and τ 2 = 80/g. (c) The fidelity versus τ 1 and τ 2 with Ω max = 30g and tp = 50/g. The other parameters are the same as those in Fig. 1.

Fig. 3.

	Figure Option ViewDownloadNew Window
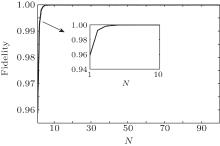	Fig. 3. The fidelity versus N with the same parameters as those in Fig. 1.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. The fidelity versus δ g with the same parameters as those in Fig. 1.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Δ ET versus the dimensionless parameter gt with the same parameters as those in Fig. 1.

We note that the above idea can be used to realize the QST between two arbitrary atomic ensembles in the multi-subsystem network. We consider that n atomic ensembles (labeled as 1, 2, 3, … , n) are trapped in each of the distant cavities (labeled as c₁, c₂, c₃, … , c_n) collectively connected to a single-mode integrated optical cavity c₀ which traps a atomic ensemble (labeled as 0) via optical fiber coupler, as shown in Fig. 6. This model has been studied in Refs. [27]– [29]. Assuming that all the fibers connected to the coupler have the same transverse mode. 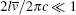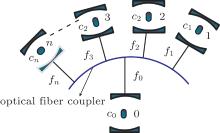In the short fibre limit, , where l is the length of the fiber and is the decay rate of the cavity fields into a continuum of the fiber modes, and only one resonant mode of the fiber interacts with the cavity modes. Let us suppose that the purpose is to achieve the QST from atomic ensemble x (x ≤ n) to atomic ensemble y (y ≤ n and y ≠ x), i.e., (a| 0⟩ _x + b| 1⟩ _x)| 0⟩ _y→ (a| 0⟩ _y + b| 1⟩ _y)| 0⟩ _x, where | a| ² + | b| ² = 1. That is, the atomic ensemble x is first prepared in the state a| 0⟩ _x + b| 1⟩ _x and the other atomic ensembles in the state | 0⟩ . We adjust the cavity modes c₀, c_x to resonate with the fiber mode. The interaction Hamiltonian describing the fiber– cavity is H_cfx = ν b⁺ (a₀ + a_x) + H.c., where b⁺ is the creation operator for the fiber mode. As described above, we implement the QST from atomic ensemble x to atomic ensemble 0 via adiabatic passage of dark state, i.e., (a| 0⟩ _x + b| 1⟩ _x)| 0⟩ ₀ → (a| 0⟩ ₀ + b| 1⟩ ₀)| 0⟩ _x. Next, we adjust the cavity modes c₀, c_y to resonate with fiber mode. Now, the interaction Hamiltonian describing the fiber– cavity is H_cfy = ν b⁺ (a₀ + a_y) + H.c.. The next step is to implement the QST from atomic ensemble 0 to atomic ensemble y via adiabatic passage of dark state using the same method as the above one, i.e., (a| 0⟩ ₀ + b| 1⟩ ₀)| 0⟩ _y → (a| 0⟩ _y + b| 1⟩ _y)| 0⟩ ₀. That is, we achieve (a| 0⟩ _x + b| 1⟩ _x)| 0⟩ _y → (a| 0⟩ _y + b| 1⟩ _y)| 0⟩ _x.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. n atomic ensembles are trapped in each of the distant cavities connected to a single-mode integrated optical cavity by fibers.

Now let us briefly discuss the experimental feasibility of the proposed scheme. The required atomic level configuration can be achieved in cesium atom.^{[30, 31]} Three atomic states | e⟩ , | f ⟩ , and | g⟩ correspond, respectively, to | F = 4, mf = 3⟩ hyperfine state of 6²P_3/2, | F = 3, mf = 2⟩ hyperfine state of 6²S_1/2, and | F = 3, mf = 4⟩ hyperfine state of 6²S_1/2. Experiments with cesium atoms have been at the forefront of quantum information processing. Additionally, a single cesium atom can be localized at a fixed position in each cavity with a high precision for a long time.^[32] According to Ref. [33], the no-direct-interaction condition can be satisfied very well when the number of atoms of each ensemble is less than 200, and all the atoms in the cavity collectively interact with the cavity field with the nearly same coupling strength. Thus, the assumption that all the atoms in the cavity have the nearly same coupling strength and collectively interact with the cavity field is valid. Furthermore, we have verified that some deviation of the atom– cavity coupling strength which depends on the atomic position in the cavity has a weak influence on the fidelity of the QST. The nearly perfect cavity– fiber coupling with an efficiency larger than 99.9% has been reported, ^[34] and a technique of using a 1 × n fiber optical coupler as a distributed strain sensor in a white-light interferometer is presented.^[35] In Ref. [36], the coupler has been realized by using a planar arrangement of two confocal arrays of radial waveguides performing with efficiency approaching 100% under ideal conditions, when the waveguides have strong mutual couplings. In our proposal, the atoms are virtually excited during the evolution, and the effective decoherence rate due to the atomic spontaneous emission is 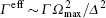, ^{[37– 39]} where Γ is the atomic spontaneous emission rate. The leakage error to the bright eigenstates is , where is the average value of Δ E.^[39] This leads to the effective decoherence rate arising from the cavity decay κ ^eff = κ P_c, where κ denotes the cavity decay rate. Taking the cavity parameters g = 2 × 10⁹ Hz, Γ = 1.6 × 10⁷ Hz, and κ = 0.4 × 10⁵ Hz, ^{[40, 41]} the infidelity induced by the decoherence is on the order of (κ ^eff + Γ ^eff)T ∼ 0.1. Therefore, the decoherence can be perfectly suppressed.

In conclusion, we have proposed a scheme for quantum state transferring between atomic ensembles separately trapped in two distant cavities via adiabatic passage of dark state. By numerical calculations, we have verified that experimental parameters are allowed to fluctuate moderately. It should be noted that the interaction time needs not to be adjusted very accurately as long as the adiabatic condition is satisfied. In addition, the effective decoherence can be suppressed effectively. In the last section, we have briefly discussed the experimental feasibility of the proposed scheme. Based on the cavity QED techniques presently or soon to be available, the scheme might be realizable.