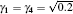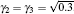†Corresponding author. E-mail: shengyb@njupt.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 11474168 and 61401222), the Qing Lan Project in Jiangsu Province, China,and the Priority Academic Development Program of Jiangsu Higher Education Institutions, China.
We propose a protocol for directly measuring the concurrence of a two-qubit electronic pure entangled state. To complete this task, we first design a parity-check measurement (PCM) which is constructed by two polarization beam splitters (PBSs) and a charge detector. By using the PCM for three rounds, we can achieve the concurrence by calculating the total probability of picking up the odd parity states from the initial states. Since the conduction electron may be a good candidate for the realization of quantum computation, this protocol may be useful in future solid quantum computation.
Quantum entanglement plays an important role in quantum information and computation. Quantum teleportation, [1] quantum key distribution (QKD), [2– 6] quantum secure direct communication (QSDC), [7– 15] and some other quantum communication protocols[16– 21] all require entanglement. In many schemes for the quantum information processing, the maximally entangled states or partially entangled states with determined degree of entanglement is needed to act as channel. Therefore, how to establish efficient ways to estimate the degree of entanglement is a very crucial task and has attracted widespread interest. In recent years, several methods have been proposed to detect and measure entanglement.[22– 33] On one hand, the protocols which work via indirect measurement are proposed. For instance, a simple method to estimate the degree of entanglement is quantum state tomography.[26, 28, 34] One must reconstruct the density matrix by a complete set of observations for the purpose to evaluate the entanglement in the experiment. The disadvantage of this method is that the number of measured observations grows rapidly with the size of the system, so that it is only suitable for small quantum systems. Entanglement witness is another important indirect method for entanglement detection, [35] which needs the priori knowledge of the detected state.
In 1996, Bennett et al. proposed a concept called entanglement of formation (EOF) to quantify entanglement.[36] Subsequently, it was proved that the EOF of an arbitrary two-qubit state ρ is related to concurrence, [37, 38] which can be defined as
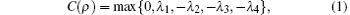
where λ i (i = 1, 2, 3, 4) are the non-negative eigenvalues in decreasing order of the Hermitian matrix 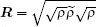
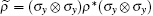

can be simply written as[38, 39]
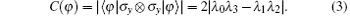
In 2006, the first direct experimental evaluation of entanglement was proposed by Walborn et al.[40] Their protocol requires the hyperentanglement to measure the concurrence of the entanglement in polarization. Many other protocols were proposed for different systems.[41– 45] For example, Romero et al. proposed an protocol to measure the concurrence for an arbitrary atomic two-qubit pure state in three-dimensional microwave cavities.[41] Zhang et al. discussed measurement of the concurrence for a two-photon polarization entangled pure state with the help of cross-Kerr nonlinearity.[43, 44] Recently, the approach of measuring the concurrence for atomic entanglement was proposed.[45]
On the other hand, it is known that conduction electron is a good candidate for the realization of quantum computation. In 2004, Beenakker et al. designed a complete controlled-not (CNOT) gate based on the charge qubit.[46] An electron system has both charge degree of freedom and spin degree of freedom, which can be operated independently. That is to say, if one measures the charge degree of freedom with the charge detector, [47] the spin degree of freedom will not be affected. Subsequently, many quantum information processing protocols were proposed, such as entanglement purification, [48– 50] entanglement concentration, [51– 57] the generation of the cluster states, [58, 59] hyperentanglement Bell-state analysis, [60, 61] and the measurement-based quantum computation scheme from spin systems to fermion systems.[62]
As the entanglement encoded in conduction electron plays an important role in current quantum information processing, in this paper, we will describe an alternative approach to measure the concurrence of the entanglement. This paper is organized as follows. In Section 2, we introduce the key element of this protocol, say the parity-check measurement (PCM) gate for two-qubit electron states. In Section 3, the protocol for direct measurement of the concurrence for two-qubit electron states will be presented. In Section 4, we present the discussion and conclusion.
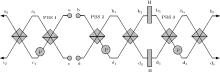
In our protocol, we exploit two polarization beam splitters (PBSs) and a charger detector to complete the task, as shown in Fig. 1.[46] For the case of two electrons, there are four different cases of the two electrons in modes a and b, such as | ↑ ⟩ a| ↑ ⟩ b, | ↑ ⟩ a| ↓ ⟩ b, | ↓ ⟩ a| ↑ ⟩ b, and | ↑ ⟩ a| ↑ ⟩ b. Here | ↑ ⟩ is the spin up and | ↓ ⟩ is the spin down of the electron, respectively. Therefore, an arbitrary two-electron spin entangled pure state can be written as
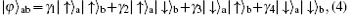
with | γ 1| 2+ | γ 2| 2+ | γ 3| 2+ | γ 4| 2 = 1. From Fig. 1, the electronic PBS can make the | ↑ ⟩ polarized electron be fully transmitted and the | ↓ ⟩ polarized electron be fully reflected, respectively. The states | ↑ ⟩ a| ↑ ⟩ b and | ↓ ⟩ a| ↓ ⟩ b will make both the spatial modes a′ and b′ contain one electron, respectively. The state | ↑ ⟩ a| ↓ ⟩ b will make the spatial mode b′ get two electrons and the state | ↓ ⟩ a| ↑ ⟩ b will make the spatial mode a′ get two electrons. Taking the result of the charger detector into consideration, the case of one electron can be distinguished from the case of 0 or 2 electrons.[46] The cases of 0 or 2 electrons cannot be distinguished. To ensure the two output ports of the PBS have and only have one electron, we introduce another PBS. Let the electrons in spatial modes a′ and b′ pass through the second PBS. We take the devices in Fig. 1 as a entirety and denote them as PCM. For the four different cases of two electrons incident onto the PCM, we can distinguish them into odd parity states | ↑ ⟩ a| ↓ ⟩ b and | ↓ ⟩ a| ↑ ⟩ b and even parity states | ↑ ⟩ a| ↑ ⟩ b and | ↓ ⟩ a| ↓ ⟩ b, respectively.
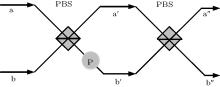 | Fig. 1. Schematic diagram showing the principle of parity check measurement (PCM).[46] The two electron spin entangled states in spatial mode a and b pass through the first PBS, which will make the charger detector detect 0, 1, or 2 electrons. We can divide them into odd parity and even parity, which will be useful in our protocol. The second PBS is used to ensure that the two out ports (a″ and b″ ) own one electron, respectively. |
Let us consider two copies of two-qubit entangled states which are in spatial modes a and b, c and d, respectively. They have the same form as Eq. (4). We can describe the initial joint state of the four electrons as

As shown in Fig. 2, we let the electrons in spatial modes a and c pass through PBS1 to make a PCM. If P shows no electron, the initial states will become the following state:

where N1 = 2(| γ 1| 2+ | γ 2| 2)(| γ 3| 2+ | γ 4| 2). The possibility of getting the states in Eq. (6) from the initial states in Eq. (5) can be denoted as P1 = N1. To ensure the output ports a2 and c2 have and only have one electron, we let the electrons in modes a1 and c1 pass through another PBS, as shown in Section 2. Equation (6) becomes

Subsequently, we let the electrons in spatial modes b and d pass through the PBS2. We also pick up the cases that P shows 0 (2) electrons, and then the state in spatial modes b2 and d2 will be
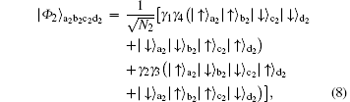
where N2 = 2(| γ 1| 2| γ 4| 2+ | γ 2| 2| γ 3| 2). The possibility of getting the states in Eq. (8) from the states in Eq. (7) can be denoted as P2 = N2/N1. We perform an Hadamard operation on the electrons in spatial modes b2 and d2, instead of letting them directly pass through the PBS3. The Hadamard operation will make 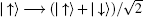
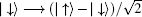
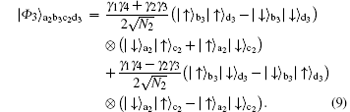
To complete the task of getting the concurrence, we let the electrons in spatial mode b3 and d3 pass through the PBS3 to make a PCM again. If we pick up the case that P shows 0 (2) electrons, we can obtain the state as
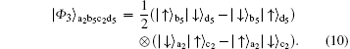
We can have P3 = (| γ 1γ 4| − | γ 2γ 3| )2/N2 which represents the possibility. Finally, we can obtain the state in Eq. (10) from the initial states of the four electrons with a total probability Ptotal as
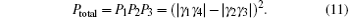
Based on Eqs. (3) and (11), we can obtain the concurrence of the state | φ ⟩ as
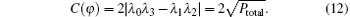
From the above description, in order to obtain the concurrence of the initial state, we should perform the PCM for three rounds. In each round, our aim is to pick up the odd parity state from the states. If the measurement result in one of the three PCMs is even parity, this protocol fails and we restart the protocol. In this way, the measurement of the concurrence can be transformed to obtain the success probability of the three PCMs directly.
From Eq. (10), the lower concurrence means that we have lower probability to obtain the states in Eq. (10), which has been considered as success of that round of protocol. We should point out that, the probability of obtaining the states in Eq. (10) is not equal to the probability of obtaining the concurrence. Since once we get the probability of obtaining the states in Eq. (10), the concurrence of the initial state is nearly determined. It is clear that the concurrence of the state is encoded in the success probability of getting Eq. (10) rather than the state itself.
We have proposed a method for the purpose to directly measure the concurrence of electronic entangled state. It is obvious that the key elements for realizing this protocol is the electronic PBS and the charge detector. With the help of electronic PBS and charge detector, we can perform the complete PCM. However, in a practical experiment, we should consider the error of such PCM. It may come from the error measurement of the charge detector. For example, if an error occurs, the odd parity state | ↑ ⟩ | ↓ ⟩ or | ↓ ⟩ | ↑ ⟩ will make the charge detector show 0 (2). Suppose that such error probability is Perror1. On the other hand, if the initial state is even parity state | ↑ ⟩ | ↑ ⟩ or | ↓ ⟩ | ↓ ⟩ , it will make the charge detector show 1. However, the error will make it show 0 (2). Suppose such error probability is Perror2. Taking the error probability (Perror1 and Perror2) into consideration, we can recalculate the probability Ptotal as Perror which can be described as
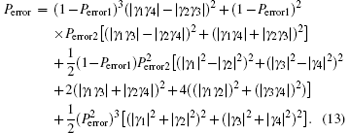
We denote the relative success probability as Q = Perror/Ptotal. To illustrate the relationship between Q and the error probability (Perror1 and Perror2), we let the coefficients of the initial state be specialization, as shown in Fig. 3. Interestingly, such errors will make Q > 1, which means that the errors will increase the concurrence.
Finally, let us briefly discuss the realization of electronic PBS and charge detector in experiment. In 2003, a protocol for such a device was designed by Ionicioiu and Amico.[63] They used nondispersive phases to separate spin up and spin down which carries into distinct outputs and made it analogous to a Stern– Gerlach apparatus. The charge detection has been realized in a two-dimensional electron gas. Current experiment reported that currently achievable time resolution for charge detection is μ s.[64] In a semiconductor, it was shown that the resolution required for ballistic electrons is less than 5 ps.[65]
In conclusion, we have proposed a protocol for the direct measurement of the concurrence for two-qubit electronic pure entangled states. We perform the PCM for three rounds. We show that the measurement of concurrence can be transformed to measure the success probability of the PCM. By repeating this protocol for many rounds, we can obtain the concurrence directly. As the conduction electron may be a good candidate for the realization of quantum computation, this protocol may be useful in future solid quantum computation.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|
| 51 |
|
| 52 |
|
| 53 |
|
| 54 |
|
| 55 |
|
| 56 |
|
| 57 |
|
| 58 |
|
| 59 |
|
| 60 |
|
| 61 |
|
| 62 |
|
| 63 |
|
| 64 |
|
| 65 |
|