One of the most challenging problems facing contemporary science and engineering is to realize a large-scale quantum computation (QC).^{[1– 4]} A serious obstacle to the large-scale QC is the limit on the number of coupled qubits that can be achieved in a physical system. As the physical realization of QC comes closer, the interest in distributed quantum computation (DQC)^[5] is steadily growing. A distributed quantum computer can be viewed as a multi-processor device where each processor contains only a small number of qubits and acts as a node of quantum network on which many recent studies have been reported.^{[6– 8]} In DQC, collective unitary operations often need to be implemented on qubits at distant nodes. We call this operation a nonlocal one. Efficiently implementing a nonlocal quantum operation using as few resources of local operations, classical communications, and shared entanglements (LOCCSEs) as possible is critical in DQC as it reduces not only the resources, but also the errors. Recently, a number of fundamental research on implementing locally a nonlocal quantum operation appeared and made some interesting progress both in theory and in experiment.^{[9– 15]} On the other hand, how to create effectively as much entanglement as possible by nonlocal quantum operations performed on multi-particle states has also been investigated.^{[9, 16]}

“ If both c₁ and c₂ are true, then do t.” This is one of the most useful types of controlled operation in QC. Suppose {V_i, i = 1, 2, … , N} is a set of arbitrary single-qubit unitary operations. The N-target controlled-controlled gate is defined to have two control qubits {c_j, j = 1, 2} and N target qubits {t_i, i = 1, 2, … , N}, and performs respectively the given unitary operations V₁, V₂, … , V_N on individual target qubits t₁, t₂, … , t_N if and only if both the c₁ and c₂ are set | 1〉 . may be constructed by concatenating N single-target controlled-controlled gate

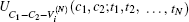
where

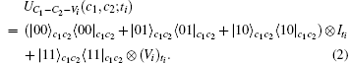
The N-target controlled-controlled gate is an indispensable ingredient in both the quantum algorithm^{[1, 17]} and the quantum errors-correction protocols.^{[1, 18]} If N = 1 and V = X (here, and in what follows, we will write X and Z instead of σ _x and σ _z), it corresponds to the familiar Toffoli gate. It is proved that the Toffoli gate is universal for QC if the single-qubit Hadamard gate is provided as free resource.^[1]

The method of implementing locally a nonlocal single-target controlled– controlled gate of Eq. (2) was firstly proposed by Eisert et al. in 2000, and they showed that two local two-body CNOT gates and a local three-body controlled– controlled gate supplementing by two Bell states^[1] and four feed-forward corrections are necessary for implementing locally this nonlocal gate.^[10] It is noteworthy that Eisert et al.’ s scheme involves a local three-body interaction. From an experimental point of view, this will not appear naturally. Of course one could employ the simulation of the gate with the use of single- and two-body gates as in Refs. [19]– [21]. It has been proven that any three-body controlled– controlled gate can be implemented by using five two-body gates circuit.^[19] So if we implement the nonlocal (N+ 2)-body gate 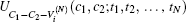with N nonlocal three-body controlled– controlled gates {U_{C1− C2− Vi}(c₁, c₂; t_i)} one after the other as shown in Eq. (1), then at least 2N Bell states, 7N local two-body CNOT gates, four cbits (classical bits), and 2N feed-forward corrections are required for Eisert et al.’ s scheme.

It is well known that multipartite entangled states like the GHZ states and the W states are also very important entanglement resource and are better suit for certain quantum communication and computation (QCC) tasks.^{[13, 22– 27]} The present paper is concerned with the local implementation of a nonlocal N-target controlled– controlled operation via GHZ channel. Following some ideas of Refs. [12] and [28], we demonstrate that if each target node harnesses a qutrit as a catalysator, the nonlocal (N + 2)-body gate of Eq. (1) can be implemented more efficiently.

Suppose (N + 2) users C₁, C₂, T₁, T₂, … , T_N are localized in different space nodes of a quantum network. Each of them holds a qubit in an arbitrary state | j〉 = a_j| 0〉 _j + b_j| 1〉 _j (j = c₁, c₂, t₁, … , t_N). The state of (N + 2) message qubits, which the nonlocal operation of Eq. (1) will perform on, can be expanded as

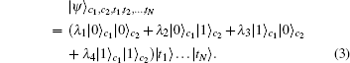
In the following, we will present a scheme that allows C₁, C₂, T₁, … , T_N to perform locally the nonlocal gate (1) on the state (3), i.e., transform it to

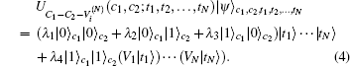
To begin with, the (N + 2) users need to share two (N + 1)-qubit GHZ states

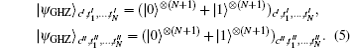
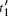
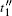
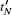
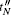
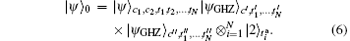
Here, and in what follows, we leave out normalization factors for states. We give respectively particles c′ , c″ , (, ), … , (, ) to the users C₁, C₂, T₁, … , T_N. Each target party T_i should introduce an auxiliary qutrit with the initial state . The initial state of the system reads

This scheme can be specified as the following steps.

Step 1 The users C₁, T₁, T₂, … , T_N’ s local operations.

Step 1.1 Taking c₁ as control qubit and c′ as the target qubit, user C₁ firstly applies a local CNOT gate U_CNOT (c^qubit; t^qubit) on qubits (c₁, c′ ) and then performs a Z-MB (measuring basis Z) on c′ . The measurement result is sent to T₁, T₂, … , T_i, … , T_N through N-way classical channels. If the result is | 1〉 _c′ /| 0〉 _c′ , they applied respectively a 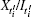gate on their individual qubit .

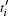
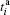
Step 1.2– Step 1.(N+ 1) The Step 1.2– 1.(N + 1) are essentially analogous. In the Setp 1.(i + 1), the user T_i first applies a local generalized CNOT gate U_GCNOT (c^qubit; t^qutrit) on his qubit and qutrit with qubit being the control. This generalized CNOT (GCNOT) gate U_GCNOT (c^qubit; t^qutrit) could be defined as

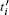
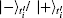
Then T_i performs a X-MB on qubit , and C₁ performs a Z_c1/I_c1 gate on qubit c₁ if T_i find . After these, the state (6) collapses to

Here, and in what follows, shows the Q-MB in which the particle x is measured.

Step 2 The users C₂, T₁, T₂, … , T_N’ s local operations.

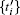
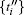
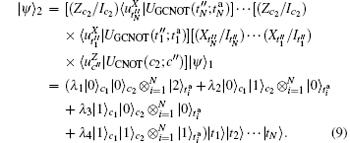
Step 2 is exactly the same as the one shown in Step 1. But c₁ to c₂, c′ to c″ , and to . After that, the state (8) will become

Step 3– Step (N + 2) The users C₁, C₂, T₁, T₂, … , T_N’ s local operations.

The last N steps are essentially analogous. In the (i + 2)th step, the user T_i applies firstly a local generalized controlled gate U_{GC− Vi} (c^qutrit; t^qubit), which applies a single-body gate V_i on the target qubit t^qubit whenever the control qutrit c^qutrit is | 1〉 , on qutrit and qubit t_i. Then, it is followed by performing a F-MB (measuring basis F^{[1, 28]}) on qutrit . The measurement result is sent to C₁ and C₂ through 2-way classical channels. Finally, C₁ and C₁ perform respectively an appropriate unitary transformation {I_cj/Z_k)_cj}, according to , on their individual qubits c₁ and c₂. It is shown that for k > 0 the operation Z_k is

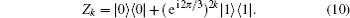
After these manipulations, the state (9) becomes

This completes the local implementation of the nonlocal N-target controlled-controlled gate. It consumes two shared (N + 1)-qubit GHZ states, N auxiliary qutrits, (3N + 2) local two-body gates, and 6N feed-forward corrections. Here the measurement in F-BM plays the same role as in quantum state teleportation: it provides the information needed to correct the nonlocal N-target controlled-controlled gate in the end, then this nonlocal gate works with unit fidelity and unit probability in principle.

This scheme has some advantages. First, it seems a significant reduction in the number of local two-body gate required for implementing this nonlocal (N + 2)-body gate via GHZ channel. We have showed that instead of 7N local two-body gates as required in Ref. [10], introducing N auxiliary qutrits and measuring respectively them in F-MB and using feed-forward corrections allows these to be reduced to (3N + 2) ones. An immediate benefit of this reduction is an equally significant speed-up in processing time. This will be useful as a testbed for more complicated quantum computing algorithms. Second, the auxiliary qutrits can be measured without destroying the coherence of the message qubits {c_j, t_i} and GHZ qubits {c′ , ; c″ , }. Third, at target nodes, each of GHZ qubits interacts with auxiliary qutrit only once, and each of interacts with homogeneously. This property would result in a simplified design for some QCC network schemes. If the GHZ qubits are photons and the auxiliary qutrits are atoms in cavities, for example, this means that each photon has to pass through the cavity only once. This will not require to store the photon in a buffer and then redirect it back to the cavity.^[28] Similarly, each auxiliary qutrit interacts with the target qubit t_i in the same way. Compared to Eisert’ s scheme, ^[10] however, the required physical resource has changed from 2N two-body Bell states to two N-body GHZ states plus N auxiliary qutrits. This may make the implementation of this new scheme more difficult in practice. The number of feed-forward corrections have also increased from 4N to 6N.

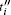
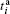
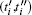
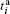
This scheme can be generalized to implement locally a nonlocal N-target and M control qubits gate by introducing N (M + 1)-dimensional qudits as catalysator. In this case, the number of local two-body gates required for this scheme is [(M + 1)N + M] and the shared entanglement is M (N + 1)-qubit GHZ states.

There are a few remarks concerning the proposed scheme. First, in some QCC network schemes, employing GHZ states as quantum channel can indeed save quantum resources and advance efficiency. This advantage can not be replaced by using Bell states Since the GHZ state is required to distribute, photons would be the best choice. The first entangled 3-photon GHZ state was experimentally realized in 1999.^[29] To date, a GHZ state up to 8-photon, which was created from four pairs of polarization-entangled photons, has been demonstrated.^[30] This 8-photon setup could serve a well-controlled few-qubit quantum simulation testbed for studying more efficient QCC network schemes. Recently, Gao and Yan et al.^[31] have presented a scheme for creating a N-photon GHZ state from a product state of N photons using weak nonlinearities. In this scheme, one can generate the desired multi-photon GHZ states directly instead of waiting for the supply of two-photon entangled states. Nevertheless, the distribution of entanglement over long distances, which is an indispensable process in many QCC schemes, has been a grand challenge in emerging quantum technologies. Several record-setting entanglement distribution experiments have already been reported, including entanglement distribution over 144 km in free space^[32] and over 300 km of fiber.^[33] Most recently, Pan et al. have reported an entanglement distribution over a two-link free space optical channel, where the entangled photon pairs are separated by more than 100 km.^[34] Besides being of fundamental interest, this result seems to be an effective way to solve the multi-photon entanglement distribution over a multi-link free space channel and represents a significant step towards a global quantum network. Second, the technique that we describe is independent of the particular quantum system used to encode quantum information. The only requirement is access to qutrits and the ability to realize a quantum interact between a qubit– qutrit system. It is known that most of the candidate systems for encoding quantum information naturally offer d-dimensional structures (d > 2, qudits). Coherent control over and between many of these dimensions has already been experimentally demonstrated and shown that qudit systems are better suited for certain QCC tasks.^{[12, 28, 35– 38]} Third, it seems that most of the local two-body gates required in our scheme should be applied on photons and matter systems jointly. Realizing a quantum interface between a photon and a stationary qubit has long been an outstanding goal in QCC. An example of implementing such an interface between dissimilar quantum systems is quantum teleportation.^{[39, 40]} In 2013, Gao et al. have experimentally demonstrated a quantum interface between a photonic qubit generated by a neutral quantum dot (QD) exciton and a semiconductor spin qubit generated by another QD.^[41] This shows that the two auspicious features of QDs can be combined to realize an elementary process of a QCC network where nodes incorporating a small number of stationary solid-state spin qubits are interconnected using photons. Some further interesting extensions include of a quantum interface between a photonic and a hole-spin, ^[41] and a interface between a qubit from the self-assembled QD and a qubit in a gate-defined QD, where coherent two-body gates have been demonstrated.^[42] The interface of photons and atomic ensembles would offer a fascinating playground for integrating the linear-optical and atomic-ensemble-based techniques for long-distance quantum communication and scalable optical quantum computation. Fourth, in addition to the GHZ states, the W states can also be used as quantum channel to implement locally the nonlocal N-target controlled– controlled gate probabilistically. The work is under study and we will publish elsewhere the study results. An attractive property of W channel is its entanglement being robust against state loss or white noise, ^[23] despite that the probability of successful implementation using W channel is always less than that of GHZ channel. Recently, eight-mode W-states have been experimentally demonstrated and precisely characterized.^{[25, 26]}

In conclusion, we have presented a scheme for implementing locally a nonlocal N-target controlled– controlled gate with unit fidelity and unit probability. We have showed that instead of 2N Bell states and 7N local two-body gates, as required for Eisert’ s scheme^[10] hiring two (N + 1)-qubit GHZ states as quantum channel and N auxiliary qutrits as catalyser allows the implementation of this nonlocal (N + 2)-body gate to be improved significantly. The design is built entirely of local single- and two-body gates, and only (3N + 2) two-body gates. This result shows that the computational complexity of the quantum network for doing the proposed implementation might be significantly reduced. This scheme can be generalized straightforwardly to a higher order nonlocal N-target and M control qubits gates by harnessing M (N + 1)-qubit GHZ states as quantum channel and N (M + 1)-dimension qudits as catalysator.