†Corresponding author. E-mail: xxlwlx@126.com
*Project supported by the National Natural Science Foundation of China (Grant No. 10574647), the Natural Science Foundation of Shandong Province, China (Grant No. Y2008A16), and the University Experimental Technology Foundation of Shandong Province of China (Grant No. S04W138).
We investigate how an optical squeezed chaotic field (SCF) evolves in an amplitude dissipation channel. We have used the integration within ordered product of operators technique to derive its evolution law. We also show that the density operator of SCF can be viewed as a generating field of the squeezed number state.
Quantum noise exists in every natural system.[1] Squeezed states exist where the noise in one of the chosen pair of observables is reduced below the vacuum or ground-state noise level, at the expense of increased noise in the other observable. Indeed, the squeezing effect improves both the interferometric and spectroscopic measurements. Therefore, in the context of interferometric detection and of gravitational waves, the squeezed state is very useful.[2] On the other hand, since every system is not absolutely isolated, dissipation or dephasing usually happens when a system is immersed in a thermal environment. A quantum state that passes through an amplitude damping channel is described by the master equation for density operator ρ [3, 4]
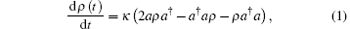
where κ is the rate of decay, a† and a are the creation operator and the annihilation operator, respectively, and [a, a† ] = 1. In this present work we investigate how an initial squeezed chaotic field (SCF), described by ρ 0 = (1 – ek) S† eka† aS, evolves in an amplitude dissipative channel (ADC), where (1 – ek) eka† a is the density operator of chaotic field, and
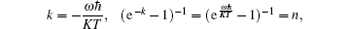
where K is the Boltzman constant, S(r) = exp[ir (QP + PQ)/2] is the single-mode squeezing operator, with [Q, P] = i, ħ = 1, and r is the squeezing parameter. Using the thermo entangled state representation, [5] we have neatly derived the solution to Eq. (1), which takes the infinitive operator-sum representation[6, 7]
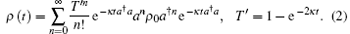
(Although this solution can also be deduced with the use of the superoperator method, these superoperators have no real representations.) Our task in this paper is to investigate how a SCF evolves in an amplitude dissipation channel, when an optical chaotic field gets squeezed in a cavity and later dissipates in an thermo-enviroment, we are also curious about how it evolves with time. At first glance, one might think that it would be easy to substitute ρ 0 = (1 – ek) S† eka† aS into Eq. (2) to obtain the result, actually, it is hard to do so, because the summation over n is impeded due to the existence of ρ 0 sandwiching between an and a† n. We shall employ the technique of integration (summation) within ordered product of operators[8] to overcome this obstacle and derive its evolution law. We also show that the density operator of SCF can be viewed as a generating field of the squeezed number state.
Before substituting ρ 0 = (1 – ek) S† eka† aS into Eq. (2) to make a summation, we should first convert ρ 0 into its normal ordering and then transform the result in anti-normal ordering so that the summation as Eq. (1) indicated can be proceeded, because the creation operator and the annihilation operators can be permuted within the anti-normal ordering. For this purpose, we write ρ 0 in the Fock representation
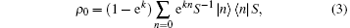
where 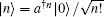
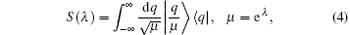
where | q〉 is the coordinate eigenstate
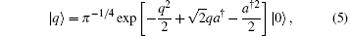
with the overlap
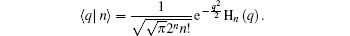
Here, Hn(q) is the Hermite polynomial, thus
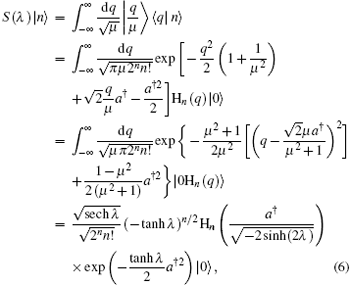
where in the last step we have used the integration formula
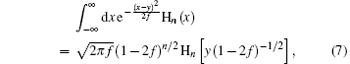
or we have
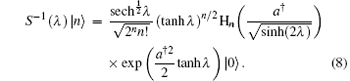
Therefore, a squeezed number state can be considered as an Hermite excitation on the squeezed vacuum state.
By substituting Eq. (8) into Eq. (3) and using
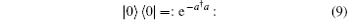
as well as the generating formula of the Hermite polynomials
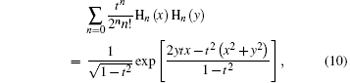
we have
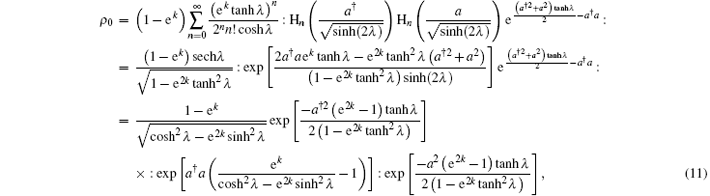
which is the normally ordered expansion of the squeezed chaotic field.
Due to k = – ω ħ /KT,

and
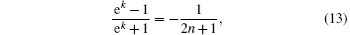
we let
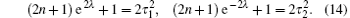
It follows that
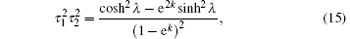
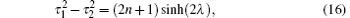
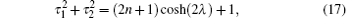
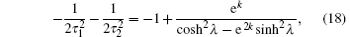
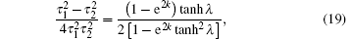
thus
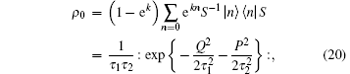
where

the density operator of the SCF is a normally ordered bivatriate distribution operator in phase space. One can check the completeness that

Further, let
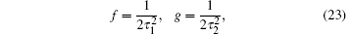
then
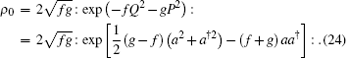
Next, we derive the anti-normal ordering form of ρ 0 by using[10]
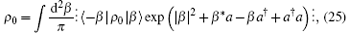
where ⁝ ⁝ stands for the anti-normal ordering and | β 〉 is a coherent state
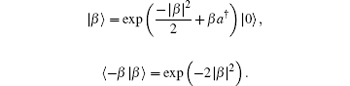
By substituting Eq. (20) into Eq. (25) and using the integral formula[10, 11]
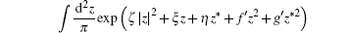

whose convergent condition is
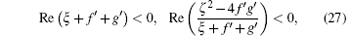
or

we have the anti-normal ordering form of ρ 0
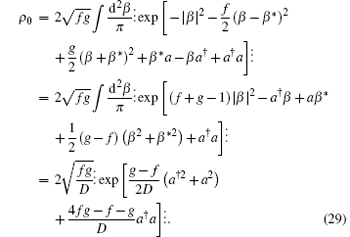
We note that the operator formula
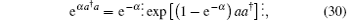
so
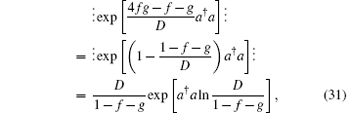
and equation (29) becomes
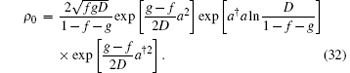
By substituting Eq. (32) into Eq. (2) and using
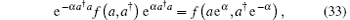
equation (32) becomes
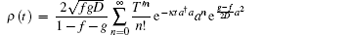
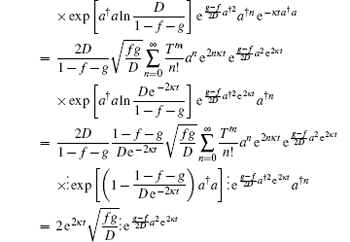
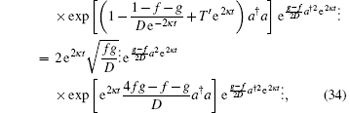
which is the antinormally ordered form of ρ (t).
Using the P-representation theory in the coherent state basis and 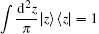
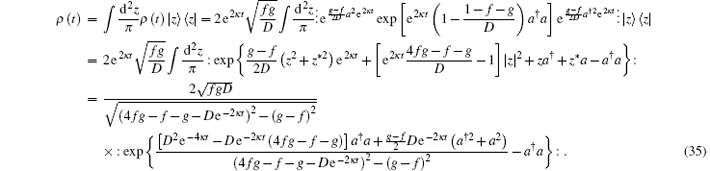
We can check that when t = 0, e− 2κ t = 1, due to

then,

as expected.
By comparing Eq. (35) with Eq. (24) we can see clearly the evolution law of a SCF in an amplitude damping channel.
In summary, we have investigated how a SCF evolves in an amplitude dissipation channel. By using the integration within ordered product method, [12– 16] we derived its evolution law. We also show that the density operator of the SCF can be viewed as a generating field of the squeezed number state.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|


