Quantum teleportation by employing classical communication and the shared resource of entanglement allows one to transmit an unknown quantum state from a sender to a receiver that are spatially separated. The first teleportation protocol was proposed by Bennett et al. using the Einstein– Podolsky– Rosen pair.^[1] Then the three-qubit GHZ state and a class of W states were revealed to be the ideal resource for faithful teleportation of the one-qubit state.^{[2, 3]} For the two-qubit state teleportation, the tensor product of two Bell states^[4] and the genuine four-qubit entangled state^[5] are shown to have the ability of faithful teleportation. For the three-qubit state, teleportation has been investigated in Refs.  [6] and [7] in terms of a genuine entangled six-qubit state. And some entangled 2n-qubit states have been presented for the n-qubit state teleportation.^{[8– 10]}

How can we know if a general quantum state is the ideal resource for faithful teleportation, or if it is useful for teleportation with fidelity better than that of the classical states? For the bipartite case, it has been shown that the quantum states which are not useful for quantum teleportation compose a compact convex set, and a teleportation witness has been presented for the first time in Ref.  [11]. A complete set of teleportation witnesses to detect all the ideal resources for teleportation was constructed in Ref.  [12] and a systematic method to construct a teleportation witness from an entanglement witness was provided in Ref.  [13]. The properties of a teleportation witness were further studied in Ref.  [14]. For the multipartite case, the necessary and sufficient condition that the genuine 2n-qubit entanglement channels must satisfy for teleporting an arbitrary n-qubit state was provided in Ref.  [15], and the criterion of multiqubit states for n-qubit teleportation was studied in Refs.  [16] and [17].

In this paper, we first study multiqubit teleportation and propose a linear operator to detect the ideal resource for multiqubit teleportation. The operator is expressed in terms of the local complementary observables. It gives a sufficient condition for the detection of all ideal resources for multiqubit teleportation. The operator can also be used to detect multiqubit entanglement and serves as a necessary condition for full separability. We also analyze the teleportation witness for the bipartite high-dimensional case. Moreover, the remaining problem from Ref.  [13] is solved by explaining the optimality of the teleportation witness.

We first consider n-qubit systems. Let a₁, a₂, and a₃ be three-dimensional unit vectors. Three observables X_k = a_k · σ (k = 1, 2, 3) are complementary if they satisfy X₁X₂X₃ = − iI₂, where , I₂ is the 2 × 2 identity matrix, and σ = (σ ₁, σ ₂, σ ₃), σ ₁ = | 0〉 〈 1| + | 1〉 〈 0| , σ ₂ = i(| 0〉 〈 1| – | 1〉 〈 0| ), σ ₃ = | 0〉 〈 0| – | 1〉 〈 1| are the Pauli matrices; this means that the orientation of the basis formed by three real vectors is right-handed, with the same orientation as that of the three Pauli matrices. Let , i = 1, … , n, be complementary observables acting on A_i. We define the operator

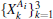
The operator Γ can be used to detect the ideal resources for n-qubit teleportation.

Theorem 1 Any 2n-qubit pure state ρ = | ϕ 〉 _{A1 … An, B1 … Bn}〈 ϕ | , with qubits A_i in the A part and qubits B_i in the B part, can be used to faithfully teleport an arbitrary n-qubit state if there exist complementary observables 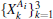acting on A_i such that 〈 Γ 〉 _ρ = 1.

Proof First, as is well known, the tensor product of Bell states

is an ideal resource for multiqubit teleportation. Let us expand | ϕ ⁺ 〉 _{A1 … An, B1 … Bn}〈 ϕ ⁺ | in terms of the Pauli operators. Note that the expectation values of σ _k with respect to | ϕ ⁺ 〉 _{A1 … An, B1 … Bn}〈 ϕ ⁺ | are all zero except for the case in which there are even numbers of σ _k’ s, with one half acting on some qubits of the A part and the other half acting on the corresponding qubits of the B part, namely,

For the case with different Pauli operators acting on the same t-th qubit in A and B parts, if σ _k acts on qubit A_t and σ _k′ acts on qubit B_t, then

due to ∑ _it, _{jt = 0, 1} 〈 i_t| σ _k| j_t〉 〈 i_t| σ _k′ | j_t〉 = 0 for k ≠ k′ , k, k′ = 0, 1, 2, 3, where σ ₀ is the identity operator. From the above analysis, we have

Denote . Then are complementary observables satisfying , i = 1, 2, … , n. The unitary operators and the complementary observables can be mutually determined uniquely. If 〈 Γ 〉 _ρ = 1 for some local complementary observables, then there exist unitary operators U^A₁, … , U^A_n such that

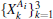
is of form (2). Therefore, ρ is local unitarily equivalent to | ϕ ⁺ 〉 _{A1 … An, B1 … Bn}〈 ϕ ⁺ | and is an ideal resource for multiqubit teleportation.

Theorem  1 provides a method to detect the ideal resource for multiqubit teleportation. All quantum states | ϕ 〉 _{A1 … An, B1 … Bn} that can be detected by Theorem  1 are local unitarily equivalent to | ϕ ⁺ 〉 _{A1 … An, B1 … Bn}. And if a quantum state is local unitarily equivalent to | ϕ ⁺ 〉 _{A1 … An, B1 … Bn}, then it must satisfy 〈 Γ 〉 _ρ = 1 for some local complementary observables 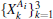, since U^A₁ ⊗ … ⊗ U^A_n ⊗ U^B₁ ⊗ … ⊗ U^B_n| ϕ ⁺ 〉 = U^A₁ (U^B₁)^T ⊗ … ⊗ U^A_n (U^B_n)^T| ϕ ⁺ 〉 in the calculation of the mean values of the observables. Although Theorem  1 only gives a sufficient condition for the detection of the multiqubit teleportation resource, it is experimentally feasible. Moreover, one only needs to measure different local complementary observables on the A part, the observables on the B part are fixed. For example, to detect | ϕ ⁺ 〉 _{A1 … An, B1 … Bn}, one simply chooses X_k = σ _k, k = 1, 2, 3. Theorem  1 may also help in the characterization of the teleportation witness in multiqubit systems.

Corollary 1 If a 2n-qubit mixed state ρ is fully separable, then 〈 Γ 〉 _ρ ≤ 1/2ⁿ for all complementary observables 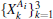acting on qubit A_i, i = 1, … , n.

Proof Due to the linearity of the operator Γ , we only need to prove 〈 Γ 〉 _ρ ≤ 1/2ⁿ for all pure fully separable states | ψ 〉 . By proving 〈 | ϕ ⁺ 〉 _{A1 … An, B1 … Bn}〈 ϕ ⁺ | 〉 _{| ψ 〉 〈 ψ |} ≤ 1/2ⁿ, one can prove the corollary directly.

Corollary  1 gives a necessary condition for the fully separable state. It shows that if the expectation value of Γ is larger than 1/2ⁿ for some complementary observables, then the quantum state is entangled.

Now we consider the detection of the ideal resource for the teleportation of high-dimensional systems. Let H_n be an n-dimensional complex vector space, with 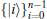an orthonormal basis. Let ρ be a density matrix in H_n ⊗ H_n. The optimal fidelity of teleportation with ρ as the entangled resource is given by^{[18– 20]}

Here F(ρ ) is the fully entangled fraction with respect to ρ

where U is any n × n unitary matrix, I_n is the n × n identity matrix, and | ψ ⁺ 〉 is the maximally entangled state

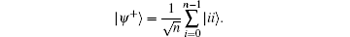
A state ρ is a useful resource for teleportation if and only if F(ρ ) > 1/n.^[19] If F(ρ ) ≤ 1/n, the fidelity (3) is no better than the separable states. Recently in Ref.  [11], the authors showed that the set of states which are not useful for quantum teleportation, i.e., their fully entangled fractions are no more than 1/n, is also convex and compact. Therefore there exist witness operators which can detect some entangled states that are useful for teleportation.

A teleportation witness W is a Hermitian operator satisfying: (i) Tr(Wρ ) ≥ 0 for all states ρ that are not useful for quantum teleportation, (ii) there exists at least one entangled state ρ which is useful for teleportation such that Tr(Wρ ) < 0.^{[11, 13]} For entangled state ρ , if Tr(Wρ ) < 0, then teleportation witness W can detect ρ as a useful resource for teleportation. Between two teleportation witnesses W₁ and W₂, W₁ is considered to be better if W₁ can detect all the entangled states that can be detected by W₂. A witness is said to be optimal if there exist no better witnesses.^[21] It is obvious that any teleportation witness is also an entanglement witness.

Since all separable states are positive under partial transpositions (PPT) and there exist PPT entangled states, the set of all separable states is a proper subset of the set of PPT states. Similarly, since all PPT states are not useful for teleportation^[19] and there exist nonpositive partial transposition (NPT) entangled states that are also not useful for teleportation, ^[22] the set of PPT states is again a proper subset of the set of states that are not useful for teleportation. A teleportation witness is a hyperplane that separates a point, which is an entangled state that is useful for quantum teleportation, from the convex and compact set of states that are not useful for teleportation. An optimal teleportation witness is then a hyperplane that is tangent to the set of states which are not useful for teleportation (see Fig.  1).

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Geometric characterization of a teleportation witness.

Now we consider the teleportation witness

The W(I) is a teleportation witness in the sense that for arbitrary states ρ which are not useful for quantum teleportation, i.e, F(ρ ) ≤ 1/n, Tr(W(I)ρ ) ≥ 0. And Tr(W(I)| ψ ⁺ 〉 〈 ψ ⁺ | ) < 0 for the ideal teleportation resource | ψ ⁺ 〉 〈 ψ ⁺ | . Furthermore, W(I) is an optimal teleportation witness. Consider the following product vectors:

where j, k, l = 0, 1, … , n – 1 and k < l. These d² product vectors are linear independent and satisfy Tr(W(I)K_j) = 0, Tr(W(I)K_kl) = 0, . Note that if a set of product vectors P_W = {| e, f〉 : Tr(W| e, f〉 〈 e, f| ) = 0} spans the relevant product vector space, then W is an optimal entanglement witness.^[21] Since an optimal entanglement witness is surely an optimal teleportation witness, W(I) is an optimal teleportation witness. In Ref.  [13], a teleportation witness for the bipartite system is given and its optimality is proved for the two-dimensional case, while that for the high-dimensional case is left. We find that W(I) is exactly the teleportation witness in Ref.  [13]. Then the problem proposed in Ref.  [13] is solved by proving the optimality of the teleportation witness W(I).

In fact, teleportation witness W(I) is an entanglement witness of the form W = α I – | ψ 〉 〈 ψ | with α = max_{| ϕ 〉 = | a〉 ⊗ | b〉} | 〈 ψ | ϕ 〉 | ², where | ψ 〉 is an entangled pure state. Entanglement witness W can detect the entanglement of | ψ 〉 and that of NPT states. The distance between entangled state | ψ 〉 and the set of separable states is α . In particular, the distance between the maximally entangled state | ψ ⁺ 〉 and the set of separable states is 1/n. The distance between | ψ ⁺ 〉 and the set of PPT states is also 1/n.

Now we define the teleportation witness

One can verify that W(U) is an optimal teleportation witness for arbitrary unitary operator U. Furthermore, the set of teleportation witnesses {W(U)} is complete, since for arbitrary entangled state ρ that is useful for teleportation, there exists a unitary operator U such that Tr(W(U)ρ ) < 0.

We have presented an experimental approach to detect the ideal resource for quantum teleportation in multiqubit systems by deriving a condition to detect the local unitary equivalence of the tensor product of Bell states. Our criterion only involves local measurements on the complementary observables in half of a system. It also helps to characterize the teleportation witness for multiqubit systems.^[14] For bipartite high-dimensional systems, we have analyzed the teleportation witnesses. Moreover, we have solved the open problem presented in Ref.  [13].