†Corresponding author. E-mail: flyan@hebtu.edu.cn
‡Corresponding author. E-mail: gaoting@hebtu.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 11475054 and 11371005), Hebei Natural Science Foundation of China (Grant Nos. A2012205013 and A2014205060), the Fundamental Research Funds for the Central Universities of Ministry of Education of China (Grant Nos. 3142014068 and 3142014125), and Langfang Key Technology Research and Development Program of China (Grant No. 2014011002).
We directly introduce a Bell-type inequality for four-qubit systems. Using the inequality we investigate quantum nonlocality of a generic family of states | G abcd〉 [ Phys. Rev. A65 052112 (2002)] and several canonical four-qubit entangled states. It has been demonstrated that the inequality is maximally violated by the so called “four-qubit the maximally entangled state | Gm〉” and it is also violated by four-qubit W state and a special family of states | G ab00〉. Moreover, a useful entanglement-nonlocality relationship for the family of states | G ab00〉 is derived. Finally, we present a scheme of preparation of the state | Gm〉 with linear optics and cross-Kerr nonlinearities.
Entanglement is an inherent consequence of multipartite quantum systems and as a physical resource, quantum entanglement has many important applications in quantum computation and quantum information.[1] It is worth noting that a fundamental question in the theory of entanglement is how to characterize and quantify entanglement.[2– 9] In recent years, the characterization for multipartite entangled states has been considerably developed. The classification of a bipartite system under local unitary operators can be carried out by singular value decomposition.[1] Under stochastic local operations and classical communication (SLOCC), a three-qubit entangled pure state can be converted either to the GHZ-state or to the W-state.[10, 11] In the case of a four-qubit entangled pure state, it has been shown[12] that there are nine classes of states. Recently, for the pure multipartite entangled states, Liu et al.[13] proposed a method for local unitary classification using the symmetry and tensor decomposition. For quantification of the entanglement, as is well-known, one can take the concurrence[14] as a measure of bipartite entanglement. In 2000, Coffman et al.[15] proposed the three-tangle which is a measure of genuine tripartite entanglement. Next the expressions of four-tangle[16– 18] and n-tangle[19, 20] have been derived.
Quantum theory allows correlations between spatially separated systems, while local hidden variable (LHV) theory gives an upper bound that quantifies the degree of nonlocality for a given inequality. A famous inequality as a way of verifying predictions of quantum mechanics versus those of all possible LHV theories was first proposed by Bell.[21] In 1969, Clauser et al. derived another correlation inequality, the Clauser– Horne– Shimony– Holt (CHSH) inequality, [22] which also provides a way of experimentally testing LHV theory as an independent hypothesis separated from the quantum formalism. It has been proved that[23, 24] for the standard projective measurements all pure entangled states of two qubits violate the correlation CHSH inequality. In the case of three parties, Ací n et al.[25] considered a Bell inequality and showed that all three-partite pure entangled states violate it. For the N-qubit case, the best-known inequality is the Mermin– Ardehali– Belinskiĭ – Klyshko (MABK) inequality, [26– 28] which is included in the Werner– Wolf– Ż ukowski– Brukner (WWZB) inequality[29, 30] as a special case. It has been proved that quantum violation of this inequality increases with the number of particles. Several Bell-type inequalities have been established by using an algebraical method, [31– 33] and by finding out the stabilizer group of quantum states.[34, 35] By determining facets of the correction polytope, Pitowsky et al.[36] and Wu et al.[37] obtained the new Bell inequalities.
In this paper, we discuss mainly the nonlocality for several canonical four-partite entangled states. In the Hilbert space ℂ 2)⊗ 4, a general four-qubit pure state may be written as

where aijkl are the complex coefficients with the basis vectors | ijkl〉 , and A, B, C, and D are the locations of qubits, respectively. In nine classes of four-qubit entangled pure states, [12] we here consider the generic family
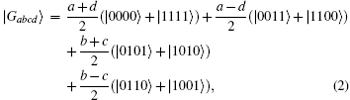
where the complex parameters a, b, c, and d satisfy the normalization condition | a| 2 + | b| 2 + | c| 2 + | d| 2 = 1. For the sake of simplicity throughout this paper we concern ourselves only with the cases where all a, b, c, and d are real. Obviously, the generic family contains four-qubit GHZ state 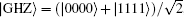
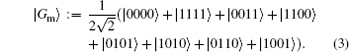
We note that these states do not violate the previous four-qubit Bell inequalities[34, 35] with the specified experimental settings. Next we introduce a Bell-type inequality that shows different degrees of violation when evaluated for different entangled states. In particular, the maximal violation is obtained with the four-qubit maximally entangled state | Gm〉 . At last, we present a scheme for preparing the state | Gm〉 with linear optics and cross-Kerr nonlinearities.
Firstly, we consider the four-qubit maximally entangled state | Gm〉 . Quantum mechanically, there are 16 operators {Si, i = 1, … , 16} satisfying the eigenvalue equations Si| Gm〉 = ± | Gm〉 , namely, σ 0σ 0σ 0σ 0, σ xσ xσ xσ x, σ yσ yσ yσ y, σ zσ zσ zσ z, σ xσ xσ 0σ 0, σ xσ 0σ xσ 0, σ 0σ xσ xσ 0, σ xσ 0σ 0σ x, σ 0σ xσ 0σ x, σ 0σ 0σ xσ x, σ yσ yσ zσ z, σ yσ zσ yσ z, σ zσ yσ yσ z, σ yσ zσ zσ y, σ zσ yσ zσ y, and σ zσ zσ yσ y, where σ 0 is the identity operator and σ i (i = x, y, z) is Pauli operators. From the above 16 operators, we choose four operators and combine them as
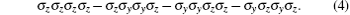
Whereupon, we can derive the expectation value of the above operator for the four-qubit maximally entangled state | Gm〉 , that is,
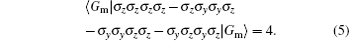
Based on the assumption of local realism, where all four qubits are locally but realistically correlated, we can introduce a linear Bell-type inequality. Suppose that every observer is allowed to choose between two dichotomic observables. More precisely, there is an ensemble of four spatially separated qubits and the measurements 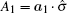
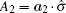
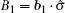
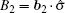
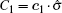
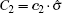
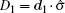
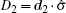
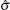
Define the Bell-type operator
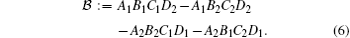
Clearly, under the experimental setting
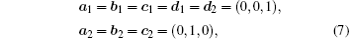
the present Bell-type operator is equal to the expression (4).
Suppose that p(a1, a2, b1, b2, c1, c2, d1, d2) is the probability that, before the measurements are performed, the system is in a state, where A1 = a1, A2 = a2, B1 = b1, B2 = b2, C1 = c1, C2 = c2, D1 = d1, and D2 = d2. Let correlation function 〈 𝓑 〉 denote the average over many runs of the experiment. We then have
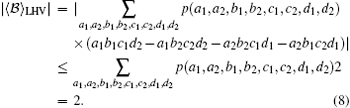
In addition,

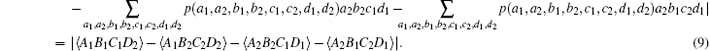
Combining inequality (8) and Eq. (9), we obtain Bell-type inequality
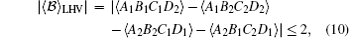
which holds for LHV theories. It should be pointed out that one can obtain the above Bell inequality by using Wu’ s method.[37] As a matter of fact, LHV models can be associated with correlation polytope, whose facets define Bell inequalities. It is easy to prove that 𝓑 /2 = 1 is a facet of polytope for a four-qubit system.
We next study the quantum nonlocality of the generic family | Gabcd〉 using the above operator 𝓑 in the special setting stated by Eq. (7). It turns out that
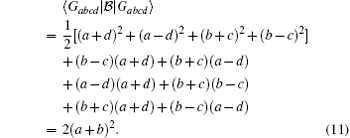
Under the constraint condition, a2 + b2 ≤ 1, we plot in Fig. 1 the quantum prediction 〈 Gabcd| 𝓑 | Gabcd〉 versus a and b. Obviously, the numerical value of the violation of the inequality depends on a and b.
In particular, for the four-qubit maximally entangled state | Gm〉 , based on Eq. (5) one can conclude that this is indeed a violation of the inequality (10) where the LHV bound is 2. Under the optimal setting given above, the maximal violation of the Bell-inequality reaches its maximum value of 4 for the four-qubit maximally entangled state | Gm〉 . The inequality is therefore, in a sense, optimal. This is also the reason why we call | Gm〉 the maximally entangled state.
A remarkable feature of the present inequality is that there exists a family of the four-qubit entangled states where all states violate it. The family reads
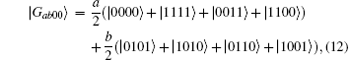
where a and b satisfy ab > 0 and a2 + b2 = 1. Consider genuine four-tangle τ (4, 8), [17, 18] which is regarded as a measure of four-qubit entanglement and constructed by means of a four-qubit invariant of degree 8 expressed in terms of three-qubit invariants, we have
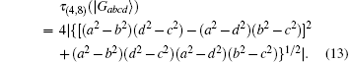
Then, for the state | Gab00〉 , four-tangle is τ (4, 8) = 4a2b2. In the light of the result in Eq. (11) we obtain a useful relationship between four-partite entanglement (four-tangle) and nonlocality for the family of the four-qubit entangled states | Gab00〉
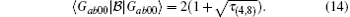
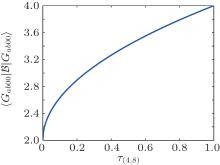
Figure 2 shows the quantum nonlocality versus four-tangle for states | Gab00〉 . It has been shown that quantum violation varies with four-tangle τ (4, 8) and when τ (4, 8) = 1 (i.e., 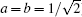
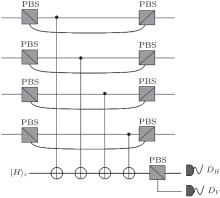
We now discuss a possible experimental realization of the maximally entangled state | Gm〉 with linear optics and cross-Kerr nonlinearities.[38, 39] The setup for creating the desired state is shown in Fig. 3. Initial state is fed by 
Finally, let us discuss several specific examples for the candidates of four-qubit maximally entangled state using the introduced Bell-type inequality. Under the specified experimental setting, we calculate expectation values of operator 𝓑 for four-qubit GHZ state, cluster state, W state, two-EPR-pair state,
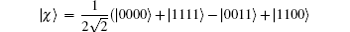
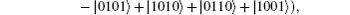
presented by Yeo and Chua, [40]
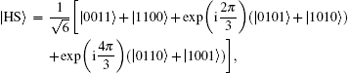
introduced by Higuchi and Sudbery, [41] and
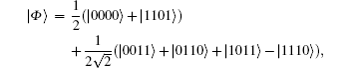
investigated by Brown et al.[42] The result is that the inequality is not violated by these states except the W state, | 〈 W| 𝓑 | W〉 | = 2.5. Hence, the present inequality can act as a strong entanglement witness for the entangled state | Gm〉 .
In summary, we have introduced a four-qubit Bell-type inequality with the method of the stabilizer group of quantum states. Under the given experimental setting, the inequality is maximally violated by the four-qubit maximally entangled state | Gm〉 which does not violate previous four-qubit Bell-type inequality.[34, 35] We have studied the quantum nonlocality of the generic family | Gabcd〉 and several four-qubit states using the inequality and shown that the inequality is also violated by the four-qubit W state and a family of four-qubit entangled states | Gab00〉 . Also, we have derived a useful relationship between four-partite entanglement and nonlocality for the family of four-qubit entangled states | Gab00〉 . Therefore, the results derived from the inequality indicate that it can act as a strong entanglement witness for the family | Gab00〉 , especially for | Gm〉 . Experimentally, we notice that the present inequality is easier to evaluate because it contains only four terms. In addition, we have proposed a scheme of experimental realization of the state | Gm〉 with linear optics and cross-Kerr nonlinearities. It is straightforward to show in principle that the desired state can be prepared after a simple single-photon detection and post-selection. Finally, it is worth noting that the discovery of the entanglement-nonlocality relationship, as well as the results reported in Refs. [43]– [46] will greatly facilitate the development of entanglement and their application in quantum information processing.[47– 52]
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|
| 38 |
|
| 39 |
|
| 40 |
|
| 41 |
|
| 42 |
|
| 43 |
|
| 44 |
|
| 45 |
|
| 46 |
|
| 47 |
|
| 48 |
|
| 49 |
|
| 50 |
|
| 51 |
|
| 52 |
|