†Corresponding author. E-mail: fye@iphy.ac.cn
*
We investigate how an externally imposed curvature influences lipid segregation on two-phase-coexistent membranes. We show that the bending-modulus contrast of the two phases and the curvature act together to yield a reduced effective line tension. On largely curved membranes, a state of multiple domains (or rafts) forms due to a mechanism analogous to that causing magnetic-vortex formation in type-II superconductors. We determine the criterion for such a multi-domain state to occur; we then calculate respectively the size of the domains formed on cylindrically and spherically curved membranes.
Lipid membranes play important roles in maintaining cell integrity and intracellular trafficking.[1, 2] At high temperatures, the three main components of the membranes (saturated lipids, unsaturated phospholipids, and cholesterols) form a homogeneous mixture; below a critical demixing temperature, the three components segregate into two coexistent fluid phases, a saturated-lipid-enriched liquid-ordered (Lo) phase and unsaturated-phospholipid-enriched liquid-disordered (Ld) phase. Small Lo domains formed on cell membranes are also referred to as rafts.[3] The Lo phase (or rafts) has a larger bending modulus than the Ld phase.[4– 6] There have been a large body of studies[7– 18] investigating how membrane curvature influences the segregation of membrane lipids. All these studies are based on a physical mechanism that the Lo phase because of its larger resistance to bending prefers flatter regions and drives the Ld phase to more curved regions, i.e., these studies have implicitly assumed what matters is the variation of curvature rather than the curvature itself.
In this letter, we investigate how a uniform externally imposed curvature may influence lipid segregation on an Lo– Ld coexistent membrane. We show that, with the presence of a bending-modulus contrast, the curvature of the membrane induces the lipids to tilt away from the membrane normal and yields a reduced effective line tension between the lipid domains; when the curvature is larger than a certain critical value, lipid segregation leads to the formation of multiple Lo/Ld domains (or rafts) of a microscopic lengthscale rather than a complete separation of the two phases. We determine the criterion for the multi-domain pattern to occur; we then calculate respectively the size of the domains formed on cylindrically curved and spherically curved lipid membranes. We point out that although inspired by lipid systems the results obtained in this letter apply to any membranes that contain two distinct smectic phases.
Nonzero curvatures of lipid membranes can be either induced by their intrinsic spontaneous curvatures or imposed externally. We consider the latter case. (More precisely, we are interested in membranes whose curvatures are different from their spontateous values, including flat membranes with nonzero spontaneous curvatures (SC). Although this paper focuses on membranes having zero SC, the results achieved here can be easily generalized (with suitable modifications) to those with nonzero SC. In particular, when applied to flat membranes with nonzero SC, our results explain why the size of in vivo rafts is only a few nanometers.) Examples of lipid membranes with an externally imposed curvature includes in vivo membranes attached to BAR domains of proteins[19] and in vitro membranes attached to rigid substrates. There are two possible extreme types of lipid configurations resulting from an imposed curvature: (i) the lipids are perpendicular to the membrane surface and the energy cost originates from the splay energy cost of lipid orientation; and (ii) the lipids are parallel to each other, and the energy penalty is induced by the deviation of lipids’ orientations from the membrane normals, or more microscopically, by the relative sliding of the lipids with respect to one another.
In general, the lipid configuration of a curved membrane should be a superposition of the aforementioned two types. The corresponding elastic energy density thus includes two parts, the splay energy and the tilt energy penalty,

where n and N are unit vectors representing, respectively, lipid orientation and membrane normal, ∇ ′ represents the two-dimensional derivative on a curved surface, [20]K is the splay coefficient, and C is a coefficient measuring how strongly n is locked to N. The combination of K and C gives a characteristic length 
For an Lo– Ld coexistent membrane, the total energy includes the contributions from both phases. We will use subscripts “ o” and “ d” to distinguish the quantities of these two phases. For convenience in the expressions, we will also use the subscript i, with i = 1 representing the phase with smaller volume fraction and i = 2 representing the one with larger volume fraction; in a case of no ambiguity, we will use a symbol without subscript to represent the corresponding quantities of both phases. The total energy of a two-phase-coexistent membrane should also include a phase-boundary energy cost, which equals the product of the line tension t and the phase-boundary length. To minimize the boundary energy, the two phases on a flat membrane completely separate from each other, with each phase forming a large single domain. However, for a curved membrane, such a single domain may become unstable and split into multiple domains.
We now present the reason for the splitting of large single domains and determine the corresponding instability criterion. As illustrated in Fig. 1, when subjected to an externally imposed curvature, the Lo lipids tilt away from the membrane normals and become more parallel to each other so as to reduce the splay energy cost, given that Ko is larger than Kd. The anchoring energy, i.e., the second term in Eq. (1), constraints the tilting to occur within a narrow region of size ∼ ξ around the phase boundary. The energy change induced by such tilting can be computed. To simplify calculation, we assume that the size of the large single domains resulting from a complete phase separation is much larger than ξ and that the imposed curvature is much smaller than 1/ξ . Thus, in the aforementioned phase-boundary region, the splay ∇ ′ · ni can be approximated by 2H + (− )i∂ γ i/∂ si, where H is the mean curvature, si is the distance between the phase boundary and the lipid location in phase i (i.e., the arc length of the geodesic perpendicular to the phase-boundary line), and γ i is the angle between the membrane normal and the orientation of lipids of phase i. Note that the lipids now tilt in the plane defined by the membrane normal and the tangential vectors of these geodesics. The factor (− )i is added into the expression of ∇ ′ · ni because of the opposite directionality of s1 and s2. Substituting the approximate expression of ∇ ′ · ni into Eq. (1) and taking the functional derivative yields γ i = γ bexp(− si/ξ i), where γ b represents the deviation angle at the phase boundary. The energy change resulting from the lipid tilting can then be obtained by minimizing over γ b the sum of the energies of Lo and Ld. The combination of this energy change and the line tension t produces a reduced effective line tension:

Equation (2) clearly shows te can be lowered either by increasing H or the contrast between Ko and Kd or by decreasing Co and Cd.
The instability criterion of the single-domain state can then accordingly be obtained by simply setting te = 0. We can further simplify this criterion to an approximate form: t/H2 ≲ Kξ . Given that K is of order 10− 19 J for most lipid systems[20] and ξ can be assumed to be comparable to the membrane thickness and is thus of order 1 nm, [21, 22] the criterion is then t/H2 ≲ 10− 28 J· m. Depending on the compositions and temperature, the line tension t on a lipid membrane usually varies between 1 pN and 0.01 pN (or even smaller).[5, 6, 23, 24] For t ∼ 1 pN, the critical curvature Hc is thus of order 108 m− 1; for t ∼ 0.01 pN (for example, in systems with the presence of hybrid lipids, [25]) Hc is of order 107 m− 1.
As te becomes negative, the large single domains resulting from a complete phase separation become unstable and split into multiple small domains. In the following paragraphs, we calculate the size of the lipid domains formed on cylindrically curved and spherically curved membranes, respectively.
For a lipid membrane subjected to a uniform cylindrical curvature, we assume there is translational symmetry along ez, the direction of the long axis of the cylinder, and that the lipids align perpendicular to ez. In this case, a domain is a strip along ez, and the three-dimensional problem becomes a two-dimensional problem. The splay of the lipid orientation can then be expressed as ∇ ′ · ni = cosγ i[1 + ∂ γ i/∂ θ i]/Rc, where Rc is the radius of the cylinder and the θ ’ s are the azimuthal angles representing the lipid location in a domain. In the center of a domain, i.e., at θ i = 0, the lipids align along the membrane normal with γ i = 0. Substituting the expression of ∇ ′ · ni into Eq. (1) and then differentiating the energy density with respect to γ i yields γ i = Aisinh(θ iRc/ξ i), where the A’ s are the amplitudes and the approximations ξ i ≪ Rc and γ i ≪ 1 have been used. Approximately speaking, the deviation γ i decays exponentially for domains of size much larger than ξ i and linearly for those of a size smaller than ξ i. The amplitudes A1 and A2 are not independent from each other — they are related by the continuity condition 

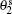

which clearly shows a competition between the energy penalty of the line tension and the energy gain of the director tilting induced by the difference between K1 and K2. The critical line tension tc, below which the completely separated state becomes unstable, is given by the maximum value of the second term in the parenthesis in Eq. (3), which is the same as the one we can obtain from Eq. (2) by setting te = 0 and H = 1/(2Rc).
At t < tc, a stable multi-domain ground state is expected. The domain size can be determined by numerically minimizing Eq. (3) over 

In addition to the numerical results, we also present in the following analytical results for the small t limit so as to clearly elucidate the dependence of the domain size 



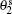

where 




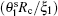



which is inversely proportional to | r − 1| and independent of the radius Rc (the linear domain size is thus linearly proportional to Rc). In addition, the angular size is now more sensitive to the variation of t than the angular size given in Eq. (4) is.
We proceed to address lipid segregation on a spherically curved membrane. A complete phase separation now leads to the formation of a single (curved) disk of L1 lipids embedded in an L2-lipid sea. The instability criterion of the single-disk pattern can be obtained from Eq. (2) by setting te = 0 and H = 1/Rs. For a negative te, a multi-domain pattern forms. In the case of ϕ ∼ 1/2, the shape of the formed multiple domains is complicated, and this complication makes an analytic calculation of the system energy inaccessible. We will study the ϕ ∼ 1/2 case in a numerical approach in a future publication and consider here only the case of ϕ ≪ 1/2. In this case, we have a pattern of multiple L1 disks embedded in an L2 sea.
We first give the explicit form of the energy as a function of the deviation angle γ and the equation determining how γ varies from the center of a domain to the domain edge. We adopt a spherical-coordinate description for the positions of the lipids, with the point of zero polar angle (i.e., θ = 0) corresponding to the center of an L1 domain, and we assume γ only depends on the polar angle θ but not the azimuth angle. Thus, for the total energy, we have


where Rs is the radius of the sphere, 


We now proceed to determine the domain size, i.e., the size of the L1 disks. Given the constraint ϕ ≪ 1/2, the distance between the disks becomes much larger than the disk size; and, in the L2 sea, only a narrow annulus around the disks contributes to the system energy. Furthermore, because the domain size is small, the deviation angle is nonzero only at small θ ’ s. We thus replace cotθ and cscθ in Eq. (7) by 1/θ , and obtain γ 1 ∝ BI1(b1θ ) and γ 2 ∝ BK1(b2θ ), where 
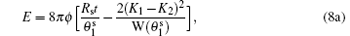 |
 |
Minimizing this energy yields the domain size. Figure 2(e) shows the numerical results, which are qualitatively similar to the results of cylindrically curved membranes with small ϕ [see Fig. 2(d)].
We conclude with a remark that the multi-domain-inducing mechanism addressed in this paper is different from that using elastic repulsions to stabilize multiple domains on a lipid vesicle, [5, 26], but analogous to the mechanism via which a large magnetic field induces the formation of magnetic vortices in type-II superconductors.[27] The tilt penetration length ξ in this work is the counterpart of the magnetic field penetration length in superconductors. What corresponds to the superconducting coherence length is the correlation length of the density fluctuation of the various membrane constituents.[24] We have implicitly assumed this correlation length is smaller than ξ , viz., we have assumed a sharp boundary between the two coexisting phases. We will present elsewhere how an externally imposed curvature influences lipid segregation on membranes with this assumption violated, for example, on membranes with the temperature close to a critical demixing point.
We thank A. Travesset, P. M. Goldbart, T. C. Lubensky, and A. C. Shi for helpful discussions.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|






