†Corresponding author. E-mail: zhangweidoit@163.com
*Project supported by the Fundamental Research Funds for the Central Universities of Central South University, China (Grant No. 2014zzts145).
The influence of vacuum fluctuation and phonon bath on the probability of single photon emission are both considered in the two-level system model theoretically; by using the master equations and generating function method we get the analytical expression of the second-order fluorescence correlation function, probability of single photon emission, and Mandel’s Q parameter. The results manifest that the coupling between the phonon bath and single photon source destroys the superposition state induced by the square laser pulse, the Rabi oscillation damped rapidly with the increasing of temperature. Theoretically, when the structure parameter of arsenide quantum dots α scaled to 0.1 times of the sample, the critical coherence-temperature will rise up to hundreds of Kelvin, which means a step forward to the realization of coherent control of single photon source at room temperature.
Quantum dots (QDs) which are solid-state nanostructures are seen as excellent candidates for performing quantum information processing tasks.[1– 4] QDs will work as a single photon source (SPS)[5, 6] which means a deterministic trigger, SPS emits one and only one photon once a laser pulse interacts with it in a certain time interval T.
The single photon control problem has been studied by a two-level system (TLS) model[7, 8] theoretically. The single atom or single molecule are modeled as an isolated TLS, only influenced by radiation field (photon bath), i.e., which is the environment noise.[7– 10] For the sake of designing the optimal probability of single photon emission (PSPE) and analyzing Mandel’ s Q parameter for photon statistics, the respective analytical expressions had been discussed in previous work.[7] Since the SPS is modeled as an isolated TLS, one only considers the photon bath (which leads the master equation to the Lindblad form[11, 12]), while the solid-state systems, such as QDs, [13] individual molecules in matrix, [14– 16] or color centers in diamond[17– 19] should consider not only photon bath (vacuum fluctuation), but also phonon bath coupled with them. In these solid-state systems, the electrons– phonon coupling mechanism is a major source of optical dephasing.[20– 24] By taking this mechanism into account, we include the environment temperature effects into the problem of single photon control in solid-state SPS. This is the first theoretical work in analysis of the influence of temperature on the single photon control.
The goal of this paper is to study the influence of environment temperature on the coherent properties of photon emission and photon statistics. Both the analytical expressions of the PSPE and Mandel’ s Q parameter are derived and discussed. Our results and analyses about SPS pave the way for realization of linear optical quantum information processing at room temperature.
The rest of this paper is organized as follows. In Section 2 we present a TLS model based on the solid-state system, and generating function formalism used for the derivation of our modified generalized optical Bloch equations, then we derive the analytical expressions of the PSPE and Mandel’ s Q parameter. In Section 3 we discuss the physical meaning of those analytical expressions. In Section 4 we draw the conclusion of this paper.
Considering a single quantum dot (QD) that is modeled as a TLS, with ground-state | 0〉 and an excited-state | x〉 , which is coupled to the photon bath (vacuum fluctuation) and phonon bath, both represented by sets of harmonic oscillators, and a square laser pulse pumps the single emitter from electronic ground state | 0〉 to the excited state | x〉 . We make a semiclassical treatment of the coupling between the square laser pulse and SPSL. The Rabi frequency Ω is not so large that it dresses the states leading to Mollow’ s triplet states. With the rotating-wave approximation (RWA) on both the driving laser and system– radiation coupling terms, the Hamiltonian is
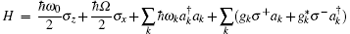
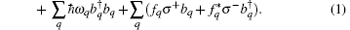
Here 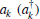
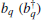
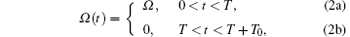
and Ω (t + n(T + T0)) = Ω (t) where n = 1, 2, ..., (see Fig. 1).
The exciton population is described by Pauli operator σ z = | x〉 〈 x| – | 0〉 〈 0| , the lowering operator σ − = | 0〉 〈 x| , and the raising operator σ † = | x〉 〈 0| . Since the fundamental band gap ħ ω 0 is much larger than κ BT, the photon field can be taken as remaining at zero temperature, only the pure dephasing process includes how the environment temperature affects the PSPE and how it destroys the coherent property of photons. Presuming the phonon bath to be in thermal equilibrium, by taking trace over the phonon modes, the spectral density
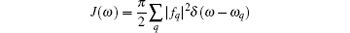
contains the entire information about the phonon bath which completely describes the interaction between the QD and phonon bath.[25] For arsenide QDs, the coupling to acoustic phonons by means of deformation potential causes the pure dephasing process that has been found to be the dominant decoherence mechanism at elevated temperature.[21– 23] An appropriate choice for the spectral function and its related cut-off frequency, can be specified by the QD environment. We adopt the model in Ref. [26] and get the spectral density function as follows:

In the model, the wave-function is determined by the spherically symmetric harmonic confinement potential for the QD, the structure constant is
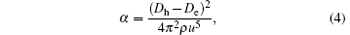
where the cut-off frequency 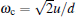
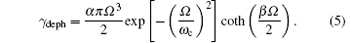
The formula manifests the influence of temperature T and Rabi frequency Ω to the pure dephasing rate. We are more interested in the high temperature situation, since the realization of SPS in high temperature will be more practical. With the temperature increasing, the first-order approximation with respect to ħ Ω /κ BT is derived by Tayler series expanding, here we consider the cutoff frequency ω c ∼ 1012 Hz which is far larger than the Rabi frequency Ω ∼ 109 Hz, then we find an approximation formula at high temperature

The functions of the pure dephasing rate with respect to the environment temperature in Eqs. (5) and (6) are shown in Fig. 2. When the κ BT is large enough in comparison with ħ Ω , the dephasing rate displays a linear relationship with the environment temperature T, which is in agreement with the result of Ref. [27]. For simplicity, we just considered the resonance situation, in the rotating frame of reference with frequency ω L, within Born– Markov approximation and RWA, the dynamic evolution of the density operator is given by[28]

The first term describes the evolution of the coupling of the driving laser to the system, δ (t) = ω o − ω L, the second term describes the influence of radiation field, [11] 𝛾 sp is the half width of spontaneous radiation rate Γ in reference, [8, 9] the third term describes the pure dephasing process caused by the coupling of phonon bath to the QD, this term includes the temperature effects into the master equations. In the resonance situation, the frequency shift caused by the phonon bath has been neglected, we obtain the stochastic Liouville equations by taking the pure dephasing process into account.[29] The main difference between the isolated system and the solid-state system is that the dynamic equation contains the third term and 𝛾 deph is temperature-dependent.
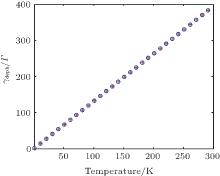 | Fig. 2. The dephasing rate function with respect to temperature. We calculated the parameters as those in Ref. [26]: De = − 14.6 eV, Dh = − 4.8 eV, d = 4.5 nm, u = 5110 ms− 1, ρ = 5370 kg· m− 3, then obtained α = 0.032 ps2. Here Ω = 10Γ , Γ = 100 MHz, the crossing and the circle represent the results of the modeled function Eq. (5) and the first-order approximation function of temperature factor Eq. (6) respectively. |
By utilizing state vectors | 0〉 and | x〉 , we expand the operator equation Eq. (7) into the following density matrix elements differential equations
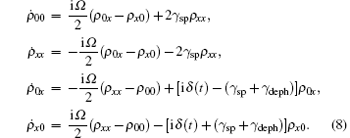
By solving the above linear coupling differential equations with initial condition (ρ 00, ρ xx, ρ 0x, ρ x0) = (1, 0, 0, 0), we obtain the time-dependent analytical expression of density matrix elements.
The definition of the second-order correlation function of a photon is
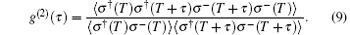
Here τ = t − T represents the time delay between the first photon and the second one, T is the time that the first photon has been recorded, g(2)(τ ) is proportional to the probability of detecting two emitted photons, separated by τ and normalized by the probability of independent detection. Since we get ρ xx(t), then utilizing the quantum regression theorem, [30, 31] we find the analytical expression of g(2)(τ ) as follows:
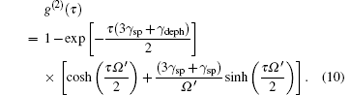
Here 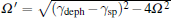
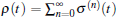
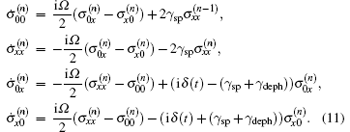
Note that σ (− 1) ≡ 0, the distinct difference compared to Eqs. (8) is the 
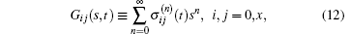
where s is an auxiliary variable which can be specified on needs. We define the generating Bloch variables as
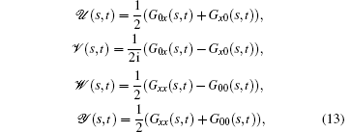
and define the vector V = (𝒰 (s, t), 𝒱 (s, t), 𝒲 (s, t), 𝒴 (s, t))T, we then get the modified generalized optical Bloch equations as

where

We solve the modified generalized optical Bloch equations in two separate time intervals with two different Rabi frequencies. At first, we consider the solution when T < t < T + T0, Ω = 0, and zero detuning frequency δ (t) = ω 0 − ω L = 0, ω 0 = ω x − ω 0. ω i(i = 0, x) represents the energy of QDs’ electrons in state | i〉 (i = 0, x). In this case, the modified generalized optical Bloch equations become

Taking the generalized Bloch vector V(s, T) = (𝒰 (s, T), 𝒱 (s, T), 𝒲 (s, T), 𝒴 (s, T))T as the initial condition, after making Laplace-transformation, and performing simple algebra operations, we derive the time-dependent generating function solution as follows:
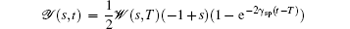

At time t = 0, the SPS is at the ground state, and the vector of the reduced density matrix elements σ (t = 0) = (1, 0, 0, 0)T. Thus, we have the initial condition of the generalized Bloch vector (𝒰 (s, 0), 𝒱 (s, 0), 𝒲 (s, 0), 𝒴 (s, 0) = (0, 0, − 1/2, 1/2, ), Ω = const., and zero detuning frequency δ L = ω L − ω 0 = 0. Now the modified generalized optical Bloch equations become
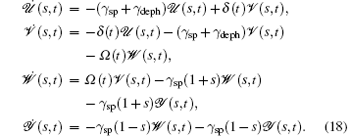
By making Laplace-transform t → z on both sides of Eqs. (18) with initial conditions given above, then transforming the differential equations to algebraic equations. The solution of the algebraic equations is given below

We could derive the initial condition of Eqs. (16) by making the inverse Laplace transform of this solution with z → T.
Here we are interested in the probability of single photon emission and Mandel’ s Q parameter. Once we get the generating function, under the condition T0 ≫ 1/𝛾 sp, we only need the solution when t → ∞
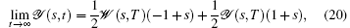
the probabilities of emitting n photons after time t (T < t < T + T0) could be obtained by SPS interacting with laser pulse in time interval T, and then we get the fractional moments of N(t). The formulas to extraction probability and fractional moments are presented below

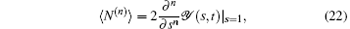
where 〈 N(n)〉 = 〈 N(N − 1)(N − 2)… (N − n + 1)〉 , (n < N). Through Eq. (21) and Eq. (22) we can derive the PSPE, the average number of N photon emission in time t, and the second-order fractional moment of N as given below
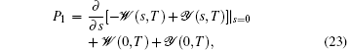
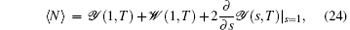
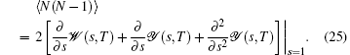
The definition of Mandel’ s Q parameter is
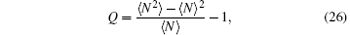
it also could be written as
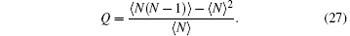
By Eqs. (20) and (23), we can derive the zero-order approximation solution of the PSPE with respect to spontaneous radiation rate 𝛾 sp as follows:

Within zero approximation, once the emitter is in the fixed pure dephasing rate, i.e., the environment temperature is small enough such that the coherence still exists, the probability will oscillate without damping, this is the unreasonable case caused by neglecting the spontaneous radiation rate 𝛾 sp. For the sake of physical reasonability, the spontaneous radiation rate 𝛾 sp should be included into the exponential part of the above formula, we thus correct Eq. (28) by including the spontaneous radiation rate 𝛾 sp. The corrected formula of the PSPE is
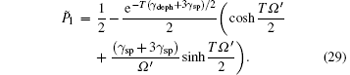
By making use of Eqs. (20), (19), (24), and (25), we can derive the analytical expressions of the first-order fractional moment and the second-order fractional moment as follows:

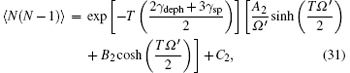
where the coefficients Ai, Bi, Ci (i = 1, 2) are given in Appendix A. By substituting Eqs. (30) and (31) into Eq. (27) we obtain the analytical expression of Q as follows:
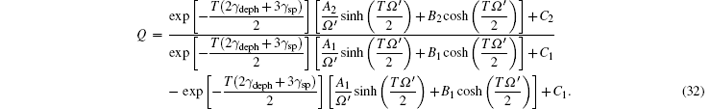
Since there must be no damping with fixed pure dephasing rate 𝛾 deph in Eq. (28), we should take the spontaneous radiation rate into consideration in deriving Eq. (28) and then obtain the corrected formula of PSPE, i.e. Eq. (29), this equation includes both the thermal fluctuation and vacuum fluctuation into the PSPE. We also discussed the influence of the laser pulse on Ω and T and showed the results in Figs. 3– 6 with Rabi frequency Ω = 10, 15, and 20 respectively, while the structure parameter is still taken as α = 0.032 ps2. Comparing these figures, we find that the oscillation increases simultaneously with Ω increasing, and 𝛾 deph needs to be larger to damp the Rabi oscillation. This indicates that with Ω increasing, the coherent property of single photon emission can be sustained in higher temperature. However, we should notice that the 𝛾 deph is affected by Ω at the same time, we could not increase the critical coherence temperature by increasing Ω , but in some reasonable range, the bigger Ω can guarantee higher critical coherence-temperature. Since coherent control of quantum light[34] will be necessary for the future high-efficiency sources of indistinguishable single photons, [35] especially its realization at room temperature. The above discussion about finding the critical coherence-temperature just throws a little light upon the problem of realization of SPS at room temperature. For the sake of finding good SPS at high temperature, we propose to find specific QD with structure parameter α , which is far smaller than the sample in our model, the temperature could get far higher than that in our situations in Figs. 4– 6, because we can see from Eq. (6) that when 𝛾 deph = const, α ∝ T− 1. Here we estimate this possibility by setting the Rabi frequency Ω = 10 in Fig. 4, the critical pure dephasing rate 𝛾 deph is about 𝛾 deph ∼ 20, then we find the critical coherence temperature in Fig. 2 is about 15 K with structure parameter α = 0.032 ps2. When α = 0.0032 ps2, we will sustain the coherent property of single photon emission at critical coherence-temperature T ∼ 150 K. Since the expression of Mandel’ s Q parameter is too cumbersome, it is not intuitional to analyze the physical meaning of this formula, we have to utilize the numerical method and plot the three-dimensional figures to show how these variables affect it straightforwardly, instead of finding a way to simplify the large expression. From the variation trend shown in Fig. 7, we could judge that equation (32) is reasonable, since there exists oscillation while the dephasing rate 𝛾 deph is small enough, which means that the dephasing process is very slow in comparison with the period of Rabi oscillation, but as the environment temperature increases, the pure dephasing rate 𝛾 deph also increases, which leads to dephasing rapidly, and the Rabi oscillation disappears with temperature increasing. We could also see that Mandel’ s Q parameter tends to about − 0.2 with the pure dephasing rate 𝛾 deph increasing. This indicates that with 𝛾 deph increasing, the photon radiation process tends to be a sub-Poissonian process.
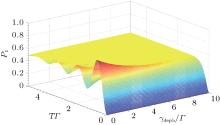 | Fig. 3. The probability of single photon emission with the influence of the laser pulse on pure dephasing rate 𝛾 deph and time interval T, where we take Γ = 2𝛾 sp = 1, and Ω = 5. |
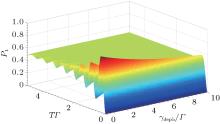 | Fig. 4. The probability of single photon emission with the influence of the laser pulse on pure dephasing rate 𝛾 deph and the width of the laser pulse. Here we take Γ = 2𝛾 sp = 1, and Ω = 10. |
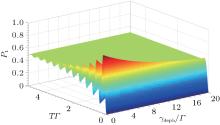 | Fig. 5. The influence of pure dephasing rate 𝛾 deph and the width of laser pulse on the probability of single photon emission. Here we take Γ = 2𝛾 sp = 1, and Ω = 15. |
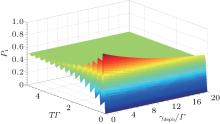 | Fig. 6. The influence of pure dephasing rate 𝛾 deph and the width of laser pulse on the probability of single photon emission. Here we take Γ = 2𝛾 sp = 1, and Ω = 20. |
 | Fig. 7. The influence of pure dephasing rate 𝛾 deph and width of laser pulse on Mandel’ s Q parameter. Here we use the same parameters as those in Fig. 3. |
In conclusion, we include not only the vacuum fluctuation but also the phonon bath into the process of single photon emission firstly. The coupling of vacuum fluctuation to a single emitter causes the population relaxation and phase destruction, [9, 36, 37] but how the temperature affects the probability and the quantum coherent property of single photon emission has not been considered in this mechanism. In this paper, we introduce the electron– phonon coupling mechanism, which causes the pure dephasing process, to explain the influence of temperature on that problem theoretically. A possible way to find practical SPS at the order of magnitudes of room temperature has also been proposed, namely nanostructure which owns smaller structure parameter α will have higher critical coherence-temperature. Our results provide a way to find excellent QDs for the realization of SPS at room temperature in theory.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|



