†Corresponding author. E-mail: gaoyc1963@heuu.edu.cn
‡Corresponding author. E-mail: wangxt45@126.com
*Project supported by the Science Director Foundation Project of the National Natural Science Foundation of China (Grant No. 11347179).
A first-principles approach is employed to study the structural, electronic, and magnetic properties of RbCa X2 ( X = C, N, and O) full-Heusler compounds. It is observed that RbCaN2 and RbCaO2 are new d0 half-metals with an integer magnetic moment of 3 μB and 1 μB in their ferrimagnetic ground states, respectively, while RbCaC2 is a common metallic compound. Analysis of the density of states of these compounds indicates that the magnetic moment and furthermore, the half-metallicity primarily originate from the spin-polarization of the p-like states of N and O atoms. The half-metallic (HM) gaps of RbCaN2 and RbCaO2 are notably large; thus, the half-metallicity is robust against lattice distortion. Such materials are suitable to be grown on various semiconductor substrates. In addition, for RbCaN2 and RbCaO2, four possible terminations of the surface are also calculated.
Different from the conventional half metallic materials, d electrons provide the primary magnetic moments for transition metals.[1– 5] In recent years, as a new class of potential materials in spintronic devices, considerable attention has been devoted to 100% spin-polarization in systems without transition. This new class of materials is usually called sp or d0 half metallic materials. From an application point of view, these materials are very promising; d0 half-metallic materials exhibit many interesting features, such as a rather large HM gap and a high Curie temperature, and are robust to the change of the lattice parameter.
A first-principles investigation of the d0 half-metallic in ZB-CaP, CaAs, and CaSb has been proposed by Kusakabe et al.[6] The magnetic order of calcium pnictides is carried by the p-electrons without any direct involvement of the d-electrons. Since then, many studies with different methods on d0 half-metallic materials with a zinc– blende structure were performed, such as I– V, II– V, and II– IV compounds.[7– 12] In detail, on the basis of ab initio calculations employing the density functional theory (DFT), Sieberer et al.[7] predicted that all I/II– V compounds have a tendency toward a ferromagnetic ground state. Furthermore, using the mean-field approximation and random-phase approximation, Gao et al.[8, 9] predicted that ZB– CaC, SrC, and BaC exhibit robust d0 half-metallic ferromagnetism with Curie temperatures higher than room temperature. Additionally, in several studies, alkali and alkaline earth metals with C/N/O-elements in various structures were also predicted to be HM materials.[13– 18]
Moreover, due to their high Curie temperature Tc, high magnetic moments, and their ability to be easily synthesized in reality, Heusler compounds[19] have also attracted considerable research interest in the spintronic field. Until now, to the best of our knowledge, there have only been a few predictions in the field of d0 half-metallic materials based on the Heusler structure. Furthermore, a very large pool of interesting materials is waiting for exploration. Chen et al.[20] and Malsawmtluanga et al.[21] reported that GeKCa and SnKCa were d0 half-metallic materials in the half-Heusler structure with magnetic moments of 1 μ B per formula unit. Biał ek et al.[22] have investigated the surface properties of GeKCa and SnKCa by first principle calculations and showed that their bulk half-metallicity is destroyed at the surfaces, terminated with metal atoms. Umamaheswari et al., [23, 24] Lakdja et al., [25, 26] Rozale et al., [27, 28] and Wei et al.[29] also predicted ferromagnetism on the half-Heusler RbSrX (X = C, Si, and Ge), XCsBa (X = C, Si, and Ge), XCaC (X = Li and Na), and XRbCs (X = N, P, and As).
Recently, the bulk and surface half-metallicity of full-Heusler compounds KCaX2 (X = C, N, and O) have been investigated by Rozale et al.[30] and Biał ek et al., [31] respectively. Furthermore, Umamaheswari et al. have predicted RbCaN2 and RbCaO2 to be HM materials.[32] However, the effects of the lattice parameters on the electronic structure and the surface properties of the materials were neglected in the discussion. The origin of the magnetism, especially the half-metallicity, should be explained in a more detailed way based on the electronic arrangement. In this paper, we calculated the electronic structures and magnetic properties of the RbCaX2 compounds in the full-Heusler structure. Our calculations show that the RbCaN2 and RbCaO2 compounds are both typically half-metallic materials with a large HM gap. In addition, the stability of the half-metallicity and the d0 surface half-metallic properties of the materials, which were neglected in the discussion of Umamaheswari’ s work, have been addressed based on the electronic structures. The origins of the magnetism and half-metallicity have been discussed in detail based on the electronic arrangement.
The CASTEP code was used to calculate the band structures, density of states (DOS), and the total energy. The CASTEP code is based on the density functional theory (DFT) plane-wave pseudo-potential method.[33, 34] During our calculations, the ultrasoft pseudo-potential[35] was used to describe the interactions between the valence electrons and the atomic core, and the exchange– correlation potential was dealt with by the generalized-gradient approximation (GGA) in the scheme of Perdew– Burke– Ernzerh (PBE).[36, 37] The cut-off energy of the plane wave basis set is 450 eV for all of the cases. For the Brillouin zone integration, we use 13× 13× 13 k meshes for the bulk RbSrN2 and 10× 10× 1 k meshes for the (001) surfaces, respectively. The calculations continue to ensure good convergence until the energy deviation is less than 1× 10− 6 eV/atom. The (001) surfaces of RbCaN2 and RbCaO2 were studied by adopting a slab model that included 11 atomic layers for both, which were terminated. One 15-Å vacuum was applied to avoid the interaction of adjacent slabs.
From the structural point of view, Heusler compounds (molecular formula X2Y Z) have two possible structures, namely, a Cu2MnAl-type structure and an HgCu2Ti-type structure. In the former, the atomic sites are as follows in Wyckoff coordinates: X(A) (0, 0, 0), Rb(B) (1/4, 1/4, 1/4), X(C), (1/2, 1/2, 1/2), and Ca(D) (3/4, 3/4, 3/4), and in the latter, X(A) (0, 0, 0), X(B) (1/4, 1/4, 1/4), Rb(C) (1/2, 1/2, 1/2), and Ca(D) (3/4, 3/4, 3/4). The two possible prototype structures for crystallization of the full-Heusler compounds Cu2MnAl and Hg2CuTi are displayed in Figs. 1(a) and 1(b). To find the more favorable structure in RbCaX2, the total energy is minimized according to two possible prototype structures, as shown in Fig. 2. It can be observed that all of the compounds have a lower total energy in the Cu2MnAl-type structure than in the Hg2CuTi-type structure at the equilibrium lattice constant. Thus, from the point of view of the total energy, the Cu2MnAl-type structure is energetically more favorable for RbCaX2. The achieved equilibrium lattice constants are 6.64 Å , 6.47 Å , and 6.34 Å for RbCaX2 (X = C, N, and O) with the Cu2MnAl-type structure, respectively.
 | Fig. 2. The calculated total energies as a function of the lattice constants for RbCaC2 (a), RbCaN2 (b), and RbCaO2 (c) with Hg2CuTi-type and Cu2MnAl-type structures. |
Note that not all of the Heusler alloys can be synthesized and form a stable phase. To examine whether the Cu2MnAl-type RbCaX2 compounds can be synthesized in the experiment and the phase stability, the formation energy Eformation was calculated by subtracting the sum of the equilibrium total energies for constituent elements from the equilibrium total energies of the corresponding compound under current study. Using the formula: Eformation = (Etol– 2EX– ERb– ECa), we find that the Eformation of the RbCaN2 and RbCaO2 compounds are − 1.39 eV and − 0.83 eV, respectively; however, the Eformation of the RbCaC2 compound is 5.73 eV. Note that the negative eV indicates that the compound is energetically stable. Thus, it is possible to synthesize the RbCaN2 and RbCaO2 compounds with Heusler structure experimentally.
The electronic structures of the RbCaX2 compounds along the main symmetry directions in the irreducible Brillouin zone are shown in Fig. 3. For RbCaC2, we can see that both the majority- and minority-band structures show a metallic overlap with the Fermi level (Ef), which indicates that RbCaC2 is a common metallic material at its own equilibrium lattice constant. However, for RbCaX2 (X = N and O), the Fermi levels are located at a band gap in the majority spin direction and have an intersection with the valence bands in the minority spin direction, which indicates that the RbCaX2 (X = N and O) compounds are half-metallic materials. We can see that the energy gap in these compounds is an indirect band gap (G– X) and that the indirect band gap is equal to 3.71 eV and 4.39 eV for RbCaN2 and RbCaO2, respectively. The spin-flip gaps (HM gap), which are the minimum energy required to flip a minority-spin electron from the valence band maximum edge to the majority-spin Fermi level, are the most proper indication of the half-metallicity of a material.[37] The width of the HM gaps are EHM− gap (RbCaN2) = 0.71 eV and EHM− gap (RbCaO2) = 0.49 eV, respectively. This value is quite a lot larger than most of the half-metallic Heusler compounds with 3d transition metals; it is also larger than the previously d0 half-metallic Heusler compounds KCaN2 (0.16 eV) and KCaO2 (0.30 eV), which indicates that the half-metallicity of the RbCaX2 (X = N and O) compounds is very stable.
Figure 4 shows the calculated total and partial density of states (DOS) of the RbCaX2 (X = N and O) compounds to further understand the origin of the magnetism and half-metallicity. In a range of − 4 eV ∼ 2 eV/− 4 eV ∼ 1 eV, the DOS of the Rb and Ca atoms with s, p, and d orbitals have little distribution for both spin channels. The states around − 4 eV ∼ 2 eV/− 4 eV∼ 1 eV can mainly be traced to the covalent hybridization between the p-states of N(A)/O(A) and N(C)/O(C). The origin of the gap is similar to those of sp HM ferromagnets of alkaline-earth nitrides and carbides and mainly attributed to the covalent hybridization between the p-states of N(A)/O(A) and N(C)/O(C).[8, 9] The calculated total magnetic moment of the RbCaN2 (RbCaO2) compound is 3 μ B (1 μ B). This can be explained from the electronic arrangement: there are 13 (15) valence electrons in RbCaN2/RbCaO2 compounds (Rb: 5s1; Ca: 4s2; N: 2s2, 2p3; O: 2s2, 2p4) that contribute to the bond formation and magnetism. In detail, 4 valence electrons occupy the N-2s and O-2s states in the lowest energy states. 6 of the remaining 9 (11) valence electrons occupy the majority spin p states of N/O, which results in the 6 fully filled majority spin bands. The remaining 3 (5) valence electrons partially occupy the 6 lowest minority spin bands by leaving 3 (1) holes, which are responsible for the magnetic moments of 3 μ B (1 μ B), respectively. Further, for RbCaN2/RbCaO2, the atomic magnetic moments are 1.62 μ B/0.56 μ B for N(A and C)/O(A and C), − 0.16 μ B/− 0.08 μ B for Rb(B), and − 0.08 μ B/− 0.04 μ B for Ca(D), respectively. The magnetic moment of the N(A and C)/O(A and C) atom is antiparallel to that of the Rb(B) atom, which is a typical characteristic of half-metallic (HM) ferrimagnets.
Here, we will study the robustness of the half-metallicity with respect to the lattice constant. The surroundings (e.g., the temperature) and the preparation methods (e.g., the growth of thin film materials) usually make the lattice of the half-metallic materials change and cause the lattice constant to deviate from the ideal one, which may affect their half-metallicity. The DOSs at different lattice constants were investigated for the RbCaN2/RbCaO2 compounds. As shown in Fig. 5, we find that the electronic structures are similar to those at the equilibrium lattice constants, and both the valence band and conduction band shift upwards with the decrease of the lattice constants. From the figure, it can be observed that the half-metallicity could be kept until the lattice constants are compressed to a critical value of 5.37 Å and 4.94 Å for the RbCaN2/RbCaO2 compounds, respectively. This means that the half-metallicity is preserved up to a contraction of the lattice constant by 17% and 22% for RbCaN2/RbCaO2, respectively.
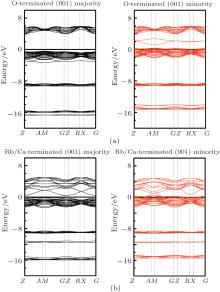
Considering the application of these compounds in electronic devices, one cannot forget a description of the surface properties of the materials. The electronic properties of surfaces usually differ from those of the bulk. How much different the surface properties are from those of the bulk depends on, among other factors, surface termination. The surface usually destroys the half-metallicity and decreases the spin polarization[22, 31] in practical spintronic applications. The corresponding crystal structures are also shown in Figs. 1(c) and 1(d). Finally, we calculated the surface electronic structure to check the half-metallic properties of the RbCaN2/RbCaO2 compounds, as shown in Figs. 6 and 7. For RbCaN2, we can see that the N terminated (001) surface is still half-metallic; however, the half-metallic gap in the majority spin direction is destroyed by the Rb– Ca terminated (001) surface. The calculated spin polarization ratio is 66.7% at the Rb– Ca terminated (001) surface and loses the 100% spin polarization rate of the bulk state. However, for RbCaO2, both the O and Rb– Ca terminated (001) surfaces are still half-metallic.
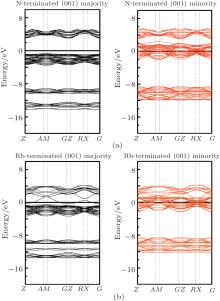 | Fig. 6. Majority-spin and minority-spin band structures of the N and Rb– Ca terminated (001) surfaces of the RbCaN2 compound. |
To summarize, we have studied the magnetic and half-metallic properties of the RbCaX2 (X = C, N, and O) full-Heusler alloys. d0 half-metallicity has been predicted in the Cu2MnAl-type RbCaN2/RbCaO2 compounds by first-principles calculations, while RbCaC2 is a common metallic compound. RbCaN2/RbCaO2 compounds have quite large HM gaps, and their half-metallicities are not sensitive to lattice expansion and contraction. In the RbCaN2/RbCaO2 compounds, the magnetic moments of N(A)/O(A) and N(C)/O(C) atoms are the same and antiparallel to that of the Rb(B) atom; thus, RbCaN2/RbCaO2 are HM ferrimagnets. The magnetic moments of RbCaN2/RbCaO2 are 3 μ B and 1 μ B, respectively, and they mainly originate from the spin-polarized p-like states of N and O atoms. For the four possible terminations of the surface, the half-metallicity is lost in the case of the Rb– Ca terminated (001) surface of RbCaN2.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|
| 32 |
|
| 33 |
|
| 34 |
|
| 35 |
|
| 36 |
|
| 37 |
|