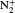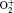†Corresponding author. E-mail: wangdez@dlut.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 10775026, 11275042, 11305026, and 11405042).
In this paper, the characteristics of an atmospheric pressure helium plasma jet generated by a dual-power electrode (DPE) configuration are investigated by using a two-dimensional fluid model. The effect of a needle electrode on the discharge is studied by comparing the results of the DPE configuration with those of the single ring electrode configuration. It is found that the existence of the needle leads to the generation of a helium plasma jet with a higher propagation velocity, higher species density, and larger discharge width. Furthermore, the influences of the needle radius and needle-to-ring discharge gap on the generation of a plasma jet are also studied. The simulation results indicate that the needle electrode has an evident influence on the plasma jet characteristics.
Over several decades, atmospheric pressure plasma jets (APPJ) have aroused increasing interest in low-temperature plasma research due to their extensive applications, including material processing, pollution control, and biomedical applications.[1– 4] For the development and optimization of these applications, various types of APPJ devices with different configurations or power sources have been developed and investigated. The APPJ device with dual-power sources is one of those devices, and it is the focus of this paper.
The dual-power source, including the dual frequency power source and dual-power electrodes source (DPE), has been widely used in the atmospheric pressure plasma (APP) to improve discharge efficiency and obtain higher plasma density. Now the APP driven by the dual-power sources is attracting growing attention, and some specific experiments have been reported recently. Qian et al.[5, 6] developed a dual-power electrode atmospheric pressure argon plasma jet, and investigated the effect of driving frequency on discharge characteristics. Kim et al.[7] studied a dual frequency atmospheric pressure corona plasma, and found that the length of the plasma jet, current density, and electron excitation temperature increased as a result of the dual frequency. Zhou et al.[8] used a combination of 50 kHz/2 MHz dual frequency power sources to generate an APPJ, which exhibited the advantages of both low frequency and radio frequency plasmas. Since the physical mechanism of APP driven by a dual-power source is very difficult to completely understand only through experiment measurement due to the limitation of diagnostic techniques, numerical simulation provides a very important alternative tool. Waskoenig and Gans[9] numerically investigated plasma ionization and associated mode transitions in dual radio-frequency (RF) driven APP. O’ Neill et al.[10] used a multi-scale numerical model to investigate the influence of dual frequency excitation on the effective electron energy distribution function in a dual RF driven APP. Wang et al.[11] demonstrated that the plasma intensity in the RF discharge could be enhanced drastically when an additional low-duty-ratio pulse source was applied to the discharge. However, little simulation work of the APPJ driven by dual-power sources has been done so far. Thus, some physical properties of the APPJ are still unclear and further study is required.
In this paper, as a first step of study, a two-dimensional fluid model[12, 13] is used to study the physical properties of the APPJ driven by DPE. The device is similar to that developed in experiments.[5, 6] The characteristics of the APPJ driven by DPE are simulated and compared with the single ring electrode case in order to identify the advantages of the DPE plasma jet, namely, the effect of the needle electrode. Besides, the influences of needle parameters, i.e., needle radius and needle-to-ring discharge gap, on discharge characteristics are also studied.
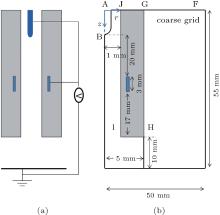
The setup of the plasma jet described in this paper is shown in Fig. 1(a). A metallic needle anode is immersed in a thin dielectric tube with an inner radius of 1 mm and outer radius of 5 mm. The relative permittivity of the dielectric tube is 2. The working gas of helium flows through the dielectric tube to ambient air. The needle tip is assumed to be of a semi-sphere with a radius of 0.5 mm. A thin ring electrode of 3 mm in width and 0.3 mm in thickess is embedded in the dielectric tube with a distance of 2 mm from the axis of symmetry. The downstream ring electrode is 17 mm above the tube exit. The distance between the tip of the needle and the ring electrode is 20 mm. A 6-kV positive voltage is applied to both the needle and the ring, which form the so-called “ double-power” electrode. The voltage is a square wave ‘ pulse’ and only one pulse discharge is simulated, i.e., it reaches the peak voltage instantaneously at the beginning of the simulation and remains constant during simulation. A grounded electrode is placed 10 mm away from the tube exit. Our model is divided into two parts: a neutral gas flow model and a plasma dynamics model. Two models are described below, respectively.
Figure 1(b) shows the simulation geometry used in this paper. The working gas flows into the domain from the boundary between the needle and the dielectric tube (i.e., AJ in Fig. 1(b)). The composition of ambient air is simplified into 80% N2 and 20% O2. The governing equations for the neutral gas flow model consist of the mass continuity equation, the momentum conservation (Navier– Stokes) equations and the species transport equation as follows:
(i) The mass continuity equation is
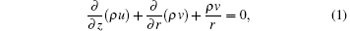
where ρ is the density (helium 0.1664 kg· m− 3, air 1.293 kg· m− 3), u and v are the velocity components in the axial and radial directions, respectively.
(ii) Momentum conservation (Navier– Stokes) equations can be written as
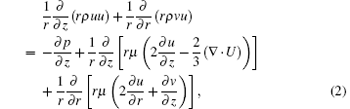

where p is the pressure, μ is the viscosity coefficient (helium 1.94 × 10− 5 Pa· s and air 1.82 × 10− 5 Pa· s), and U is the velocity vector of gas flow.
(iii) The species transport equation is
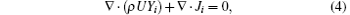
where Yi is the local mass fraction of each species, and Ji is the diffusion flux of species i. When the flow is laminar, the diffusion flux can be written as
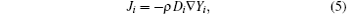
where Di is the diffusion coefficient for species i in the mixture (helium in air 7.2 × 10− 5 m2· s− 1). Moreover, the gas flow state inside the tube which is laminar or turbulence flow is usually determined by the Reynolds number, and defined as
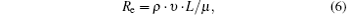
where υ is the average velocity of the gas and L is the characteristic length.
The governing equations (1)– (4) are solved using a stationary solver in COMSOL. The boundary conditions are summarized in Table 1, [14, 15] and the corresponding boundaries are also illustrated in Fig. 1(b). The radial uniform He velocity at inlet AJ is given, and the direction of inlet velocity is normal to the boundary AJ. Generally speaking, the natural convection velocity is about 0.1 m/s– 0.3 m/s in an aeration room with an air conditioner.[14] Therefore, in our simulation, we assume the natural convection velocity to be 0.3 m/s at the air inlet GF to simulate the He flow more accurately.
| Table 1. Boundary conditions for the neutral gas model. The symbols (A– J) correspond to the vertices in Fig. 1(b). The unit 1 atm = 1.01325 × 105 Pa. |
In this section, based on the model described previously, the simulation results are presented and discussed. First, the characteristics of the APPJ driven by DPE are studied. Then, the simulations of the APPJ driven by the single ring electrode are shown and the results are compared with those of the DPE case to investigate the effect of the needle electrode. Finally, the influences of needle parameters on the APPJ are analyzed.
Figure 2 shows the results of gas flow simulation in a steady state. As can be seen in Fig. 2, the helium mole fraction is almost 1 inside the tube. From the tube exit to the ground electrode, due to the mixing of the ambient air with the helium gas flow, a helium– air mixing layer is created, which is essential for the propagation of the plasma jet. The gas velocity of the axial component slows down after the helium gas leaves the dielectric tube, and the air mixture ratio increases with the distance from the tube exit. When the helium gas flow reaches the ground electrode, it flows radially along the surface of the electrode, which is similar to the simulation results presented in Ref. [21].
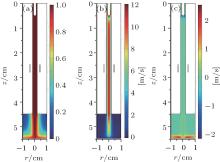 | Fig. 2. Results of gas flow calculation: (a) helium mole fraction, (b) gas velocity component in the axial direction, and (c) gas velocity component in the radial direction. |
Figure 3 shows the Laplacian electric field and electric potential distributions on the axis of the discharge setup for DPE. Owing to the small radius of curvature, the electric field is very high near the needle tip and is positive due to the positive voltage applied. The electric field decreases rapidly along the axis and its value is zero at the position z = 1.3 cm. There are two peak values of electric field located at the edges of the ring electrode, and then the electric field decreases to zero. It is noted that the peak value of electric field at the upstream edge (left edge in Fig. 3) of the ring electrode is negative, while that at the downstream edge (right edge in Fig. 3) is positive. This can also be explained by the potential distribution.
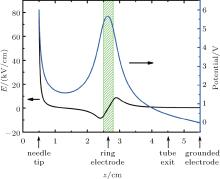 | Fig. 3. Laplacian electric field and electric potential distributions on the symmetry axis. The filled region represents the position of the ring electrode. |
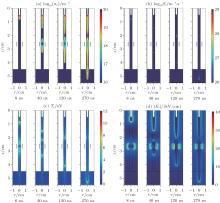
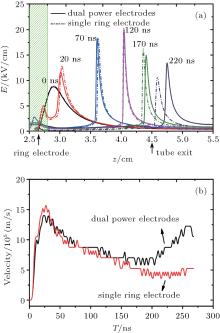
The plasma jet characteristic parameters (electron density, total ionization rate, and mean electron temperature) and absolute value of electric field distribution evolutions are shown in Fig. 4. During the first 8 ns, the discharge is ignited in the needle tip region first, where the Laplacian field strength is much higher than that at the other position as shown in Fig. 3, and starts to propagate inside the tube with a tubular structure towards the ring electrode. At t = 8 ns, the ionization front is between the needle tip and the ring electrode. The maximum mean electron temperature and absolute value of electric field appear in the ionization front with values about 11 eV and 40 kV/cm, respectively. Then at t = 40 ns, another intense discharge is located at the edges of the ring electrode, which is also observed in experiments.[22, 23] Two positively charged ionization fronts propagate toward each other with the decrease of discharge radius between the needle tip and ring, and a positively charged ionization front (ring downstream plasma plume) propagates toward the ground electrode between the ring and ground electrode. The decrease of the discharge radius is due to the sheath formed near the dielectric tube inner surface, which can shield the plasma channel from the tube surface.[20] At t = 120 ns, the ionization front of the needle merges with that of the ring, and a discharge channel is created. The dynamics of the mergence process has been investigated in a previous study.[13] With the progress of the ring downstream plasma plume, the discharge front leaves the dielectric tube and propagates along the helium– air mixing layer, forming a plasma jet at t = 270 ns. The maximum mean electron temperature and absolute value of electric field appear in the ionization front with values of about 7 eV and 24 kV/cm, respectively.
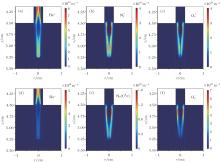
Figure 5 shows the calculated spatial distributions of species densities in the region outside of the dielectric tube at t = 270 ns after the start of pulse excitation. Because of the off-axis maximum of the ionization rate, it can be seen from Figs. 5(a)– 5(f) that the maximal densities of the species are shifted some distance from the axis for all the species, and they also tend to decrease along the axis when the discharge front leaves the tube exit. The constriction effect of the ring-shaped zone with increasing the distance from the tube exit can be attributed to air mixing, which has also been observed in experiment.[19] Note that the densities of the metastable species (He* and N2(C3π )) in the plasma jet are much higher than the charged species densities, which is consistent with the experimental results based on the optical emission spectrum.[24]
In this subsection, to investigate the influence of the needle electrode on the discharge characteristics, we first remove the needle electrode and simulate the plasma jet driven only by a single ring electrode under otherwise identical parameter conditions. The electron density and the total ionization rate are presented and compared with the results obtained with the needle electrode in Fig. 4. For simplicity, we ignore the change of the spatial distribution of helium mole fraction caused by removal of the needle.
Figure 6 shows the time evolutions of electron density and the total ionization rates of the plasma jet driven by the single ring electrode. Due to the absence of the needle, no discharge breakdown occurs in the first 8 ns. From 40 ns to 120 ns, the discharge is ignited at the edges of the ring and two ionization fronts propagate symmetrically outside the ring with the decrease of the discharge front radius. While in the case of DPE, the propagations of the two ionization fronts are asymmetrical, the intensity, and propagation velocity of the ionization front propagating upward (ring upstream plasma plume) decrease because of the effect of needle discharge.[13] At t = 270 ns, the ring downstream plasma plume leaves the dielectric tube and propagates at a distance of about 3 mm from the tube exit. It should be noted that the plasma jet propagates at a distance of about 7.5 mm from the tube exit in the case of DPE at the same time moment as shown in Fig. 4(a). This implies that the existence of a needle can accelerate the propagation of the plasma jet.
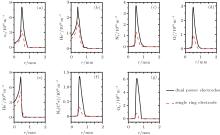
A comparison of species density distribution along the r axis at a distance of 0.2 cm from the exit of the nozzle (lines in Figs. 4(a) and 6(a)) between two kinds of electrode structures is given in Fig. 7. In both cases, the peaks of species densities are shifted some distance away from the axis, and nearly at the same position for both electrode configurations. The species densities are higher in the case of DPE, especially for N2(C3π ) and 
To further investigate the underlying mechanisms of a DPE plasma jet discharge, we plot the axial profiles of the electric field evolution and the propagation velocity of the ionization front during the propagation of the ring downstream plasma plume for two kinds of electrode configurations in Fig. 8. The propagation velocity of the discharge for DPE is much faster than that for a single ring electrode after 120 ns. It can be seen from Fig. 8(a) that the maximum field decreases more slowly in the case of DPE from 120 ns to 220 ns. As mentioned above, the ionization fronts of the needle merge with that of the ring and a discharge channel is thus created at time t = 120 ns as shown in Fig. 4. The existence of the needle can affect the discharge characteristics of the ring downstream plasma plume only after the needle discharge has been connected with the ring upstream plasma plume.
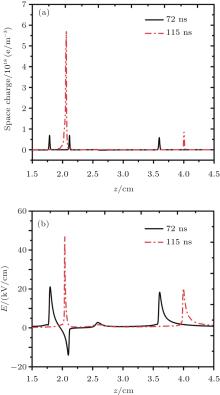
To explain why the ionization front of the ring downstream plasma plume is enhanced when the needle discharge merges with the discharge at the ring electrode, the axial profiles of the space charge and the electric field at t = 70 ns (the time before mergence) and 115 ns (when it begins to merge) are plotted in Fig. 9. From Fig. 9(a), it can be seen that after the needle discharge interacts with the discharge at the ring, a large number of positive space charges collect at the mergence location (corresponding to the strong electric field at z = 2 cm in Fig. 9(b)), which can be seen as a “ virtual anode” . This “ virtual anode” will generate an electric field, which enhances the total electric field in the ionization front from the ring electrode, as shown in Fig. 9(b). Consequently, the ionization front is enhanced and the propagation velocity of the plasma jet increases.
As mentioned above, we can see that the existence of the needle has a significant effect on the characteristics of the helium plasma jet. Therefore, it is of interest to study the influences of the needle parameters on the helium plasma jet to further optimize the design of a plasma jet source.
First, we study the influence of the needle radius on the discharge by changing the needle radius from 3 mm to 8 mm. Figure 10 shows the comparison among electron densities at t = 270 ns after the start of pulse excitation. As shown in Fig. 10(a), a smaller needle radius results in a higher electron density in the region close to the needle. However, it is a surprise that the radius of the needle insignificantly affects the structure and propagation of the plasma jet. The values of length, density, and discharge width of the plasma jets are basically the same for needles with different radii.
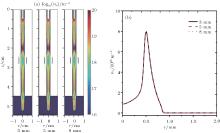 | Fig. 10. Comparison of electron density among different needle radii at 270 ns after the start of pulse excitation: (a) two-dimensional distributions of electron density, (b) radial distribution of electron density at 0.2 cm from the exit of the nozzle (line in plasma jet of Fig. 10(a) indicates the position of the radial profile). |
To explain this phenomenon, we plot the axial distributions of the electric field at several times for different needle radii (3 mm, 5 mm, and 8 mm). As can be seen from Fig. 11, the initial field (Laplacian field at t = 0 ns) close to the needle tip can be significantly larger for a smaller radius (similar with Ref. [25]), which only affects the initial stages of the needle discharge. In general, the physical shape of the needle electrode has little influence on the propagation process of discharge, which is in agreement with the results obtained in Ref. [26]. Varying the needle radius only has an effect on the electron density close to the needle tip in the dielectric tube, but has a relatively low influence on the characteristics of the helium plasma jet.
 | Fig. 11. Axial profiles of the electric field at several time moments for different needle radii, (a) 3 mm, (b) 5 mm, and (c) 8 mm. |
Then, the influence of the needle-to-ring discharge gap on the plasma jet is investigated by changing the distance from 0.5 cm to 2 cm. The simulated electron density profiles for four cases are shown in Fig. 12, indicating that the needle-to-ring discharge gap has two principal effects on the characteristics of the plasma jet. First, a smaller needle-to-ring discharge gap results in a longer plasma jet in ambient air. As shown in Fig. 12(a), the plasma jet length is 4.2 mm in the 2-cm discharge gap case, 5.3 mm in the 1.5-cm case, 6.5 mm in the 1-cm case, and 7.7 mm in the 0.5-cm case, at t = 240 ns. The second effect of discharge gap is that the density and discharge width of the plasma jet increase with the decrease of the discharge gap. All these can be attributed to the less time required for the needle discharge front and ring upstream front to merge in the case of a smaller distance.
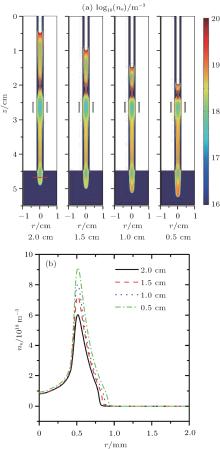 | Fig. 12. Comparison of electron density among different needle-to-ring discharge gaps at 240 ns after the start of pulse excitation: (a) two-dimensional distributions of electron density, (b) radial distributions of electron densities at 0.2 cm from the exit of the nozzle (line in plasma jet of Fig. 12(a) indicates the position of the radial profile). |
Depending on the plasma jet configuration, the plasma jet characteristics may have signigicant difference. In this paper, based on a two-dimensional fluid model, we present a detailed simulation study of an atmospheric pressure helium plasma jet generated with the DPE configuration. This work focuses on the effect of the needle electrode on the plasma jet characteristics. The numerical results show that the plasma jet has a number of features including higher propagation velocity, higher electron density, and larger discharge width than the plasam jet generated only by the single ring electrode configuration. In addition, the influence of the needle parameters on the characteristics of the plasma jet is also investigated. We find that the physical shape of the needle (different needle radii) has some effects on the plasma jet characteristics during the initial stage of the needle discharge formation, whereas the plasma jet characteristics outside the tube are relatively unaffected. Besides, the needle-to-ring discharge gap has a significant influence on the plasma jet characteristics. When the discharge gap decreases, the length, density, and discharge width of the plasma jet increase.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|