In recent years different quantization approaches such as the damped polarization model^{[1– 5]} and the phenomenological method^{[6– 10]} for the electromagnetic field in absorptive and dispersive medium have been developed. The damped polarization model to quantize the electromagnetic field is a canonical quantization in which the medium is represented by a collection of interacting matter fields and the absorptive characteristic of the medium is described by the interaction of the matter fields with a heat bath containing a continuum of reservoir fields.^[1] Based on this method, the canonical quantization of the electromagnetic field in many complex systems such as inhomogeneous absorptive dielectrics, ^[2] inhomogeneous magnetoelectric medium, ^[3] anisotropic magnetodielectric medium, ^[4] and non-dispersive bi-anisotropic magnetodielectric medium^[5] have been investigated.

The phenomenological scheme has been formulated on the basis of the fluctuation– dissipation theorem.^[6] The noise electric and magnetic polarization densities are added to the classical constitutive equations of the medium and these equations are taken as definitions of electric and magnetic polarization operators. The noise polarizations are related to two independent sets of bosonic operators. The commutation relations are imposed on the bosonic operators such that the electric and magnetic fields satisfy the correct commutation relations in agreement with quantum electrodynamics (QED). Combination of the Maxwell equations and the constitutive equations in the frequency domain gives the electromagnetic field operators in terms of the noise polarizations and the classical Green tensor. This quantization approach covers dispersive and absorptive dielectric medium, ^[6] left-handed materials, ^[7] arbitrary linearly responding medium, ^[8] anisotropic dielectrics, ^[9] multilayer system with magnetodielectric metamaterials, ^[10] etc.

Recently, the metamaterials have attracted a great deal of attention from both theoretical and experimental sides. The metamaterials have the artificial structures and the electromagnetic parameters are dependent on the resonances of the electric field and the magnetic field. These media exhibit a number of unusual electromagnetic properties such as negative refractive index, ^[11] amplification of evanescent wave, ^[12] subwavelength cavity resonator, ^[13] zero averaged refractive index band gap, ^[14] etc. Due to the fact that the unit resonance structures of metamaterials are usually anisotropic, ^[11] people were interested in the anisotropic properties and revealed many intriguing phenomena in different kinds of anisotropic metamaterials.^{[15– 21]} In classical electrodynamics, the properties of anisotropic materials are significantly different from those of isotropic materials. Thus it is meaningful to study the propagation of the quantized radiation through the anisotropic metamaterials. 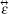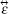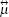While formalisms were previously available for an anisotropic medium with just permittivity tensor , ^[9] those formulas cannot be directly applied to the present metamaterials with both and as anisotropic tensors. The noise magnetization operator associated with the magnetic losses is necessary for introducing the amplitude operators of the electromagnetic field.

In the present work, we generalize the phenomenological method to quantize the electromagnetic field in the anisotropic magnetodielectric metamaterials and explore the possibility of the anisotropic magnetodielectric metamaterials to control the polarization of the quantized electromagnetic wave. The rest of this paper is arranged as follows. In Section 2, the basic equations of the quantum radiation in an anisotropic magnetodielectric medium are derived. We obtain input– output relations of quantized radiation through a single slab structure in Section 3. The numerical results and discussion are described in Section 4. Finally the main points of the paper are summarized in Section 5.

We start with the quantization of the electromagnetic field in the bulk homogeneous anisotropic medium. The operator-valued Maxwell equations for anisotropic medium free of external sources in frequency space are given as follows:^[6]

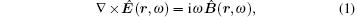
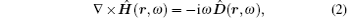
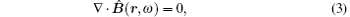
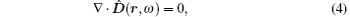
where

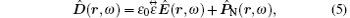
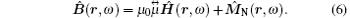
The relative permittivity tensor and relative permeability tensor of the anisotropic medium are given by

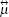
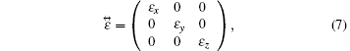
and

For absorbing anisotropic medium, ε _j, μ _j (j = x, y, z) are complex numbers dependent on frequency. Here P̂ _N (r, ω ) and M̂ _N (r, ω ), which respectively are the noise polarization operator associated with the electric losses and the noise magnetization operator associated with the magnetic losses due to material absorption, can be represented as

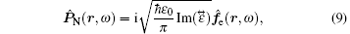
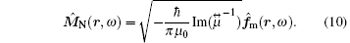
The Bosonic vector operators f̂ _e (r, ω ) and f̂ _m (r, ω ) satisfy the commutation relations (λ , λ ′ = e, m)

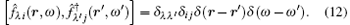
It can be shown that the fundamental commutation relations of QED are preserved:

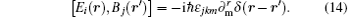
Then the noise current density ĵ _N (r, ω ) and the noise charge density ρ ̂ _N (r, ω ) fulfill the continuity equation

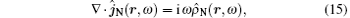
with

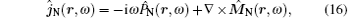
and

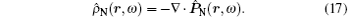
Substituting Eqs. (5), (6), and (1) into Eq. (2), we obtain the following equation:

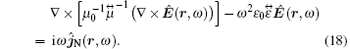
Introducing the vector potential  (r, ω ) = (iω )^{− 1}Ê (r, ω ), we have

The solution of Eq. (19) can be given by

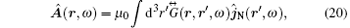
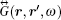
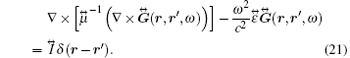
where is the Green tensor satisfying the equation

Here

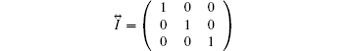
is the unit tensor.

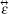
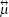
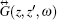
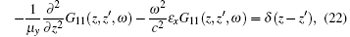
We consider a single slab of anisotropic metamaterial with the permittivity tensor and permeability tensor as Eqs. (7) and (8) embedded in the dielectric background (air). Assuming the electromagnetic waves to be linearly polarized along the x direction and y direction travel along the z direction, the corresponding elements of the Green tensor in the anisotropic medium (z ∈ [z₁, z₂]) will satisfy

Solving Eqs. (22) and (23), we obtain

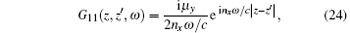
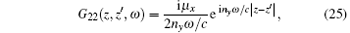
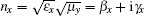
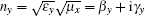
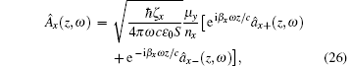
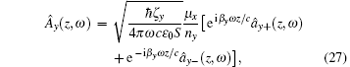
with and . Then the vector potentials for different polarized waves can be written as

where the amplitude operators are defined as

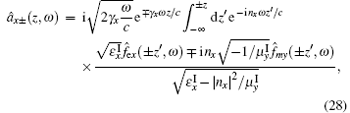
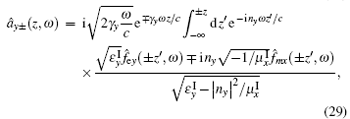
with

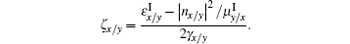
The operators â _x/y± (z, ω ) describe the amplitudes of the x/y-polarized wave propagating to the right side (the subscript + ) and left side (the subscript − ) respectively. Obviously the operators â _x/y± (z, ω ) are determined by both the Bosonic field f̂ _e (z, ω ) and f̂ _m (z, ω ) for the anisotropic magnetodielectric metamaterial. This is the main difference for the quantization of the wave in the anisotropic magnetodielectric metamaterials from that in the anisotropic dielectric materials. The S is the normalization area perpendicular to the z direction. The superscript ' I' represents the imaginary part of the corresponding physical quantity. For the dielectric background (μ _x = μ _y = μ _z = 1), we have 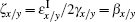which is consistent with that in the original Ref. [6].

In order to obtain the input– output relations, we define the operators â _ix/y± ≡ â _x/y± (z = z₁, ω ) to represent the incoming fields (+ ) and outgoing fields (− ) polarized in the x/y-directions from the left side of the anisotropic metamaterial. The operators â _ox/y± ≡ â _x/y± (z = z₂, ω ) correspond to the incoming fields (− ) and outgoing fields (+ ) from the right side. The relations between â _ox/y± and â _ix/y± are determined by Eqs. (26) and (27) with the boundary continuity conditions of the vector potential  (z, ω ) at the interfaces z = z₁ and z₂. After some derivations, the input– output relations for the amplitude operators for the single layer structure can be obtained as

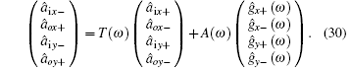
The elements of the matrix T(ω ) are listed in Appendix A. The reflectance for linearly polarized wave along the x direction and y direction are respectively defined as R_x = | â _ix− /â _ix+ | ² = | T₁₁ (ω )| ² and R_y = | â _iy − /â _iy+ | ² = | T₃₃(ω )| ².

First we consider a single layer structure composed of the anisotropic metamaterial with permittivity and permeability given by Ref. [20]:

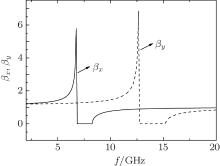
where f = ω /2π is the frequency measured in gigahertz. Such a metamaterial can be achieved experimentally by using a periodic array of H-shaped metallic pattern printed on a circuit board slab, and the concrete structure and parameters are described in Ref. [20]. For the frequencies between the ranges [6.81, 8.26] GHz and [12.72, 15.21] GHz, μ _x and μ _y are negative respectively.

In Fig. 1, the reflectances for linearly polarized wave along the x direction and y direction are shown each as a function of the frequency for three different thickness values of the anisotropic metamaterial plate. There is a resonant peak of the reflectance appearing near the magnetic resonant frequency. For the x- (y-)polarized wave, the resonant peak of the reflectance R_x (R_y) occurs near the resonant frequency of μ _y (μ _x). With the increase of the thickness of the plate, the resonant gap appears near the resonant frequency. This phenomenon is unusual because the multilayer system necessarily exhibits band gap structure for the conventional material.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Reflectances Rx (a) and Ry (b) each as a function of frequency for different thickness values of the anisotropic metamaterial. The solid lines, dashed lines, and dotted lines correspond to the metamaterials with the thickness l = 0.005 m, 0.01 m, and 0.05 m respectively.

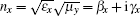
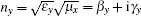
In order to understand this phenomenon, we plot the real parts of the refractive index and in Fig. 2. We can find that β _x (β _y) is zero near the resonant frequency f = 6.80 GHz (f = 12.71 GHz). This gap is similar to the zero averaged refractive index gap of the layered ordinary and negative refractive index material.^[14]

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Real parts of the refractive index of the anisotropic metamaterial.

Since the propagation property of the metamaterial is dependent mainly on refractive index and , we could expect resonant peak of the reflectance if the permittivity is in the form similar to anisotropic permeability in Eq. (31). We consider the metamaterial slab characterized by

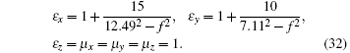
The calculated results for reflectances R_x and R_y are shown in Figs. 3(a) and 3(b). We could see that the resonant peak of the reflectance can also appear if the permittivity is anisotropic.

Fig. 3.

	Figure Option ViewDownloadNew Window
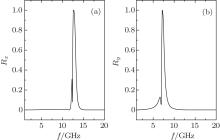	Fig. 3. Reflectances Rx (a) and Ry (b) each as a function of frequency for the anisotropic metamaterial (thickness l = 0.01 m) with just anisotropic permittivity.

Next, we proceed to the case in which both the permittivity and permeability are anisotropic, i.e., the metamaterial slab is characterized by and given by Eqs. (31) and (32) respectively. The calculated results for reflectances R_x and R_y are given in Figs. 4(a) and 4(b). The results show that both the reflectance R_x and the reflectance R_y have two resonant peaks which are located near the electric resonant frequency and the magnetic resonant frequency, respectively. This is sensible because the permittivity and permeability together determine the propagation of the quantized radiation.

Fig. 4.

	Figure Option ViewDownloadNew Window
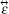
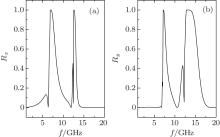	Fig. 4. Reflectances Rx (a) and Ry (b) each as a function of frequency for the anisotropic metamaterial (thickness l = 0.01 m) with both permittivity and permeability as anisotropic tensors.

Finally, the effect of the absorption is considered. To study the effect due to the absorption, we introduce an imaginary part into the permeability. For the metamaterial with absorption, the permittivity and the real part of the permeability are taken also as Eq. (31) and the imaginary parts are taken as . The thickness of the metamaterials slab is set as l = 0.01 m. The calculated results for reflectances R_x and R_y are shown in Figs. 5(a) and 5(b) by dashed lines. In order to make a comparison, the corresponding results without absorption are also plotted by solid lines. It is clear that the reflection feature does not change with the introduction of the absorption, although the reflectance decreases a little near the resonant frequency which is caused by the absorption of the metamaterial.

Fig. 5.

	Figure Option ViewDownloadNew Window
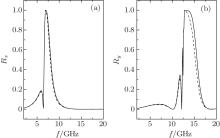	Fig. 5. Reflectances Rx (a) and Ry (b) each as a function of frequency for the anisotropic metamaterial slab (thickness l = 0.01 m) with (dashed lines) and without (solid lines) absorption. For metamaterial with absorption, the permittivity and the real parts of the permeability are taken as Eq. (31) and the imaginary part as .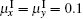

The phenomenological quantization of the electromagnetic field in dispersive and absorptive anisotropic magnetodielectric metamaterial is performed. Input– output relations of quantized radiation are derived for a single layer structure with the anisotropic metamaterial using the Green-function approach. According to these relations we calculate the reflectance for the linearly polarized radiation through such a structure. The results show that the resonant peaks of reflectance for different polarized waves occur at the corresponding resonant frequencies of the permeability and permittivity. This indicates an application of the anisotropic metamaterial to the reflector for a certain polarized wave. Furthermore the single slab structure can realize the resonant gap which is corresponding to the zero averaged gap realized by the multilayer structure with conventional material and negative refractive index material. Finally the effects of the absorption are considered and the results show that the above properties do not change with the introduction of the absorption. Unlike previous work in Ref. [9], our work introduces the noise magnetization operator, so our method can be applied to the propagation of quantized wave in anisotropic metamaterial with arbitrary permittivity and permeability tensors. We should point out that all our calculations are performed for single layer structure. The extension to the multilayer system is straightforward. It can be done step by step in essentially the same way as that for the single layer structure.