†Corresponding author. E-mail: haihua@jlu.edu.cn
*Project supported by the National Basic Research Program of China (Grant No. 2011CB921603), the National Natural Science Foundation of China (Grant Nos. 11374126, 11347137, 11404336, and 11204103), the China Postdoctoral Science Foundation (Grant No. 2013T60317), and the National Fund for Fostering Talents of Basic Science, China (Grant No. J1103202).
We experimentally demonstrate multiple frequency conversion via atomic spin coherence of storing a light pulse in a doped solid. The essence of this multiple frequency conversion is four-wave mixing based on stored atomic spin coherence. Through electromagnetically induced transparency, an input probe pulse is stored into atomic spin coherence by modulating the intensity of the control field. By using two different control fields to interact with the coherently prepared medium, the stored atomic spin coherence can be transformed into three different information channels. Multiple frequency conversion is implemented efficiently by manipulating the spectra of the control fields to scatter atomic spin coherence. This multiple frequency conversion is expected to have potential applications in information processing and communication network.
For further quantum information processing, it is necessary to have some independent devices such as quantum memory, quantum repeater, and quantum routing, where quantum information can be exchanged between the light field and experimental medium in a controlled manner. Photons are efficient and robust information carriers due to their weak interaction with the environment, but it is difficult to manipulate them. Recent research shows that electromagnetically induced transparency is a promising technique to manipulate the light field.[1] Electromagnetically induced transparency (EIT) makes the probe light pass though an opaque medium without absorption in the case that an additional control field is used to produce quantum interference. In particular, light storage based on EIT has aroused significant interest due to the applications in both classical and quantum information processing.[2– 6] EIT-based light storage is explained in terms of a dark-state polariton, which can interconvert from a light component to an atomic spin coherence component by manipulating the Rabi frequency of the control field.
As is well known, an EIT-driven medium is also used to enhance nonlinear optical interaction, which is very useful for frequency conversion, such as to enhance four-wave mixing (FWM).[1] Recently, researchers have been interested in using atomic nonlinearities to enhance light storage, or using light storage to enhance optical nonlinearities. Large cross-Kerr nonlinearities have been achieved by using light storage.[7] Optical nonlinearities have been used to improve the readout in light storage.[8] The selective retrieval of the stored light has been realized by applying a new read control field.[9– 12] Using a combination of EIT and FWM, the storage of the input probe and generated idler light have been studied in atomic gases.[13, 14]
The experimental mediums used for demonstrating the EIT and the associated effect are almost exclusively atomic gases. One of the difficulties in using atomic gases for the demonstration is the diffusion effect caused by atomic motion. For practical applications, solid-state mediums can be considered as an alternative to atomic gases. They provide spatially fixed interaction centers, and do not suffer atomic diffusion. Recently, rare-earth-doped solids have received considerable attention in information processing.[15] They exhibit advantageous spectrum properties of small homogenous broadening and long spin coherence time, which allows for the efficient buildup of atomic coherence.[16] Some physical phenomena related to EIT effect have been performed experimentally by using doped solids.[17– 22]
In the present work, we experimentally investigate the multiple frequency conversion via atomic spin coherence by EIT-based light storage in a Pr3+ :Y2SiO5 (Pr:YSO) crystal. The essence of this multiple frequency conversion is four-wave mixing based on stored atomic spin coherence. Under dynamical EIT, an input weak probe pulse is stored into atomic spin coherence between two ground states. By using two control fields to interact with the coherently prepared medium, the stored atomic spin coherence is transformed into three different information channels. The performance of multiple frequency conversion relies on the number and frequencies of the control fields scattering the stored atomic spin coherence. Three output signals can be selectively obtained by manipulating the spectra of the retrieval control fields. The generation processes of three output signals are further discussed, and correspond to three different physical processes. This multiple frequency conversion in solid-state medium is important for light signal transfer and propagation. It allows us to manipulate coherently the behavior of the light field in a controlled manner, and find its applications in information processing and communication network.
The experimental demonstrations are performed in the transition of 3H4 → 1D2 of the Pr:YSO crystal as shown in Fig. 1(a). The wavelength of the optical transition is 605.977 nm. The inhomogeneous broadening of the transition of 3H4 → 1D2 is about 6 GHz, and its homogeneous broadening is several MHZ. The spin inhomogeneous broadening of the transition of 10.2 MHz is about 30 kHz. Single ensembles of Pr ions can be prepared by the technique of spectral hole-burning.[15] The ground state (3H4) and the excited state (1D2) each have three degenerate hyperfine states. The EIT lambda system consists of two lower levels (| 1〉 and | 2〉 ) and an upper level (| 3〉 ). The control field ω c1 couples the transition of | 1〉 → | 3〉 , and the probe signal ω p1 couples the transition of | 2〉 → | 3〉 . The repump field ω r couples the transition of 3H4 (± 5/2) → 1D2 (± 5/2), and is used to pump the populations on the levels | 1〉 and | 2〉 . The crystal is coherently prepared by storing the probe signal ω p1 into atomic spin coherence. An additional control field ω c2 is used to scatter stored atomic spin coherence to perform the frequency conversion. The control field ω c2 selectively drives the transitions of | 1〉 → | 4〉 and | 2〉 → | 3〉 , which depends on the chosen frequency of the ω c2 field. The ω p2 and ω p3 fields are newly-generated FWM signals when the control field ω c2 drives the transitions of | 1〉 → | 4〉 and | 2〉 → | 3〉 , respectively. For simplicity, ω p1, ω p2, ω p3, ω c1, and ω c2 are denoted by P1, P2, P3, C1, and C2 in the figures, respectively.
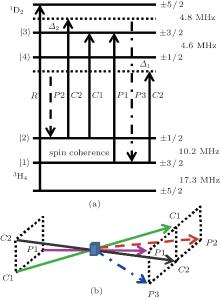 | Fig. 1. (a) Level coupling scheme of Pr ions, and (b) experimental schematic diagram of the frequency conversion. |
The experimental schematic diagram is shown in Fig. 1(b), which is similar to that in Ref. [11]. Coherent-899 laser is used as the initial light source. The laser output is further divided into the required laser beams by beam splitters. Each laser beam is guided to an acousto– optic modulator (AOM), by which the frequency and pulse sequence of laser beams can be controlled independently. To match the level coupling of Fig. 1(a), the ω p1, ω c1, and ω r fields are upshifted by 210.2 MHz, 200 MHz, and 232.3 MHz from the initial laser frequency, respectively. In order to drive different optical transitions, the control field ω c2 can have various frequencies by controlling the driver of AOM. The generations of the ω p2 and ω p3 signals satisfy the phase-matching conditions Kp2 = Kc2 − Kp1 + Kc1 and Kp3 = Kc2 + Kp1 − Kc1, respectively. Through the lens, all laser beams are focused into the crystal at a small angle. The noncollinear configuration efficiently reduces the noise from the scattering of the control fields. The dopant concentration of Pr:YSO is 0.05%, and the length of this crystal is 3 mm. The crystal is placed inside a cryostat with a temperature of 3.5 K. The probe signals passing through the crystal are detected by photodiodes connected to a fast oscilloscope. The powers of ω p1, ω c1, ω c2, and ω r are 0.3 mW, 5 mW, 5 mW, and 1 mW, respectively, and are kept constant. We change the number and frequency of the retrieval control fields to obtain multiple frequency conversion.
To prepare the populations on level | 1〉 , the control and repump pulses (ω c1 and ω r) are first used and last for 5 ms. Subsequently, the control pulse ω c1 resonant with the transition of | 2〉 → | 3〉 and the probe pulse ω p1 resonant with the transition of | 1〉 → | 3〉 are used to demonstrate light storage as shown in Fig. 2. Due to the steep dispersion induced by EIT, the group velocity of probe pulse ω p1 slows down. When the control field ω c1 is switched off, the probe signal ω p1 is stored into atomic spin coherence between levels | 1〉 and | 2〉 . The generated atomic spin coherence inherits the coherent information of the probe signal ω p1. After a given storage time, by switching back on the control field ω c1, the stored atomic spin coherence is converted into the probe signal ω p1. The storage and retrieval of the light pulse correspond to the buildup and depletion of atomic spin coherence, respectively, where the populations are coherently transferred between levels | 1〉 and | 2〉 due to stimulated photons exchanging between ω c1 field and ω p1 signal. Such storage and retrieval process can be understood as time-delayed FWM, and the retrieved probe pulse ω p1 is considered as an FWM signal, which is generated by using the read control field ω c1 to scatter stored atomic spin coherence.
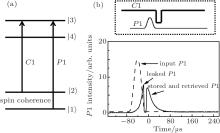 | Fig. 2. (a) Energy level coupling of EIT-based light storage, and (b) experimental results of the storage and retrieval of the probe signal ω p1. |
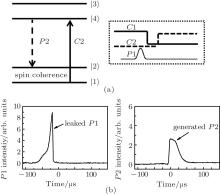
As is well known, a coherently prepared medium can be used to enhance optical nonlinearities. By using atomic spin coherence prepared by EIT-based light storage, efficient frequency conversion can be performed. For experimental demonstrations, instead of the control field ω c1, an additional control field ω c2 is used to scatter stored atomic spin coherence. By using AOM, the frequency of the ω c2 field is upshifted by 205.6 MHz from the initial laser frequency. In this case, the ω c2 field is resonant with the transition of | 1〉 → | 4〉 . The pulse sequences of this demonstration are shown in Fig. 3(a). After switching off the ω c1 field, the ω c2 field is applied to the coherently prepared crystal. Due to the interaction between the control field ω c2 and atomic spin coherence, an efficient FWM signal ω p2 is obtained as shown in Fig. 3(b). The ω p2 signal is emitted in the transition of | 4〉 → | 2〉 under two-photon resonance. In this frequency conversion, the photons of the ω c2 field are coherently converted into the photons of the ω p2 signal through stimulated emission. The generation of the ω p2 signal satisfies two-photon resonance and phase-matching condition of Kp2 = Kc2 − Kp1 + Kc1 as shown in Fig. 1(b), thus the newly-generated ω p2 has a new frequency and a new propagation direction. Because no ω c1 field is applied, there is no output signal in the ω p1 channel. The generation of the ω p2 signal can be understood by the amplification of spontaneous Raman scattering due to the advanced preparation of atomic spin coherence.[14, 23]
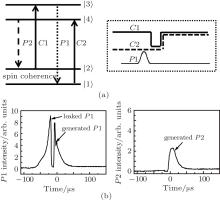
In the next demonstration, we simultaneously apply two control fields (ω c1 and ω c2) to the crystal after the buildup of atomic spin coherence as shown in Fig. 4(a). The frequency of the ω c2 field is still kept at upshifted 205.6 MHz from the initial laser frequency, and resonant with the transition of | 1〉 → | 4〉 . Due to the interaction between two control fields and atomic spin coherence, two probe signals (ω p1 and ω p2) are simultaneously obtained, which correspond to two FWM processes as shown in Fig. 4(b). These two FWM processes both deplete stored atomic spin coherence, but correspond to different level couplings and stimulated photons exchange processes. The ω p1 signal is emitted in the transition of | 3〉 → | 1〉 and the ω p2 signal is emitted in the transition of | 4〉 → | 2〉 . For the generation of the ω p2 signal, the photons of the ω c2 field are coherently converted into the photons of the ω p2 signal. For the generation of the ω p1 signal, the photons of the ω c1 field are coherently converted into the photons of the ω p1 signal. Each generated signal satisfies its own phase-matching condition, thus the ω p1 signal remain the initial frequency and propagation direction, and the ω p2 signal has a new frequency and propagation.
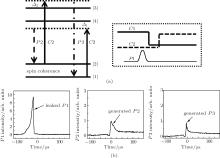
By changing the frequency of the control field ω c2, we find that the ω c2 field can simultaneously drive two optical transitions, and two FWM signals are obtained by using only one control field ω c2. To perform this demonstration, the frequency of the ω c2 field is upshifted by 203.5 MHz from the initial laser frequency. Under this chosen frequency, the ω c2 field couples | 1〉 → | 4〉 transition with the detuning of 2.1 MHz and also couples | 2〉 → | 3〉 transition with the detuning of 3.5 MHz as shown in Fig. 5(a). By applying this ω c2 field with a frequency of upshifted 203.5 MHz to the coherently prepared crystal, the stored atomic spin coherence is converted into two FWM signals (ω p2 and ω p3) as shown in Fig. 5(b). These two FWM processes deplete the same atomic spin coherence, but have different coupling levels and phase-matching conditions. For the case of the ω c2 field coupling the transition of | 1〉 → | 4〉 , the generation of the ω p2 signal satisfies the phase-matching condition of Kp2 = Kc2 − Kp1 + Kc1, where the photons of the ω c2 field are coherently converted into the photons of the ω p2 field through stimulated emission. For the case of the ω c2 field coupling the transition of | 2〉 → | 3〉 , the generation of the ω p3 signal satisfies the phase-matching condition of Kp3 = Kc2 + Kp1 − Kc1 as shown in Fig. 1(b), where the photons of the ω c2 field are coherently converted into the photons of the ω p3 field through opposite stimulated emission. The generation of the ω p3 signal corresponds to the selective retrieval of the stored light as reported in previous research.[9– 12] Due to two-photon resonance and phase-matching condition, each frequency conversion signal (ω p2 and ω p3) has a new frequency and propagation direction from the input ω p1 signal.
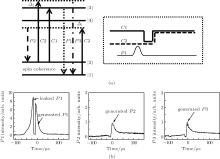
In the case that the frequency of the control field ω c2 is fixed at upshifted 203.5 MHz, the stored atomic spin coherence is converted into three output signals (ω p1, ω p2, and ω p3) when two control fields (ω c1 and ω c2) are simultaneously applied to the coherently prepared crystal as shown in Fig. 6. Three output signals have different frequencies and propagation directions. The ω p1 signal corresponds to the retrieval of the stored light. The ω p2 signal corresponds to the amplification of spontaneous Raman scattering. The ω p3 signal corresponds to the selective retrieval of the stored light. The ω p1 signal comes from the interaction between the ω c1 field and stored atomic spin coherence. The ω p2 and ω p3 signals come from the interaction between the ω c2 field and stored atomic spin coherence. For the generation of the ω p1 and ω p3 signals, the populations of level | 2〉 are transferred to level | 1〉 through stimulated emission. However, the population transfer process is opposite for the generation of the ω p2 signal. Although one initial probe field (ω p1) is stored into atomic spin coherence, we can obtain three output signals by using two control fields. Thus, multiple frequency conversion can be realized by the above experimental operation.
We have experimentally demonstrated multiple frequency conversion via atomic spin coherence prepared by light storage in a doped solid. Under dynamic EIT, the input probe pulse is stored into atomic spin coherence between two ground states. By applying two different control fields to the coherently prepared crystal, the stored atomic spin coherence is converted into three different output signals. The generation processes of the output signals are further discussed. The performance of multiple frequency conversion depends on the spectrum of the control fields scattering atomic spin coherence. The essence of this multiple frequency conversion is four-wave mixing based on stored atomic spin coherence. Such a multiple frequency conversion allows manipulating the light signal in a coherent and all-optical manner, and will be important in further information processing and communication network.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|