†Corresponding author. E-mail: krasn@icm.krasn.ru
Conditions have been studied under which a polychromatic optical superlattice can form and trap the Coulomb cluster of two strongly interacting ions. In our previous work (Krasnov I V and Kamenshchikov L P 2014 Opt. Comm.312 192) this new all-optical method of obtaining and confining the Coulomb clusters was demonstrated by numerical simulations for special values of the optical superlattice parameters and in the case of Yb ions. In the present paper the conditions are explicitly formulated, under which the long-lived two-ion cluster in the superlattice cell is formed. The peculiarity of these conditions is the renormalization of the ion–ion Coulomb interaction. Notably, the renormalized Coulomb force is determined by the effective charge which depends on the light field parameters and can strongly differ from the “bare” ion charge. This result can be accounted for by the combined manifestation of the quantum fluctuations of optical forces, nonlinear dependence of these forces on the velocity, and non-Maxwellian (Tsallis type) velocity distribution of the ions in the optical superlattice. Explicit analytical formulas are also obtained for the parameters of the optical two-ion cluster.
The capability of laser radiation to control the translational degrees of freedom has intensively been studied for several decades. These studies offer a wide spectrum of important applications and useful theoretical models.[1, 2] The mechanical action of light is used for the deep laser cooling of both neutral atoms and charged atomic ions as well as for the trapping of neutral atoms. Electromagnetic traps (similar to the Paul or Penning traps) are conventionally used for the ion confinement.
Recently the interest has arisen from the problem of all-optical trapping of ions, i.e., from ion trapping without applying radiofrequency or electrostatic and magnetostatic fields.[3, 4] Unfortunately, the shallow depth Δ Wd of monochromatic dipole trap (ODT) or optical lattice (OL) can be a serious obstacle for their use in the trapping of a few ions due to the Coulomb repulsion of ions (although ODT and OL are quite successfully used for all-optical trapping of neutral atoms[2, 5– 7]).
An alternative method for long-time trapping of the interacting ions, the confinement of the ions in a three-dimensional (3D) dissipative polychromatic optical superlattice (OSL), [8, 9] was considered in Ref. [4]. The action of such a 3D OSL (with the spatial period ∼ L greatly exceeding the light wavelength λ , L ≫ λ ) on the ions is based on the effect of the gradient (dipole) force rectification in the non-monochromatic (bichromatic, polychromatic) optical fields.[10– 12] Due to unique features of the rectified gradient force RcGF, [10] OSL is capable of inducing 3D superdeep (as compared with ODT or OL) potential wells (for the ions) with the value of depth
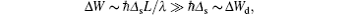
where ħ Δ s is the characteristic value of the light (Stark) shifts of ionic levels. Moreover, the light-induced friction force is exerted on the ions in OSL, resulting in the cooling of ions. The computer simulation results of the ion motion in OSL (for the case of two ytterbium ions) presented in Ref. [4] demonstrate that the OSL action on the ions can lead to their deep cooling and to the formation and long-time confinement of the two-ion (Coulomb) cluster. Such a cluster has an approximately fixed (with the accuracy up to small fluctuations) interionic distance (size) and the center-of-mass (CM) position. Note that in the considered two-ion system all the main factors hindering the all-optical ion trapping are present: the Coulomb repulsion, quantum fluctuations of the optical forces, [1, 13] and finite depth of the light-induced potential wells.
The analysis of the computer simulation results allows one to formulate the following conditions for the long-lived two-ion cluster formation within a single unit cell Ω 0 of OSL.[4]
There must exist equilibrium points {η * } in the six-dimensional configuration space (of the ion spatial positions {η } = (r1, r2)), where the Coulomb repulsion of ions is balanced by the trapping force (RcGF F0R in our model) and the total potential energy Ut({η }) achieves a local minimum, i.e., a point where
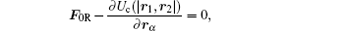
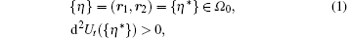
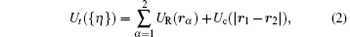
where α = 1, 2, rα is the position of the α -th ion, UR is the potential of RcGF, Uc(r) = e2/4π ε 0r is the Coulomb energy of two ions separated by the distance r, e is the ion charge, d2Ut({η * }) is the second differential of Ut({η }) at the point {η * }.
There exist equilibrium cluster configurations {η * } if the value of the light-induced potential well depth Δ W is sufficiently large as compared with the Coulomb energy Uc(L):[4]
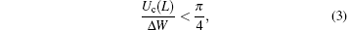
where L is the spatial period of OSL.
The cluster configuration {η * } is metastable[4] due to the quantum fluctuation of the optical trapping force. Notably, the metastable-state lifetime τ M is a strongly increasing function of the ratio of the potential well depth Δ W to the effective cluster temperature T, which is established by the balance between the optical cooling of the ions and their heating due to the optical force fluctuations. Therefore, another important condition for the formation of the long-lived cluster in OSL can be presented by the inequality
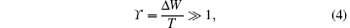
where T is expressed in energy units. Inequality (4) also provides the smallness of the random fluctuations of the interionic distances (at the time points t < τ M).[4]
The presented conditions seem perfectly natural and simple for the interpretation. However they are valid only in the approximation of slow ions (SI), i.e., in the case of

where 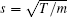
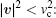
The present paper considers a new model where the parameter ε is not small enough and an explicit velocity dependence of RcGF, friction and diffusion coefficients are taken into account.
The necessity for the special analysis of this model is due to the following important circumstances. The low (sub-Doppler) limit of the ionic temperature in OSL is achieved at the low intensity of the optical field and is accompanied by the violation of condition (5).[9] The velocity profile of RcGF is determined (see e.g. Refs. [10], [12], and [14]) by the multipliers of the ℒ (vj/vc) type, where vj are the velocity projections onto the axis j ∈ {x, y, z}, and ℒ (u) is the Lorentzian function:
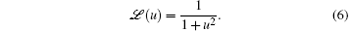
Therefore, RcGF is a non-conservative force, and equation (1) and condition (2) (as well as the outcoming relation (3)) loose their senses at ε ∼ 1 and do not allow one to unambiguously predict possible equilibrium configurations of the two-ion cluster. The metastability condition (4) is also difficult to explain since it is not understandable in advance how to determine accurately the height of the energy barrier preventing the cluster from decaying in the case of the non-conservative RcGF.
Finally, a reasonable question arises. Is it at all possible in this case (i.e., at ε ∼ 1) to form in OSL a long-lived Coulomb ion cluster which is similar to that predicted by the computer simulation in Ref. [4].
Our answer to this question of principle is “ yes” , and a correct formulation of the basic conditions for the formation of such a cluster in OSL is given. These conditions (with an arbitrary value of ε ) can be written in the form analogous to relations (1)– (4), where it is, however, necessary to perform suitable renormalization (re-definition) of the parameters and forces. In particular, for renormalization of the Coulomb interaction it is necessary to replace the charge e (in the expression for Uc(r)) by the effective (renormalized) charge e* :

where e* is the function of the governing parameters of OSL, χ , and G.[9]
In other words, one shows that with the arbitrary value of the parameter ε and the time scales larger than the inverse friction coefficient ϰ − 1, the light-induced Brownian motion of the ions in the configuration space {η } can be described using a renormalized SI model.
Our analysis is based on the asymptotic expansion of the Wigner distribution function (for the ions in OSL) in the Knudsen number of problem[9]

where λ r ∼ sϰ − 1 has the meaning of the effective free-path length of the ions in a viscous “ fluid” of photons.
Another interesting aspect (not only for optical physics but also for statistical mechanics (e.g., see Ref. [15]) of the problem under consideration is connected with the non-Maxwellian characteristic of the velocity distribution of ions in OSL. It is shown that the main part of the velocity distribution can be well approximated by the 3D Tsallis distribution
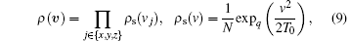
where expq(v2) = [1 + (q − 1)v2]1/1− q is the so-called q-Gaussian, normalizing factor N, and the index q and T0 each are a function of the governing parameters of OSL.
We consider two identical ions with the tripod configuration of the energy levels (Fig. 1) located in the 3D polychromatic OSL[8, 9] and assume that the light field drives the closed dipole transition | Fb = 1, Mb ∈ {− 1, 0, 1}〉 → | Fa = 0, Ma = 0〉 where Fα and Mα are the full angular momenta and their projections for the ground (α = b) and excited (α = a) internal ionic states, respectively. The light field (with a complex amplitude E) forming OSL is a superposition of three color coherent fields and a partially coherent (fluctuating) resonant field Eʹ with the bandwidth Γ :
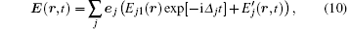
where ej denotes the unit basis vectors of the Cartesian coordinate system, j ∈ {x, y, z}, Δ j are the detunings from the resonant frequency ω 0, which are subject to the conditions
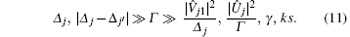
Here, 
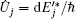

In the Cartezian representation, i.e., in the representation of the basis wave functions (of the intra-ionic motions) for the excited | a〉 and ground | bj〉 states (where j ∈ {x, y, z}), in which the matrix elements of the dipole moment d̂ are directed along the unit vectors ej (j ∈ {x, y, z}),
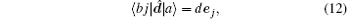
the effective Hamiltoninan Ĥ eff (in the interaction picture) describing the interaction of a single ion with the light field has the form[9]
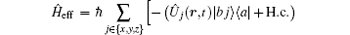
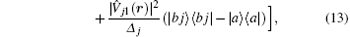
where the terms ∝ | V̂ j1(r)| 2/Δ j = Δ sj(r) and − ∑ | V̂ j1(r)| 2/Δ j = Δ s(r) describe the Stark shifts of the atomic levels induced by the “ far-off-resonant” field E1.
The particular configurations of the fields Ej1(r) and 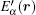
The interference of different wave components of each “ far-off-resonant” field Ej1(j ∈ {x, y, z}) leads to the spatial modulation of the light (Stark) shifts along the i axis
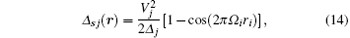
where (ji) is the ordered pair of indices (e.g., i = y for j = x; i = x for j = z; i = z for j = y), ri = (rei), Ω i ∼ 2/λ is the frequency of the spatial modulation along the i axis, vj(j ∈ {x, y, z}) are the amplitudes of the local Rabi frequencies V̂ j1(r). Then, taking Eq. (13) into account, one can see that ħ Δ sj(ri) and − ∑ jħ Δ sj(ri) are the potentials experienced by the ion in the states | bj〉 , j ∈ {x, y, z} and | a〉 , respectively.
The partially coherent fields 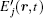

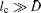
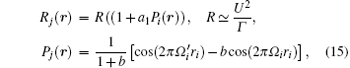
where U is the amplitude of the local Rabi frequencies Û j(r, t), a1 and b are the independent parameters determined by the amplitudes of interfering wave components of the field 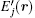
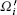

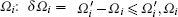
So the resonant field E′ induces the spatial modulation of the ionic state populations (due to the modulation of the transition rates Rj(r)) and the “ far-off-resonant” fields Ej1ej induce the effective potentials (∝ Δ sj(r), Δ s(r)), which determine the ion motion depending on its internal state. As a result, OSL is formed.[8, 9] Figure 1 illustrates the general physical picture of the OSL action on the particles with tripod configuration of levels. The OSL periods Li(i ∈ {x, y, z}) are determined by the spatial beat frequencies, Li = (1/δ Ω i) ≫ λ . These three spatial periods Lx, Ly, and Lz can be controlled independently by changing the OSL angular detunings.[8, 9]
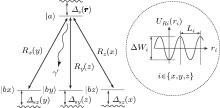 | Fig. 1. Schematic picture of the OSL action on tripod-type particles. | a〉 and | bj〉 (j ∈ {x, y, z}) are the internal ionic states in the representation, in which the matrix elements of the dipole moments 〈 bj| d̂ | a〉 are directed along the Cartesian axes (See Eq. (12)); Δ sj(ri) and Δ s(r) are the light shifts of the states | bj〉 and | a〉 , (ji) ∈ {(xy), (yz), (zx)}; Rj(ri) are the rates of incoherent transitions | bj〉 → | a〉 . The spatial frequencies Ω i, 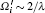 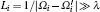 |
Apart from the periods Li, the most important governing parameters of OSL are the parameters determined by the intensity values of the fields (j ∈ {x, y, z})
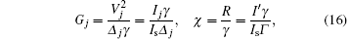
where Ij is the intensity of the waves forming the “ far-off-resonant” field ∝ Ej1ej, I′ is the intensity of the partially-coherent field E′ , Is = ħ ω 0k2γ /6π is the intensity of the optical radiation saturating the quantum transition. These parameters determine the values of the optical forces.
Further, we restrict ourselves to the most interesting case
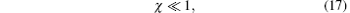
i.e., to the case of the weak field E′ , when sub-Doppler cooling of ions becomes possible.[9]
In order to simplify the notations and calculations, it is also assumed that the parameter b ≫ 1 (i.e., the term ∝ cos(2π Ω ri) dominates in Eq. (15)) and all the parameters Gj (in Eq. (16)) are equal: Gi = G > 0 for i ∈ {x, y, z} (i.e., Ij/Δ j = Ij′ /Δ j′ , for ∀ j ≠ j′ ). Besides, it is assumed that the “ far-off-resonant field” E1 is not too strong and G ⪅ 1/2.
Our study is based on the quantum kinetic equation for the two-particle Wigner phase-space distibution function f̆ (r1, υ 1, r2, υ 2, t) which describes the ion motion in OSL.
We introduce the dimensionless quantities by measuring positions in units of Lx = L, time in units of 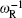
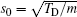
Then, FPE for the distribution function (DF) averaged over the spatial micro-oscillations, f = 〈 f̆ 〉 s, can be written as follows (in the case of a moderate spatial modulation of Rj(r), 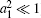
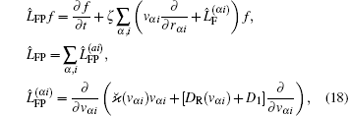
where α ∈ {1, 2}, i ∈ {x, y, z}, vα i = (vα ei), rα i = (rα ei), ζ = s0/ω RL is the parameter determining the scale of the Knudsen number value (see Eq. (8)), ζ ∼ Kn, and the friction and diffusion coefficients 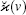

with 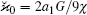
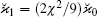
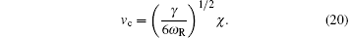
The operators 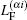

where
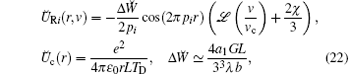
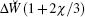
The first term on the right-hand side of Eq. (21) is associated with RcGF and the second term is related to the repulsion Coulomb force.
Note, that we retain (in the expressions for coefficients) small (at χ ≪ 1) but velocity-independent terms since they (to be seen later) determine the very far tails of DF (i.e., DF at vα ≫ vc).
Equation (18) is the generalization of FPE (for the particles in OSL) presented in Ref. [9]. This equation takes into account the rectified radiation force dependence on the ion velocity and the ion– ion Coulomb interaction. Here, the situation is considered, where the characteristic frequency of the ionic translational motion induced by the Coulomb interaction is considerably lower than the decay rate γ ′ of the excited state | a〉 and the rate R of the transitions | ja〉 − | b〉 (in practice, this is provided by the smallness of the parameters ω R/γ , ω R/R). Therefore, the ion– ion Coulomb interaction does not influence the process of the optical force formation. Then, the expressions for the RcGF, friction, and diffusion coefficients can be derived in the framework of the one-particle model by using the standard techniques of the quasi-classical kinetic theory of the light pressure force[1, 17, 18] and the kinetic theory of rectified radiation forces.[9, 14]
FPE (18) is equivalent to the following system of stochastic differential equations in the Stratonovich sense[19]
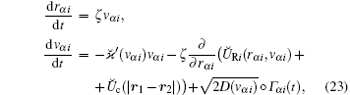
where α ∈ {1, 2}, i ∈ {x, y, z}, D(v) = DR(v) + D1, 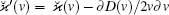
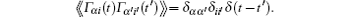
Thus, equation (23) describes the light-induced (Brownian) motion of ions in the 12-dimensional phase space (r1, r2, υ 1, υ 2). A significant difference from the model in Ref. [4] is due to the multiplicative characteristic of noises since the coefficients D(vα j) in Eq. (23) depend on the particle velocity. Within the range 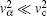
In this section the equations of the ion motion in the configuration space {η } = (r1, r2) are derived. These equations are to be used further to obtain correct conditions for the formation of the metastable two-ion (Coulomb) cluster in OSL when inequality (5) is violated. The overdamped characteristic of the ion motion in OSL, which is expressed by inequality (8), Kn ∝ ζ ≪ 1, allows using the method of Chapman– Enskog type (e.g., see Refs. [20] and [21]) for finding the solution of Eq. (18) on a diffusion time scale 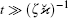
Introduce the “ slow” time τ = ζ 2t and the operators
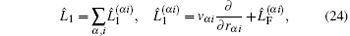
and rewrite Eq. (18) as
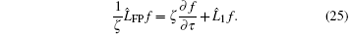
In the manner of the Chapman– Enskog method we implement the following asymptotic expansion of f and of the time derivative in the parameter ζ :
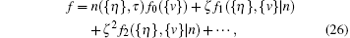
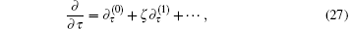
where {v} = (υ 1, υ 2), n is the two-particle space distribution function,
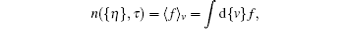
the functions fm depend on time τ as a functional of n({η }, τ ) and should satisfy the condition 〈 fm〉 v = 0. Substituting Eq. (26) into Eq. (25), one obtains a chain of equations:

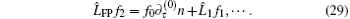
Then, the expansion of the probability density currents Jα = 〈 fυ α 〉 v (α ∈ {x, y, z}) has the form
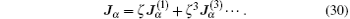
Here, we take into account that 〈 f0υ α 〉 v = 〈 f2υ α 〉 v = 0.
Intergrating Eq. (25) over the velocity space {v} and taking Eq. (30) into account, we obtain a two-particle continuity equation for n({η }, t)
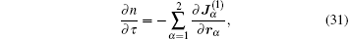
where the correction term of the order O(ζ 2) is ignored. It is important that equation (31) is the solvability condition for Eq. (29). So, the explicit form of the continuity (Eq. (31)) can be obtained with the solution of Eqs. (28).
The solution of Eq. (28) for f0({v}) can be presented as the product of the q-Gaussian (Tsallis) distribution and Gaussian distribution functions

where ρ s(v) is given by Eq. (9), 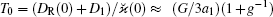
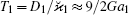
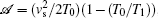
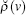
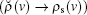

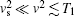
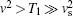

The indicated peculiarities of the distribution function allow calculating the zeroth, second, and fourth moments of the 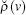
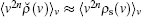
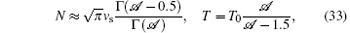
where Γ (𝒜 ) is the gamma function. The estimate for the lowest ion cooling limit: 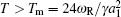
Also note that T ≈ T0 at 𝒜 ≫ 3/2, i.e., at large 𝒜 the kinetic temperature T tends to the value T0 corresponding to the SI model (where the velocity profile of the radiation forces is not taken into account).[4]
Further, the solution of Eq. (28) for f1 is (at χ 1 ≪ 1):
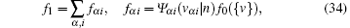
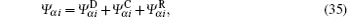
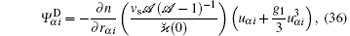
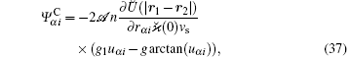
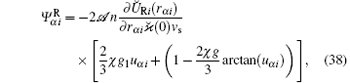
where uα i = vα i/vs, 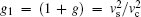
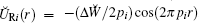
From expressions (35)– (38) it follows that ζ f1 is the small correction to f0 at 
One can also see that the perturbations of 
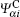
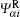
Using expression (34) to calculate the probability density currents, 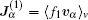
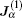


where the effective potentials and the temperature Teff are introduced. They are determined by the relations:
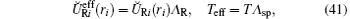

with r12 = | r1 − r2| and corrective multipliers depending on the governing parameters of OSL:

The effective temperature Teff is determined so that the effective temperature, friction, and spatial diffusion coefficients (i.e., Teff, 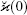
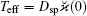
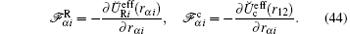
Using the effective forces one can express the density currents 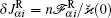
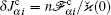
Equation (39) is equivalent to the following system of stochastic differential equations (reduced Langevin equations):
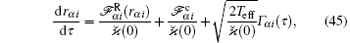
where α ∈ {1, 2}, i ∈ {x, y, z}. Equation (45) is considerably simpler for the analysis than Eq. (23) since it is a system of six stochastic differential equations with additive noises, while equation (23) is a system of twelve stochastic differential equations with multiplicative noises.
On the other hand, it is possible to introduce a renormalized version of the model based on Eq. (23) by means of the following substitutions:
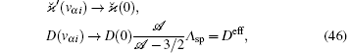
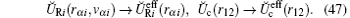
This renormalized model formally corresponds to the SI approximation (since 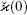

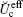
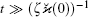
How this renormalization (and, consequently, the factor of nonlinear velocity dependence of optical forces) influences the formation conditions of the two-ion (Coulomb) cluster in OSL, is considered in the following section.
Taking into account the results of the previous section it is possible to reformulate the formation conditions of the two-ion (Coulomb) cluster in OSL (see Eqs. (1)– (4)) by substituting the “ bare” Coulomb force and RcGF by the renormalized forces. The influence of this renormalization appears to be rather significant for the OSL parameters which correspond to the minimum ion temperatures (see Subsection 3.2): 𝒜 ∼ 3, g ≫ 1. Indeed, the effect of renormalization can be ignored if the corrective multipliers Λ c and Λ sp are close to unity: Λ c ≈ 1 and Λ sp ≈ 1, i.e., when
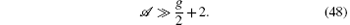
Note that this condition is equivalent to inequality (5).
Inequality (48) imposes rather strong constraints on the governing parameters G and χ and is unlikely to be satisfied at 𝒜 ∼ 3. Figure 2 illustrates the dependence of the renormalized charge e* on the parameter G for the case of the 171Yb+ ions (γ = 4.81 × 107 s− 1, λ = 370 nm). One can see from Fig. 2 that the effective charge e* can exceed the “ bare” charge by more than 1.5 times and, consequently, the effective Coulomb force ∝ (e* )2 can increase several times in comparison with the “ bare” Coulomb force.
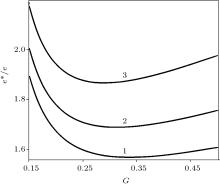 | Fig. 2. Ratios of the effective (renormalized) ion charge to the “ bare” charge versus G. The governing parameter of OSL G = Gi (for i ∈ {x, y, z}) is proportional to the intensity of the “ far-off-resonant” field, which is in accordance with Eq. (16). The governing parameter of OSL χ is proportional to the intensity of the resonant field E′ , χ = 0.07 (line 1), χ = 0.06 (line 2), χ = 0.05 (line 3). The OSL and ion parameters are 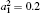 |
The equations of the force balance (compared with Eq. (1)) should be rewritten as follows:
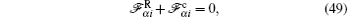
where α ∈ {1, 2}, i ∈ {x, y, z}. According to Ref. [4], we introduce relative and center-of-mass coordinates {η } → {η 1} = (r, R):
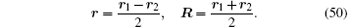
For certainty, the situation is considered when two ions are located in the same OSL unit cell Ω 0, with the center of the cell Ω 0 coinciding with the origin of coordinates. Then, the equilibrium (metastable) configurations 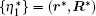
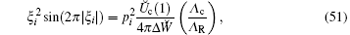

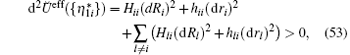
where 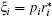

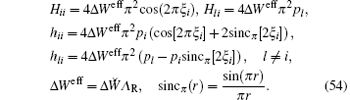
Inequality (53) implies that the second differential of Ŭ eff({η 1}) at the point 
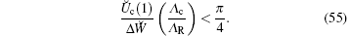
Indeed, in this case there is the positive root ξ * < 1/4 of Eq. ( 51) for i = x (px = 1) and the elements of the Hessian matrix are positive (Hxx, Hlx, hxx, hlx > 0, l ∈ {y, z}), i.e., condition (53) is satisfied. When inequality (48) is satisfied, condition (55) is transformed into earlier obtained condition (3).[4] It follows from Eq. (55) that the formation of the two-ion cluster is only possible in the case where the period of OSL exceeds the critical length (L > Lcr) at which 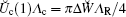
It is easily understood if it is taken into account that Ŭ c(1) ∝ 1/L and 
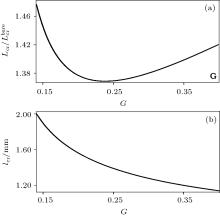 | Fig. 3. (a) The ratio of the normalized critical OSL period Lcr to the critical OSL period 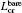 |
The condition analogous to inequality (4) for the renormalized model is modified to the following inequality:
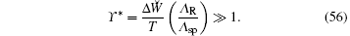
Inequality (56) provides a possibility of forming a long-lived two-ion cluster with the lifetime τ ∼ τ M ≫ τ cl, where τ cl is the characteristic time of the cluster formation.[4] Besides, from inequality (56) it follows that at time τ ≫ τ cl the fluctuations of the ions about their equilibrium positions are small as compared with the dimensionless cluster size 2ξ * .
Now we consider the last question in more detail. To be more exact, we are to investigate the dynamics of the fluctuations of ions about their equilibrium positions corresponding to x-configuration with py = pz > 1. The linear approximation of Eq. ( 45) can be written in the compact matrix form
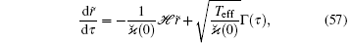
where ℋ is the diagonal Hessian matrix (ℋ = Diag(hxx, hxy, hxz, Hxx, Hxy, Hxz)) which is defined by Eq. (54) with i = x, py = pz = p > px = 1, r̃ is the column vector, r̃ = col(r̃ x, ry, rz, Rx, Ry, Rz), r̃ x = rx − ξ * , and ξ * is the positive root of Eq. (51) for i = x,
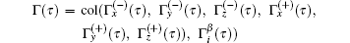
is the Gaussian white noise (i ∈ {x, y, z}, β ∈ {+ , − }) and correlator 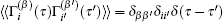
Equation (57) can be used for the time shorter than the characteristic lifetime of the ion cluster τ M, whose finiteness is due to the manifestation of the large rare fluctuations, [22] i.e., the cluster metastability. This equation leads to the estimation of the characteristic formation time of the cluster 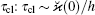
In particular, the following important relations are obtained:
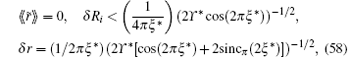
where δ r = σ {| r| }/2ξ * and δ Ri = σ {Ri}/2ξ * are the values characterizing the relative level of fluctuations (which is compared with the size of the cluster 2ξ * ), the interionic distance, and CM position. These fluctuations are suppressed when the parameter ϒ * increases. Figure 4 shows the characteristic scale of the value of ϒ * for certain values of the OSL parameters. For the parameters in Fig. 4 the δ r and δ Ri are about 0.07, temperature T ≈ 0.3, 8.5 > 𝒜 > 2.65 and the coupling parameters, Γ c, 
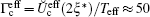
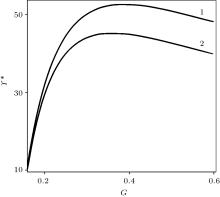 | Fig. 4. The parameter ϒ * versus the governing parameter of OSL G. The value of ξ * is fixed to be equal to 0.18, the governing parameter of OSL χ = 0.07 (line 1), χ = 0.0.5 (line 2). All the other parameters are the same those as in Fig. 2. |
This example demonstrates a real possibility to satisfy all the formation conditions of the two-ion (Coulomb) cluster in OSL in the case where the SI approximation (inequality (5)) is not applicable and one has to use the renormalized model constructed in the present work.
It is shown that in order to correctly formulate the conditions for the formation of the two-ion (Coulomb) cluster in the 3D polychromatic dissipative superlattice cell, suitable renormalization of the optical and Coulomb force terms in the force balance equation is necessary. Such a renormalization allows one to take into account the important factor of the nonlinear dependence of the optical forces on the velocity and, the strongly non-Maxwellian (Tsallis type) characteristic of the velocity distribution of ions in OSL.
The renormalization effects are most significant for the case of weak light fields, where the lowest (sub-Doppler) temperatures of ions are reached. In this case the effective charge e* (which determines the renormalized Coulomb ion– ion interaction) is a function of OSL governing parameters, G and χ , and always exceeds the value of the “ bare” ion charge. The consequence of this circumstance is the increase of the critical (minimal) period of the OSL at which the effect of the two-ion cluster formation is achieved.
Another important result of the present work which has stand-alone value, is the derivation of a closed system of stochastic differential equations describing the light-induced Brownian motion of ions in the configuration space (r1, r2). This system of reduced Langevin equations with additive noises is considerably simpler than the original system of the Langevin equations with multiplicative noises. Using these equations to describe the ion dynamics in OSL is not limited to the narrow frames of the slow ion approximation[9] and allows implementing the numerical simulations of the long-time dynamics of the ions for much longer time than in Ref. [4]. This is extremely important for the investigation of the dependence of the cluster life-time on the OSL parameters. The cluster life-time is determined by the rare large fluctuations, thus, its accurate calculation requires carrying out simulations in long-time intervals.
In conclusion, it may be suggested that the considered effect of renormalization of the Coulomb interaction should be used in problems of the optical creation and confinement of ultracold electron– ion plasma.[8]
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|


