†Corresponding author. E-mail: chenxm@lzu.edu.cn
*Project supported by the National Natural Science Foundation of China (Grant Nos. 11174116 and 11175075).
The values of cross-section ratio R k1 of direct k-fold ionization cross section ( σ k) to direct single ionization cross section ( σ1) of Ne impacted by C q+ ( q = 1–3) ions in an energy range of 10 keV/u–500 keV/u are measured in this work. The experimental data are compared with the results from our multi-electron classical over-barrier ionization (ME-COBI) model, showing that the model can give a good estimate to the experimental data.
The study of the multiple ionization of atoms is a research hotspot of atomic and molecular physics. This research can provide important evidence for astrophysics, plasma physics, cluster physics, and many other technological areas.
The collisions between atoms and ions have been studied extensively at projectile velocities vp in the case of either very low[1, 2] (vp≪ v0) or very high[3, 4] (vp ≫ v0) compared with Bohr velocity v0. At the low velocity, the process can be understood well in the framework of Bohr’ s classical over barrier model (COBM).[5] In this model, the capture process is dominant and the direct ionization can be ignored. The cross section of capture is independent of the projectile velocity vp, as a result, the ratio of the multiple ionization to the direct single ionization can be expected to be a constant. The ionization process becomes a dominant process at high velocities. Much theoretical work is available on the high energy ionization problem, such as the plane wave Born approximation (PWBA), [6] first-order semi-classical approximation (SCA), [7] statistical energy deposition (SED) model, [8] and continuum distorted wave-eikonal initial state (CDW-EIS) approximation.[9]
As a simple two-electron system, the ionization of He is widely studied both theoretically and experimentally.[10– 17] In a low-to-intermediate energy range, our previous work based on the classical over-barrier ionization (COBI) gave a good description for the direct ionization of He.[18]
For the more complex systems, Ding et al.[19] investigated the L-shell ionization process of Ne associated with single-electron capture by Cq+ (q = 2, 3) using the projectile-recoil-ion coincidence method. Wolff et al.[20] presented measurements of absolute cross sections for the single-electron loss for B2+ by Ne and Ar targets, and for C3+ by Ar targets. But for the multiple ionizations of many electron targets, such as Ne, the understanding of the direct ionization is still not enough.
In the present work, Cq+ (q = 1– 3) with the low to intermediate collision velocity region collide with Ne. We discuss our experimental data based on our ME-COBI model.[21] The values of multiply-to-single ionization ratio Rk1 of Ne are measured using the time-of-flight and coincidences technique, and the results are compared with the theoretical estimates. The aim of the present work is to add knowledge about direct multiple ionization in ion– atom collision in a low-to-intermediate collision velocity range.
The experiment is conducted using the 2 × 1.7-MV tandem accelerator of Lanzhou University. Ions provided by a sputtering ion source were accelerated in the accelerating tube and were selected by a 30° -magnet. The selected Cq+ beams were collimated by two sets of adjustable slits and well defined in size smaller than 0.25 mm × 0.25 mm. The energetic ions with charge state q collided with the gas target atoms, which were introduced into the collision region through a pen value, in the target chamber. The pressure was adjusted to ensure single ion– atom collision conditions in the experiments. In the work, the background pressure was less than 8 × 10− 6 Pa, and the working pressure in the target cell contained was ∼ 2 × 10− 3 Pa. The scattered projectiles, which might or might not change their charge states during collisions, entered into a parallel plate electrostatic charge analyzer. Various charge states of the scattered projectiles were separated and detected by a position-sensitive micro-channel plate detector (PSMCP). Target recoil ions produced from collisions with projectile ions were extracted by a static electric field (500 V· cm− 1). Coincidences between Ne recoil ions and outgoing projectiles were recorded by a time-to-amplitude converter (TAC). The recoil charge states were identified from the difference in time of flight (TOF) between recoil ions. We can identify each individual process in ion– atom collisions from the relevant coincidence spectrum between the recoil time of flight and projectile position. In direct ionization, the projectile does not change its charge state during the collision. The Ne atom may lose one electron (the cross section is denoted as σ + ) or lose more than one electron (denoted as σ k+ ). In this case, the ratio Rk1 could be determined by
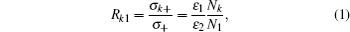
where Nk and N1 are the numbers of the detected Nek+ and Ne+ events undergoing no charge exchange, and ɛ 1 and ɛ 2 are the detection efficiencies of Ne+ and Nek+ . The main uncertainty in the coincidence measurements come from the determination of the detection efficiencies (about 10% ), statistical errors and random coincidence (typically < 15% ).
Our ME-COBI model is based on COBI[22– 26] and the over barrier (OB) models.[5] According to the capture model of OB, one electron can be released from the target atom when the Coulomb force is lower than the binding force of the electron in the atom. The released distance Rr is given by

where Z and q are the effective charges of the target core and the projectile respectively, I is the electron binding energy of the target atom.
The capture occurs when the release occurs within the capture distance Rc, and the electron’ s potential energy is larger than its kinetic energy in the projectile frame. The capture distance is determined by Rc = 2q/v2, where v is the projectile’ s velocity.
The OB model does not describe the electron released outside the capture distance Rc. When the release occurs outside the capture distance, it will not be ionized until it obtains enough kinetic energy to escape. When the kinetic energy of the released electron covered from the Stark energy is larger than its binding energy, then the ionization takes place. So the ionization distance RI satisfies the inequality:
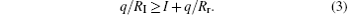
For the release, the capture and ionization proceed gradually. Here the corresponding one-electron probabilities Pr, Pc, and PI for release, capture, and ionization are used, which are given by

where b is the collision parameter and T is the orbital period of the target electron.
In this model, we use the one-electron ionization probability to construct the relevant multi-electron ionization probability within the framework of the independent-particle model (IPM).[27]Rrk, Rck, and RIk are the release, capture, and ionization distances for the k-th released target electron. They satisfy the following equations:
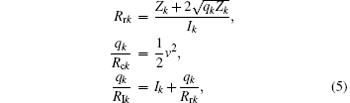
where Zk and qk are the charges of the target and the projectile seen by the k-th target electron. The values of qk and Zk are determined by the method adopted by Niehaus in the molecular Coulomb over barrier model (MCOBM).[28]
The value of the ionization probability PIk can be calculated by RIk. So the relevant k-fold ionization probability is
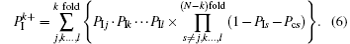
By using the equation, we can calculate the k-fold ionization cross section (σ k + ) of an atom as
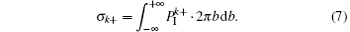
Then we will obtain the ratio

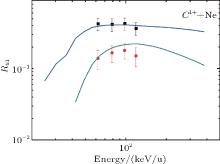
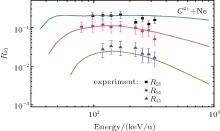
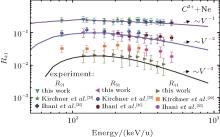
Figures 2– 4 show our measured values of cross section ratio Rk1 for Cq+ – Ne (q = 1– 3), the estimates from the present theory, and previous other groups’ results.[29, 30]
 | Fig. 3. Ratios of DMI to DSI of C2+ versus projectile energy. Solid line is the present theoretical estimate. |
 | Fig. 4. Ratios of DMI to DSI of C3+ versus projectile energy. The solid line is the present theoretical estimate. |
It is clear that our experimental data and other groups’ results are quantitatively accordant with the present results for R21 and R31 obtained from the ME-COBI model, and for R41, they are qualitatively consistent with the result from the present model. The experiment and the theory model both indicate that the cross section ratios for Cq+ – Ne collision are strongly dependent on projectile energy. The ratios increase at the energy under 100 keV/u, reach the maximum values in a range of about 50 keV/u– 200 keV/u, and then decrease.
To understand the result, we analyze the ionization probability for the impact parameter b = 0. The ionization cross section is given by[24, 26]
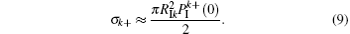
From the above Eq. (6), where we have expressions PIj = 2 · (Rrj − Rcj)/Tv and 1 − PIs − Pcs = 1 − Prs, we can then obtain
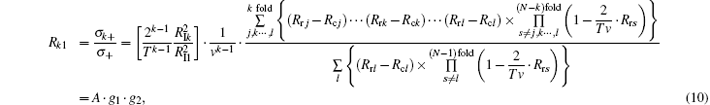
where
From Eq. (5), because Rrk and RIk are independent of v, A is also independent of v.
The value of g1 decreases with the increase of v. Because the probability cannot be negative, Rrj − 2qj/v2 > 0, we can obtain B − C/v2 > 0. The value of g2 increases with the increase of v. With the competition between g1 and g2, the cross section ratios increase at the lower energies, and a maximum value appears in a low-to-intermediate energy range, then decreases at higher energies.
For energy being larger than 200 keV/u,
g2 can be approximated to being independent of v. We can obtain the ratio Rk1 for higher energies as follows:

When the projectile energy is larger than 200 keV/u, the results from the present model and the experiments both show the ratio drops off approximately as v− (k− 1). Such an energy dependence is quite different from the binary-encounter laws of v− 2(k− 1), [31] which is valid for the fast ion– atom collision.
In a low-to-intermediate energy range (tens-to-hundreds of keV/u), the collision velocity is comparable to the orbital velocity of the target electron, and the target electrons have enough time to pass through the Coulomb barrier. Therefore the over-barrier ionization process is considered to be the main ionization mechanism for the low-to-intermediate energy range.
For projectile energy in an MeV/u energy range, the release probability is too small to let the over-barrier ionization mechanism be dominant. When violent binary-encounters between projectile and target electrons start to play an important role, it determines that the ionization obeys the v− 2(k− 1) law.
Therefore, the ME-COBI model which considers the over-barrier ionization process, but ignores the binary-encounters will be good in a low-to-intermediate energy range, and be somehow limited for higher energy range.
For energy larger than 200 keV/u, from the present model we can obtain the following equations:
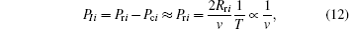
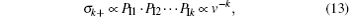
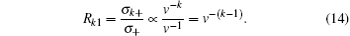
Because the experimental data decrease with energy, which has nearly the same trends that the present model has, the multiple ionization mechanism of neon can be regarded as sequential over-barrier ionizations. With the projectile approach, the target electrons will be released one after the other to the side of the projectile. When they enter into the ionization distances, these electrons will be ionized out one by one.
In the present work, we measured the multiple ionization of neon induced by 10 keV/u– 500 keV/u Cq + (q = 1– 3) ions. We also use our theoretical model to estimate the ratios, and find that they are in good agreement with our and other people’ s experimental data. It means that our ME-COBI model is useful for explaining the multiple ionization in the energies ranging from 10 keV/u to 500 keV/u.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|
| 28 |
|
| 29 |
|
| 30 |
|
| 31 |
|