Ion– atom ionizing collisions, which are of importance in atomic physics^[1] and many applications in the fields of fusion, ^[2] accelerator, ^[3] and plasma physics, ^[4] have received much attention for several decades.

On the theoretical side, there are several approaches to calculating the cross sections.^{[5– 7]} These approaches include the classical trajectory Monte Carlo (CTMC), ^[8] the classical deposition models like the DEPOSIT code, ^[9] and quantum-mechanical calculations based on the first-order perturbation theory.^{[10– 15]} The ionizations of noble atoms impacted by a projectile at high and low energies have already been understood well both in theory and in experiment.^{[12, 16– 20]} In low energy range (E < 10  keV/amu, amu is the abbreviation for atomic unit per nucleon), the collision is adiabatic and the electron circulates many times around both nuclei. The electron energy in such a ‘ quasi-molecule’ is determined as a function of the inter-nuclear distance R. Adiabatic approximation such as the well-known over-barrier (OB) model proposed by Bohr et al., ^[21] can well describe the electron capture process. The OB treatment is applicable to electron capture by the projectile, ^{[22, 23]} but is not valid for the direct ionization process.

In a high energy range (E > MeV/amu), the electron interaction with the projectile takes place within a very short time, and the first-order perturbation method is valid. Born approximation, ^{[12, 24]} Bethe formula, ^[25] and the CDW-EIS theory^[5] can be used for calculating the ionization cross sections and the comparison with available experimental data is shown in Refs.  [12] and [16]– [20]. All these theories indicate that for E > MeV/amu only collisions with sufficiently small impact parameters result in ionization, the energy is transferred to electrons via violent binary-encounters.

It is evident that the perturbation theories are not valid at strong perturbative energies (several tens to hundreds keV/amu), where the assumptions of free electron and binary encounter did not hold true. Though the calculation results given by the first principles quantum theories^{[26– 28]} are in good agreement with experimental results, the knowledge of the underlying physics of ionization is still inadequate. On the application side, a universal formula or scaling law is needed to help us to understand the experimental data. Kaganovich et al. have reviewed the process of scaling law for He target in a wide energy range, ^[16] whereas the scaling law for many kinds of noble gases in strong perturbative energy range has not been reported yet.

The aim of this work is to obtain the projectile charge q and projectile velocity v, also the dependence of single ionization cross section of the target atom, through a classical calculation for the whole set of noble gas targets. The calculated single ionization cross sections from He to Xe impacted by various projectiles at energies ranging from 10  keV/amu to 800  keV/amu are in good agreement with the experimental data. Based on the calculation model, we propose a useful scaling law of single ionization cross sections for noble gases in a strong perturbative regime. The details of the model are presented in Section 2. The calculated results are compared with experimental results and the scaling law is discussed in Section 3. The atomic unit (a.u.) is used throughout the present paper.

The model we used to calculate the single ionization cross sections of He, Ne, Ar, Kr, and Xe targets is based on our previous work of COBI^{[29– 31]} model and also on Bohr’ s OB.^[21] Now, we will review them briefly.

Two important ion– atom interaction distances are introduced in OB. The first distance is the release distance R_r, where the electron can be released from the target nucleus. The release distance R_r satisfies

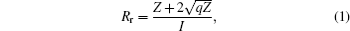
where I is the ionization energy of the target electron, q is the projectile charge, and Z is the nuclear charge of the target atom.

The second distance is the capture distance R_C, where the electron can be captured by the projectile, and it satisfies the following equation:

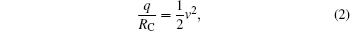
where v is the velocity of the projectile.

Equations (1) and (2) mean that only if the release occurs within the capture distance, can the released electron be captured, otherwise, the release is temporary. In OB, ^[21] the electrons which are released but not captured will go back to the target atom after collision. The energy level of the released electron has already been estimated by Bohr^[21] and Niehaus, ^[22] and it is I + q/R_r, i.e., the ionization energy of the target electron plus the Stark-energy by the ion.

In COBI, we consider that the released but not captured electrons will be accelerated by the approaching ion. At some distance R_I, the electrons will get enough kinetic energy from the ion to escape from the target atom, meanwhile, these electrons will not be captured, and they will be ionized. The ionization distance R_I satisfies

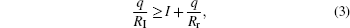
which means that when the Stark-energy transferred to the kinetic energy of the electron is larger than the ionization energy of the quasi-molecular states, the electron will escape from the target atom. If it is not captured, it will be ionized. That is, in our model, the electrons released within the distance R_C will be captured; those released electrons between R_r and R_C will not be ionized until the ion enters the distance R_I. For the given collision parameter b and velocity v, the probability that the electron will be released is

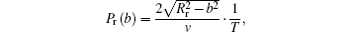
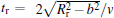
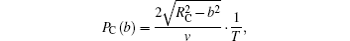
i.e., the ratio of collision duration of release process to the period of the bound electron T = 2π · n³/Z², for b ≤ R_r. The capture probability is

i.e., the ratio of collision duration of capture process 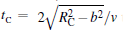to the period of the bound electron T, for b ≤ R_C. Then, the ionization probability is P_I (b) = P_r (b) − P_C (b), for b ≤ R_I.

Multiple electron probability will be extracted from these one-electron probabilities by using the independent event model (IEVM). For a multi-electron target, it has been found that IEVM is more adequate^{[32, 33]} than the independent particle model (IPM). IPM ignores the variation of considerable ionization potential with the charge state, which leads to wrong probabilities for the high stages of ionization.

Fig.  1.

	Figure Option ViewDownloadNew Window
	Fig.  1. Single ionization cross sections of He target impacted by various heavy ions. Lines represent calculation results and dots refer to experimental data.[27, 34– 41]

When we construct the cross section of a multi-electron system, it is necessary to distinguish these electrons with subscript i. They satisfy the following equations:

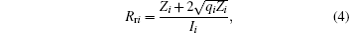
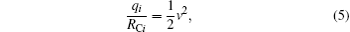
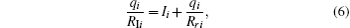
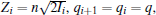
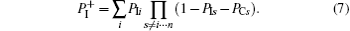
where q_i and Z_i are the effective charges of the incident ion and the target, felt by the i-th released electron of the target. for the released electron loses the ability to shield target and projectile nucleus. The values of P_Ci (b) and P_Ii (b) are calculated from R_ri, R_Ci, and R_Ii. With the statistical method of multinomial distribution, the related single ionization probability can be obtained as

The cross section is obtained by integrating the probability over all impact parameters and expressed as

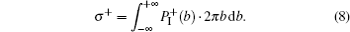
The calculation results are plotted in Fig.  1 together with the experimental data within the same energy range.

We calculate the single ion– atom impact ionization cross sections of He impacted by various kinds of heavy ions in the energy range from tens to hundreds keV/amu. The calculation results are shown in Figs.  1 and 2 and compared with extensive experimental data. It is clear that the model results are in good agreement with the experimental data.

Fig.  2.

	Figure Option ViewDownloadNew Window
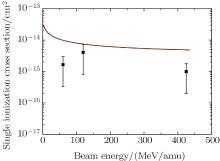	Fig.  2. Single ionization cross section of He target impacted by U90+ , the solid line represents the calculation results and square dots refer to experimental data.[42]

The model well describes the q- and E-dependent single ionization cross sections. The calculation results and the data both show that (i) the single ionization cross sections of helium increase very rapidly at low energies (below about 100  keV/amu) and reach their maxima at energies ranging from 100  keV/amu to 400  keV/amu, and then drop off very slowly at higher energies; (ii) the maximal ionization cross sections increase significantly with the increase of projectile charge q, while the maximum positions increase with q slightly.

The behavior of single ionization cross section on q and E can be understood qualitatively by the model, for the dependence of the single ionization cross section on q and E is similar to that of the single ionization probability P_I, and we will discuss the ionization probability P_I(0) at b = 0.

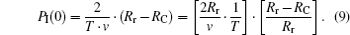
Let h = (2R_r)/v · 1/T and g = (R_r − R_C)/R_r, where h is the ratio of collision duration 2R_r/v to the period T of the target electron. Obviously, h is the release probability during the collision, and it is equal to the unity at low energies and decreases according to 1/v for high energies. g is the uncaptured fraction of the released electrons, g = 1 − (2q/R_r) · (1/v²), which increases strongly according to v² and is close to the unity for high v.

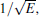
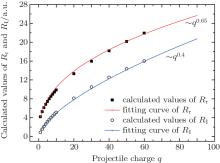
The uncaptured fraction of the released electrons g increases according to v²; this is the main reason for the increase of ionization cross sections at low energies. The interaction time h decreases according to causing the ionization cross sections to decrease very slowly for high energies. At intermediate energies, the uncaptured fraction g increases while the interaction time h decreases. The competition between them leads to the occurrance of maximum ionization cross sections.

Moreover, capture and ionization are both dependent on the projectile charge. However, increasing collision velocity reduces the capture cross section more rapidly than the ionization cross section. In order to reduce the capture cross section, the effect of collision velocity must overcome the capture process, which means that higher and higher velocities are needed for a significant ionization contribution when the projectile charge state is increased. This is the reason why the ionization cross section maximum shifts toward higher velocities for higher projectile charges. Approximately, the maximum position, where the maximum ionization cross section is reached, can be obtained by setting the derivative of Eq.  (7) to be zero. The estimated maximum position E_max is found to be proportional to 6q/R_r. In our calculation, we find that the values of R_r can be fitted well by the curve of q^0.4 (see Fig.  3). Thus, the maximum position will show the q^0.6 dependence. This is why the maximum position of E_max does not vary significantly with q.

Fig.  3.

	Figure Option ViewDownloadNew Window
	Fig.  3. Calculation results of Rr and RI and their fitting curves.

On the other hand, the maximum ionization cross section is shown to strongly increase with q. According to Eq.  (3), the maximum ionization cross section can be estimated roughly at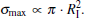 The calculation result of R_I shows the q^0.65 dependence (see Fig.  3). So, we can expect that the maximum ionization cross section will be dependent on q in the form of about q^1.3.

In order to obtain the target dependence of the single ionization cross section, we calculate the single ionization cross section of noble gases ranging from He to Xe impacted by He⁺ ion. The calculated results are shown in Fig.  4 and compared with the available experimental data. We can see that the model gives good estimation to the experimental data. Based on the present model, we can estimate the target dependence of the maximum ionization cross section qualitatively. According to Eq.  (3), the dependence of R_I on target ionization energy I is 1/I, and then the maximum ionization cross sections of different targets will show the (1/I)² dependence.

Fig.  4.

	Figure Option ViewDownloadNew Window
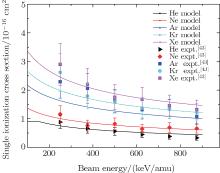	Fig.  4. Single ionization cross sections of noble gases from He to Xe impacted by He+ ion. Lines represent the calculation results and dots refer to the experimental data.[43]

Now, we suggest that the q, v, and I dependences of the maximum ionization cross section are σ _max ∝ q^1.3/I² and E_max ∝ q^0.6. Based on such dependences, we can obtain a scaling law of the single ionization cross sections of noble gases. As a result, the single ionization cross section of a target X having the first ionization energy I and being impacted by a projectile with charge q and energy E can be estimated by

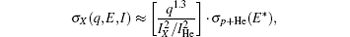
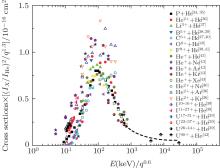
and E* ≈ E · q^0.6. For clarifying the validity of such a scaling law drawn from the model, we scale the single ionization cross sections of the whole set of noble gases impacted by various kinds of heavy ions in Fig.  5. In this figure, we can find that the extensive experimental data can be fitted well by the scaling law. This scaling law builds a convenient connection between the usual proton data and other data for different collision systems at energies ranging from tens to hundreds keV/amu.

Fig.  5.

	Figure Option ViewDownloadNew Window
	Fig.  5. Scaled single ionization cross sections of noble gases ranging from He to Xe impacted by various kinds of heavy ions.[27, 34– 43] The dashed line is used only to guide the eyes.

The single ionization cross sections of noble gases ranging from He to Xe, are calculated at strong perturbative energies. The calculation results are in good agreement with the extensive experimental data. Based on the model, the scaling law is drawn to describe the q, E, and I dependences of single ionization cross sections at such energies. It is found that the extensive experimental data can be fitted well by the scaling law of

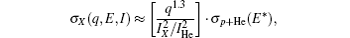
and E* ≈ E · q^0.6. This work provides a convenient way to estimate the single ionization cross sections of noble gas targets impacted by various kinds of heavy ions from the easily obtained proton data.